【応用】通過領域(縦に切る)
ここでは、直線が動いたときに、その直線が通過する領域を求める問題を考えます。解き方は複数ありますが、縦に切って考える方法を見ていきます。
通過領域
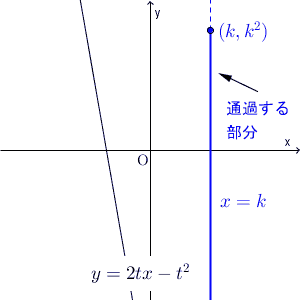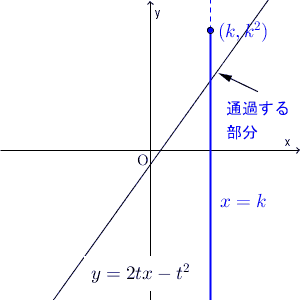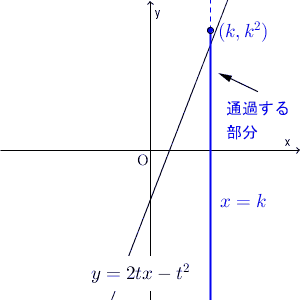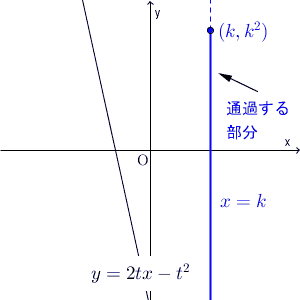
t が動くと、直線 $y=2tx-t^2$ は次のように動きます。
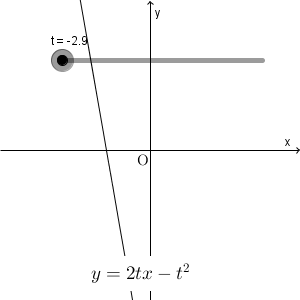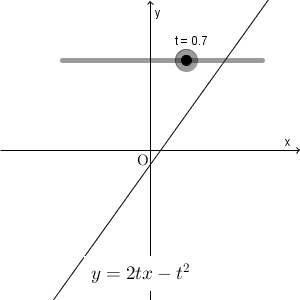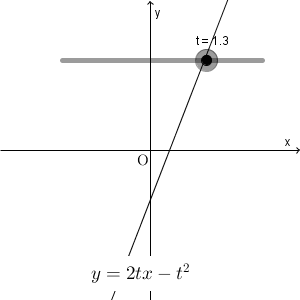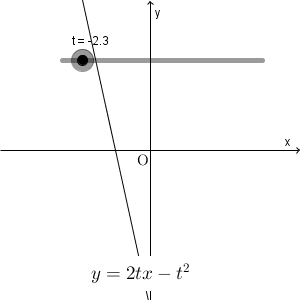
この直線が通る領域を求める問題です。
直線はいろいろ動くので、直線だけを見ていても、通過する領域を求めることは難しいです。ここは、【基本】直線と領域で見たように、 $x=k$ で切って考えます。
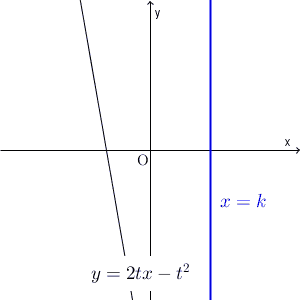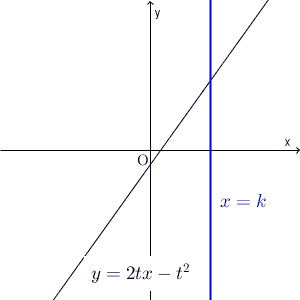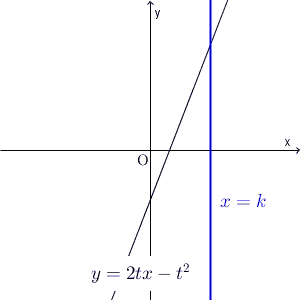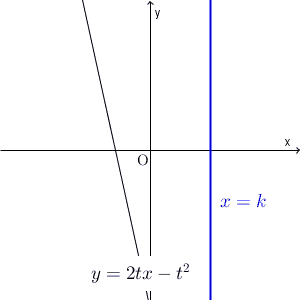
直線 $x=k$ と、直線 $y=2tx-t^2$ との交点に注目します。このとき、交点が、直線 $x=k$ のどの部分を動くか、を考えます。それを全体に広げれば、通過する領域がわかる、という流れです。つまり、通過する領域を縦に切って求める、ということです。
さて、 $x=k$ のとき、交点がどう動くかを考えましょう。 x を固定するので、 t が動くときに、変化するのは y だけです。 y の値がどう変化するかを見ればいいですね。
\begin{eqnarray}
y
&=&
2tk-t^2 \\[5pt]
&=&
-(t-k)^2+k^2
\end{eqnarray}と変形できます。 t はすべての実数値をとるので、 y は $k^2$ 以下のすべての値をとることがわかります。
通過する領域を、直線 $x=k$ で切ると、 $y\leqq k^2$ の部分が該当箇所だ、ということがわかります。
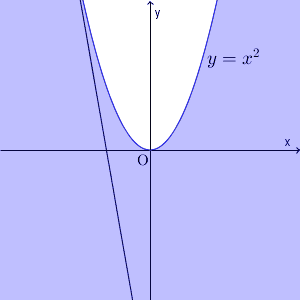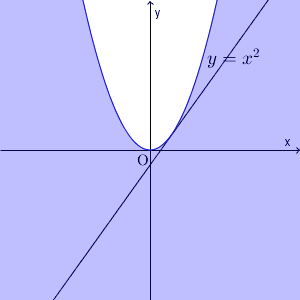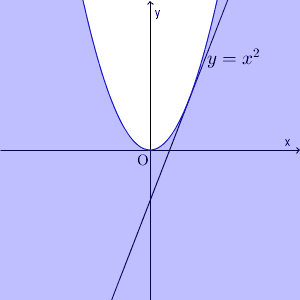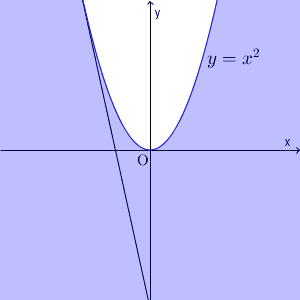
このことから、求める領域は、図の色のついた部分(境界線上の点を含む)となります。
通過領域その2
先ほどと直線の式は同じですが、 t の動く範囲が限られています。なので、答えは先ほどの領域に含まれる一部分だということがわかりますね。
先ほどと同じように考えていきましょう。 $x=k$ として、 y の取りうる値を考えます。
\begin{eqnarray}
y
&=&
2tk-t^2 \\[5pt]
&=&
-(t-k)^2+k^2
\end{eqnarray}と変形できるところまでは同じですが、これから「 y の取りうる値は $k^2$ 以下だ」とは言えない点に注意しましょう。例えば、 $x=k=2$ とすると、 $y=2^2$ となるのは $t=2$ のときです。しかし、今の t の範囲は $t \leqq 1$ なので、 $t=2$ は範囲外です。つまり、 $(2,4)$ という点は通過しないのです。こうした不要な点は除かなくてはいけません。
これは、【応用】二次関数の最大・最小(軸が動く)で見た、二次関数の軸が動く場合の最大・最小を求める問題と本質的に同じ問題です。 頂点 $(k,k^2)$ が今考えている範囲に入っているかどうかで、状況が変わります。 k の値によって、最大値をとるところが違うので、場合分けをして考えていきます。
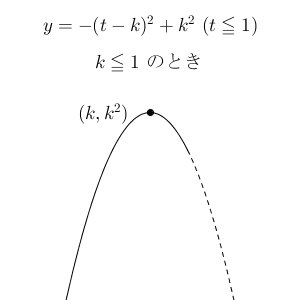
まず、 $k \leqq 1$ の場合。このときは、 $t=k$ となることができるので、 y は $k^2$ 以下のすべての値をとります。
一方、 $k\gt 1$ の場合は、頂点 $(k,k^2)$ は $t=1$ より右にあります。よって、最大となるのは、 $t=1$ のときで、そのときの値は
\begin{eqnarray}
y
&=&
2 \cdot 1 \cdot k-1^2 \\[5pt]
&=&
2k-1
\end{eqnarray}となります。
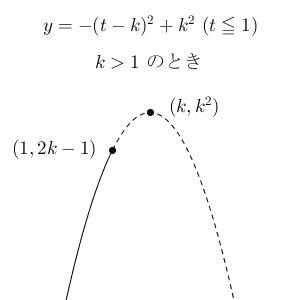
以上から、通過する領域を $x=k$ で切ると、 $k\leqq 1$ の場合は $y\leqq k^2$ の部分、 $k\gt 1$ の場合は $y\leqq 2k-1$ の部分が該当箇所だとわかるので、通過する領域は次のようになります。
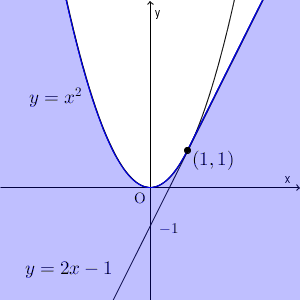
上の図の色のついた部分(境界線上の点を含む)が求める領域となります。先ほど「 $(2,4)$ は通らない」と書きましたが、実際、 $(2,4)$ は領域に含まれていないことがわかりますね。
縦に切って通過する領域を求める考え方のまとめ
注目するものが途中で変わるので、今何を考えているのか、しっかり把握しながら考えましょう。
まず、「直線が動く」というのをそのまま考えるのは難しいので、「通過する領域を縦に切って、切り口がどうなるかを考える」という発想を使います。
次に、切り口がどうなるかを考えるため、切り口の一番上の部分(最大値)と下の部分(最小値)を求めます。1つ目の例題では最大値は1パターンでしたが、2つ目の例題では、切る場所によって最大値のパターンが2つありました。切り口がどうなるかは、関数の最大値・最小値を求める問題になっています。
最後に、縦に切ったときの切り口が分かったので、それをつなぎ合わせれば、求める領域が得られる、という流れになっています。
おわりに
ここでは、動く直線が通過する領域を求める問題を考えました。縦に切って、切り口がどうなるか、に注目して考えました。出てくる関数が複数あり、最大・最小を正しく求める必要もあるため、難易度の高い問題です。





