【応用】楕円となる軌跡
🕒 2018/04/22
🔄 2023/05/01
ここでは、軌跡が楕円となるような問題を考えてみます。
📘 目次
軌跡と楕円
例題
線分 AB は長さが $7$ で、点 A は x 軸上を動き、点 B は y 軸上を動きます。このとき、線分 AB を $3:4$ に内分する点の P の軌跡を求めなさい。
まず、わかりやすいのは A, B の座標なので、これらを使って P の座標を表すことを考えましょう。
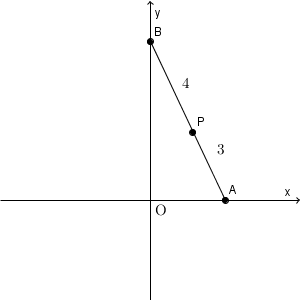
2点 A, B の座標を、それぞれ $(a,0)$, $(0,b)$ とします。長さが $7$ なので、\[ a^2+b^2=49 \]が成り立ちます。
また、点 P の座標を $(x,y)$ とすると、\[ x=\frac{4}{7}a,\ y=\frac{3}{7}b \]となります。これを変形すれば、\[ a=\frac{7}{4}x, \ b=\frac{7}{3}y \]となります。これを先ほどの式に代入すれば
\begin{eqnarray}
\left(\frac{7}{4}x\right)^2 +\left(\frac{7}{3}y\right)^2 &=& 49 \\[5pt]
\frac{1}{16}x^2 +\frac{1}{9}y^2 &=& 1 \\[5pt]
\end{eqnarray}となります。
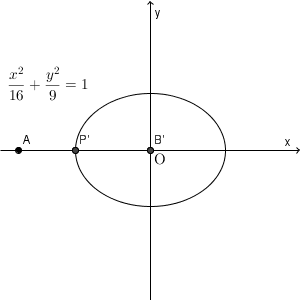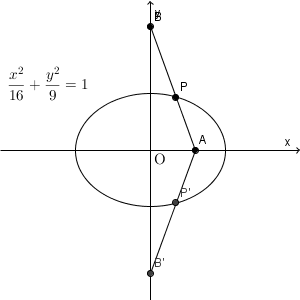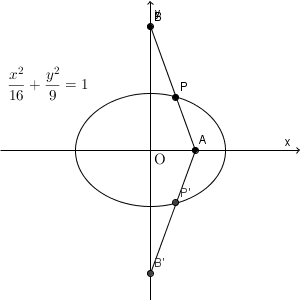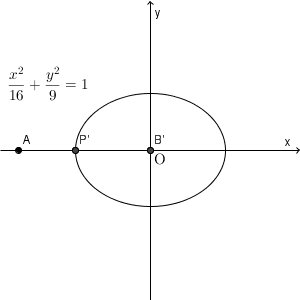
よって、点 P はこの楕円上にあり、逆に、この楕円上にある点は条件を満たすので、求める軌跡は、楕円 $\dfrac{1}{16}x^2+\dfrac{1}{9}y^2=1$ となります。
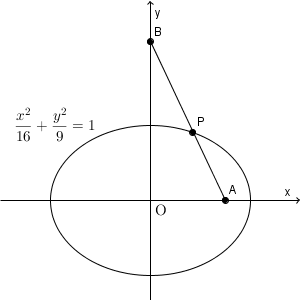
実際に、 A, B, P を動かしてみると、次のようになります。
おわりに
ここでは、軌跡が楕円となるような問題を見ました。軌跡の求め方は一般的な場合と同じですが、得られた軌跡がどういう図形かがわかるようになっておきましょう。





