【応用】積分と回転体の体積(2曲線で囲まれた部分)
ここでは、2曲線で囲まれた部分を回転させて、その体積を求める問題を考えていきます。
例題
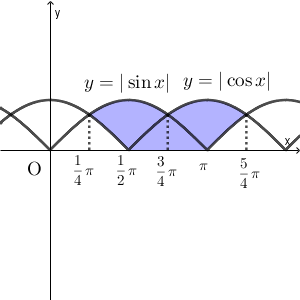
図は次のようになります(参考:【基本】2曲線間の面積と積分の復習)。

$\sin x=\cos x$ とすると、 $\sin x-\cos x=0$ であり、合成を使えば $\sqrt{2} \sin\left(x-\dfrac{\pi}{4}\right)=0$ なので、今考えている範囲では $x=\dfrac{1}{4}\pi, \dfrac{5}{4}\pi$ となるので、交点の $x$ 座標がわかります。
この青い部分を回転して、できる立体の体積を求める問題です。
回転してできる立体の体積は、断面積を積分すればいいのでした(参考:【基本】積分と回転体の体積)。今の場合、断面はどうなるでしょうか。
まず、 $\dfrac{1}{4}\pi\leqq x\leqq \dfrac{1}{2}\pi$ の範囲では、$x$ 軸に垂直な平面で切ったときの断面は、真ん中に穴が開いた円となります。外側の円の半径は $\sin x$ で、内側(穴)の円の半径は $\cos x$ となります。
問題はその後です。 $\dfrac{1}{2}\pi\leqq x\leqq \dfrac{3}{2}\pi$ の場合、 $x$ 軸の上に $y=\sin x$ があり、下に $y=\cos x$ があります。

$x$ 軸の上下に曲線があるため、回転したときに自分自身と交わってしまいます。このような場合に、断面はどうなるでしょうか。内側の部分は吸収されてしまうので、 $x$ 軸から一番遠い部分を考えればいいですね。
例えば、 $x=\dfrac{2}{3}\pi$ のとき、 $\sin x=\dfrac{\sqrt{3}}{2}$ であり、 $\cos x=-\dfrac{1}{2}$ なので、この場合は、断面は、半径 $\dfrac{\sqrt{3}}{2}$ の円になります。
ただ、このようなことを $x$ によってそれぞれ考えていくのはめんどうです。これを効率よくやるためには、回転させる図形のうち、 $x$ 軸より下にある部分を折り返して、全部 $x$ 軸の上にもってくればいいです。
こうすれば、この青い部分をそのまま1回転すればいいとわかります。もう下側と交わってしまう、ということは考えなくてもかまいません。こうなると考えやすくなりますね。
ここで、 $\dfrac{1}{4}\pi \lt x\lt \dfrac{5}{4}\pi$ の区間にできた交点の $x$ 座標を確認しておきます。これは、 $y=\sin x$ と、折り返してできた $y=-\cos x$ との交点なので、 $\sin x+\cos x=0$ を解けばいいです。再び合成を使うと $\sqrt{2} \sin\left(x+\dfrac{\pi}{4}\right)=0$ なので、 $x=\dfrac{3}{4}\pi$ だとわかります。

また、グラフからも推測できますが、囲まれた図形は $x=\dfrac{3}{4}\pi$ について対称です。これは、 $y=\sin x$ と $y=\cos x$ が同じ形( $\pi/2$ だけずらしたものなので)であることからわかります。
こうして、以下の2つの区間に分けて考え、それを2倍すればいいことがわかりました。
・$\dfrac{1}{4}\pi\leqq x\leqq \dfrac{1}{2}\pi$ のとき: 外側の円の半径は $\sin x$ で、内側(穴)の円の半径は $\cos x$
・$\dfrac{1}{2}\pi\leqq x\leqq \dfrac{3}{4}\pi$ のとき: 半径 $\sin x$ の円
それでは、体積を求めていきましょう。
$\dfrac{1}{4}\pi\leqq x\leqq \dfrac{1}{2}\pi$ のときは、外側の円の半径は $\sin x$ で、内側(穴)の円の半径は $\cos x$ なので、この部分の体積は次のようになります。
\begin{eqnarray}
& &
\pi\int_{\pi/4}^{\pi/2} (\sin^2 x-\cos^2 x) dx \\[5pt]
&=&
\pi\int_{\pi/4}^{\pi/2} (-\cos 2x) dx \\[5pt]
&=&
\pi \left[\frac{-\sin 2x}{2}\right]_{\pi/4}^{\pi/2} \\[5pt]
&=&
\frac{1}{2}\pi \\[5pt]
\end{eqnarray}
次に、$\dfrac{1}{2}\pi\leqq x\leqq \dfrac{3}{4}\pi$ のときです。この場合は、半径 $\sin x$ の円を考えればいいので
\begin{eqnarray}
& &
\pi\int_{\pi/2}^{3\pi/4} (\sin^2 x) dx \\[5pt]
&=&
\pi\int_{\pi/2}^{3\pi/4} \frac{1-\cos 2x}{2} dx \\[5pt]
&=&
\pi \left[\frac{x}{2}-\frac{\sin 2x}{4}\right]_{\pi/2}^{3\pi/4} \\[5pt]
&=&
\pi \left(\frac{3\pi}{8}-\frac{\pi}{4}\right)-\pi\left(\frac{-1-0}{4}\right) \\[5pt]
&=&
\frac{\pi^2}{8}+\frac{\pi}{4} \\[5pt]
\end{eqnarray}となります。
なので、答えは、これらの和を $2$ 倍したものだから
\begin{eqnarray}
& &
2\left( \frac{1}{2}\pi + \frac{\pi^2}{8}+\frac{\pi}{4} \right) \\[5pt]
&=&
\frac{3}{2}\pi+\frac{\pi^2}{4}
\end{eqnarray}となります。
おわりに
ここでは、2曲線で囲まれた部分を回転してできる立体の体積を求める問題を見ました。回転したときに自分自身と交わってしまう場合には、折り返して考え、断面がわかりやすくなるようにしましょう。





