【応用】立方体を6色で塗り分ける方法

ここでは、立方体を6色で塗り分ける方法の総数を数えてみます。円順列では「回転して同じものを同一視」しましたが、立方体の場合は三次元での回転を考えないといけないので、少し複雑になります。

正四面体を4色で塗る

まずは、正四面体を4色で塗る方法を見てみましょう。

【標準】円形に並べる（円順列）で見たように、円順列は「グルグルと回転して同じになるものを同一視」しました。ここでは、その立体バージョンです。

円順列での数え方は、2つ紹介しました。1つは、「1列に並べてから円形に並べ、回転して同じになるものを同一視する」という数え方。そして、もう1つは「回転しないように、基準をどこか1つ決めてから数える」という数え方です。これらがこの例題で使えないか考えてみましょう。

1つ目の数え方は、この問題ではあまり使い勝手がよくありません。というのも、パッと見て「回転して同じになるかどうか」がわかりにくいからです。例えば、次のような4つの塗り方のうち、回転させて同じになるものはどれでしょうか。

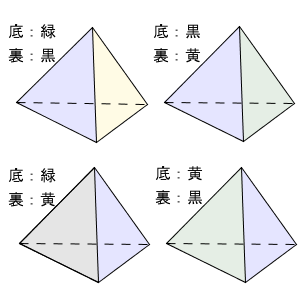
円に並べるときと違って、三次元での回転は複雑です。そのため、「塗ってから、回転させて同じになるものを同一視する」というのは、少し難しいです。ちなみに、上の4つの塗り方は、回転するとすべて同じになります。

このことから、「基準を決めてから数える」方針を考えてみましょう。どの面でもいいのですが、青い面を固定しましょう。青い面を底面にして、残りの3つの面を塗ることを考えてみます。この正四面体を上から見ると、次のようになります。

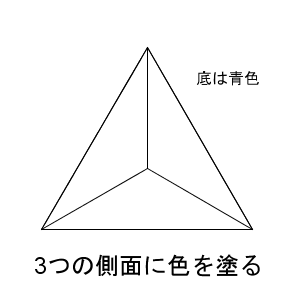
これは、実質的に、円順列と同じですね。3色を並べ、（底面を固定したまま）回転して同じになるものを同一視する、という方法で数えられます。よって\[ (3-1)!=2 \]通りだとわかります。

どんな塗り方でも、青い面があるので、その面を底にする。すると、残りの3つの面は、円順列と同じになる。こうして塗り方を数えることができました。

立方体を6色で塗る

続いて立方体です。こちらはもう少し複雑です。

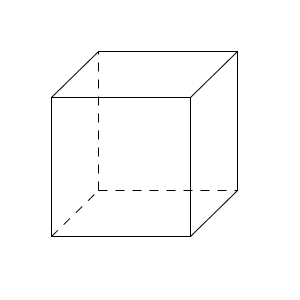
この場合も、「回転させて同じになるものを同一視する」ではなく、「どこか基準を決めてから数える」としたほうがいいです。

どのように塗っても、どこかに青色の面があるので、これを一番上の面だとしましょう。上の面を青色としてから、他の色を塗ることを考えましょう。

上の面を青色としても、側面はクルクル回転できます。しかし、底の面は固定されていますね。ということは、例えば、底の面が黄色の場合と赤色の場合とでは、回転させて同じになるものは含まれないことになります。底の面の塗り方は、青以外の5通りあり、回転させて同じになることはありません。

次に、側面の塗り方を考えましょう。これも、上から見ると、実は円順列と同じ構造になっています。

残っている4色で側面を塗り、上面と底面を固定したまま回転させて同じになるものを同一視すると、側面の塗り方は $(4-1)!$ 通りとなります。

上面を青色に固定し、底面の塗り方が5通り、そのそれぞれに対して、側面の塗り方が $3!$ 通りあるので\[ 5\times 3! = 30 \]通りが求める塗り方の総数、となります。

おわりに

ここでは、正四面体、立方体の各面を、すべて違う色で塗る方法を数える問題を見てきました。立体の場合は、「回転して同じになるか」の判断が難しいため、「どこかを固定して数える」方が考えやすくなりました。いろんな見方で数えられるようになりましょう。