【応用】座標と三角形の面積

🕒 2017/08/02 🔄 2023/05/01

ここでは、点と直線との距離を用いて、三角形の面積について考えます。

📘 目次

三角形の面積

座標を用いて、三角形の面積を求めてみましょう。

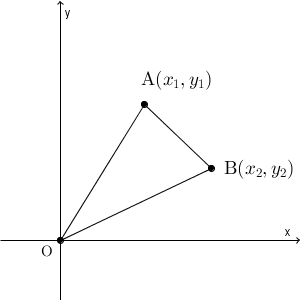
三角形の頂点が与えられたとして、その面積を求めてみます。平行移動をしても面積は変わらないので、どこか1つの頂点が原点に来るようにしましょう。平行移動後の3つの頂点を $\mathrm{ O }(0,0)$, $\mathrm{ A }(x_1,y_1)$, $\mathrm{ B }(x_2,y_2)$ とします。回転をしたあとの点の座標を求めることは難しいので、回転はせずに考えます。

さて、この三角形 OAB の面積を考えましょう。三角形の面積は、底辺×高さ÷2、でしたね。AB を底辺と考えれば、底辺の長さは\[ \mathrm{ AB }=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \]と計算できます。続いて高さですが、これは原点から AB へ引いた垂線の長さ、つまり、原点と直線 AB との距離ですね。【基本】原点と直線との距離で見た内容が使えますね。

まずは、直線 AB の方程式を求める必要があります。これは、【基本】ある2点を通る直線の方程式で見た内容が使えます。これより、
\begin{eqnarray} (y_2-y_1)(x-x_1)-(x_2-x_1)(y-y_1) &=& 0 \\[5pt] (y_2-y_1)x-(x_2-x_1)y-(x_1y_2-x_2y_1) &=& 0 \\[5pt] \end{eqnarray}となります。これと原点と直線との距離の公式から、三角形の高さは \begin{eqnarray} \frac{|x_1y_2-x_2y_1|}{\sqrt{(y_2-y_1)^2+(x_2-x_1)^2} } \end{eqnarray}となります。よく見ると、この式の分母は、 AB の長さと同じですね。このことから、三角形 OAB の面積は \begin{eqnarray} & & \frac{1}{2} \times \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \times \frac{|x_1y_2-x_2y_1|}{\sqrt{(y_2-y_1)^2+(x_2-x_1)^2} } \\[5pt] &=& \frac{1}{2} |x_1y_2-x_2y_1| \end{eqnarray}となります。シンプルな式ですね。座標 $(x_1,y_1)$, $(x_2,y_2)$ の外側同士、内側同士を掛けて引いたものが絶対値の中に入っています。

三角形の面積（座標バージョン）

$\mathrm{ O }(0,0)$, $\mathrm{ A }(x_1,y_1)$, $\mathrm{ B }(x_2,y_2)$ のとき、三角形 OAB の面積は次の式で求められる。\[\frac{1}{2} |x_1y_2-x_2y_1|\]

例えば、 $(1,2)$, $(3,5)$, $(4,1)$ という3点を結んでできる三角形の面積なら、1つ目の頂点が原点に来るように平行移動して、 $(0,0)$, $(2,3)$, $(3,-1)$ で考えて\[ \frac{1}{2}|2\cdot(-1)-3\cdot3|=\frac{11}{2} \]と求められます。

図形的な意味について

先ほどの三角形の面積の公式を、特殊な状況で見ながら、図形的な意味を考えてみましょう。

上のような状況、つまり、 $x_1\lt x_2$, $y_1 \gt y_2$ で考えてみましょう。このとき、この三角形の面積を求めるには、もちろん、先ほど見た公式が使えるのですが、もしこの公式を知らなければどうやって出すでしょうか。一番単純なやり方は、次のように四角形から不要な部分をひいていくやり方だと思います。

まず、外側の長方形の面積は、 $x_2y_1$ となります。また、左と下にある三角形の面積は、それぞれ、 $\dfrac{1}{2}x_1y_1$, $\dfrac{1}{2}x_2y_2$ となります。また、右上の三角形の面積は、 $\dfrac{1}{2}(x_2-x_1)(y_1-y_2)$ となるので、三角形 OAB の面積は
\begin{eqnarray} & & x_2y_1-\frac{1}{2}x_1y_1-\frac{1}{2}x_2y_2 \\ & & -\frac{1}{2}(x_2-x_1)(y_1-y_2) \\[5pt] &=& x_2y_1-\frac{1}{2}x_1y_1-\frac{1}{2}x_2y_2 \\ & & -\frac{1}{2}(x_2y_1-x_2y_2-x_1y_1+x_1y_2) \\[5pt] &=& x_2y_1 -\frac{1}{2}(x_2y_1+x_1y_2) \\[5pt] &=& \frac{1}{2}(x_2y_1-x_1y_2) \\[5pt] \end{eqnarray}となります。これは、先ほど見た三角形の面積の公式で絶対値をとった形になっています。

これは特殊な事例（A が B より上で、左にある場合）しか考えていないので正確な証明にはなっていませんが、先ほど見た三角形の面積の公式は、「長方形から不要な三角形を取り除いたもの」に関連していることがわかりますね。