【競プロ】余りの計算
余りに関係する計算は、競プロではよく出てきます。問題文にも「 $10^9+7$ で割った余りを求めなさい」という文言が頻繁に出てきます。ここでは、余りに関する計算方法についてみていきます。競プロ 記事の一覧はこちら。
和と余り
$13,9$ をそれぞれ $5$ で割った余りを考えましょう(参考:整数の割り算)。図を使えば、次のように、13個の丸と9個の丸を、5個ずつ、箱に分けていくことを考えることに対応します。
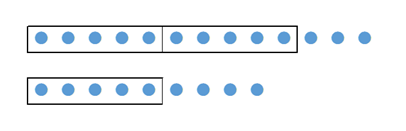
それぞれ、3個、4個余ることがわかります。コードでは、13 % 5 などと計算すれば求められます。
次に、これらの和を $5$ で割った余りを考えます。もちろん足した後に割り算を行って、(13 + 9) % 5 と求めることもできますが、先ほどの図を使えば、別の見方ができると思います。
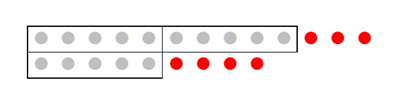
$(13+9)$ 個の丸を5個ずつに分けていくとき、すでに箱に入っていた部分は、もう考える必要はないですよね。それぞれの箱に入らなかった、3個と4個の和に対して余りを求めればOKです。
この例では数が小さすぎてメリットが感じられにくいですが、 $2000000013$ と $2000000009$ との和を $5$ で割ったときの余りならどうでしょうか。両方を足すと、int型の範囲を超えてしまいます。このような、大きな数同士の計算をするには、足す前に余りを計算しておかないと、オーバーフローする可能性があります。
ここで見たように、a, b の和を p で割った余りは、a % p, b % p の和を p で割った余りと等しくなるので、次のように求めることができます。
#include <iostream>
using namespace std;
int main() {
int a = 13, b = 9, p = 5;
cout << (a + b) % p << "\n"; // 2
cout << ((a % p) + (b % p)) % p; // 2
return 0;
}積と余り
今度は、 $13,9$ の積を $5$ で割った余りを考えます。先ほどと同じように、図で考えてみます。
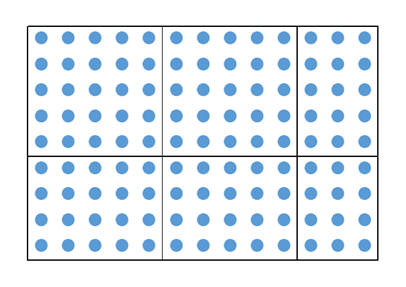
$13, 9$ の積は、上の図の丸の数です。多いですね。また、左上から5個ずつのところに区切りを入れています。
縦か横に5個並んでいる箱に入っている丸の数は、必ず5個ずつに分けることができます。これは $5$ で割り切れるということなので、余りを考える上では無視してもかまいません。つまり、次の図のグレーの部分は、無視していいことになります。

ということで、結局考えるべきなのは、右下の部分だけです。つまり、13, 9 の積を 5 で割った余りは、13 % 5 と 9 % 5 の積を 5 で割った余りと等しくなります。
$13\times 9$ は暗算では少し大変ですが、 $3\times 4$ なら余裕ですし、これを $5$ で割って余りを求めることも楽ですね。
ここで見たように、 a, b の積を p で割った余りは、a % p, b % p の積を p で割った余りと等しくなるので、次のように求めることができます。
#include <iostream>
using namespace std;
int main() {
int a = 13, b = 9, p = 5;
cout << (a * b) % p << "\n"; // 2
cout << ((a % p) * (b % p)) % p; // 2
return 0;
}掛け算の場合は、足し算のときよりも計算結果が大きくなりやすいので、余りを計算する場合は、毎回余りを計算したほうがいいです。例えば、 $2^{100}$ を $10^9+7$ で割った余りを計算するなら、次のようにしたほうがいいでしょう。
#include <iostream>
using namespace std;
int main() {
int a = 1, n = 100, MOD = 1e9 + 7;
for (int i = 0; i < n; i++) {
a = (a * 2) % MOD;
}
cout << a; // 976371285
return 0;
}for文の中で a *= 2 として、最後に cout << a % MOD; とする方法では、掛け算をすべて計算しきる前にオーバーフローしてしまうため、うまく計算できません。一方、2倍するたびに余りを求めると、int型の範囲で計算できるため、うまく答えが出せるようになります。
ここで見た内容を踏まえると、AtCoder ABC 055 B - Training Camp が解けるでしょう。
差と余り
和の余り、積の余りと比べると頻度は少ないですが、差を何かで割ったときの余りを求めることもあります。和や積のときと同じように計算できるのですが、少しだけ注意が必要です。
たとえば、 $13-9$ を $5$ で割った余りを考えましょう。それぞれの余りの差を考えると $3-4=-1$ となってしまいます。負の整数のまま計算すると話がややこしくなるので、次のような手法をよく使います。
#include <iostream>
using namespace std;
int main() {
int a = 13, b = 9, p = 5;
cout << (a - b) % p << "\n"; // 4
cout << (a % p - b % p) % p << "\n"; // -1
cout << (a % p - b % p + p) % p; // 4
return 0;
}余りの差を計算すると負になる可能性があります(上の2つ目の結果)。そのため、p を足して無理やり正にしています。これで、差を割ったときの余りが、0以上の値として求められます。どうして p を足してもいいのかは、次で紹介する考え方を使うとわかりやすいでしょう。
ぐるぐる回って余りを求める
余りの計算を考えるときに使える図をもう一つ紹介します。次のように、円形に $0$ から $4$ までの整数を並べて、 $5$ で割った余りを考えることにしましょう。

$13$ を $5$ で割った余りを考えるには、 $0$ から出発して、時計回りに回転していきます。 $13$ 進むと、 $3$ のところで止まります。これが 13 % 5 = 3 に対応しています。割り算の余りを、「何度も $5$ を引いて残りを求める」と考える(参考:整数の割り算)のではなく、「 $5$ 増えるたびにリセットして残りを求める」と考えているわけです。
この発想で行けば、(13 + 9) % 5 を求めるには、 $13+9$ だけ進めばいいですが、1周すると元の位置に戻ることから、(3 + 4) % 5 と一致することがわかるでしょう。
(13 - 9) % 5 を求めるには、 $13$ だけ進んだ後、今度は反時計回りに $9$ だけ進むときを考えればいいです。1周するたびにリセットされるので、時計回りに $3$ 進み、続いて反時計回りに $4$ 進んだことと同じ結果になります。
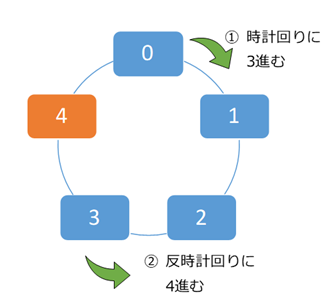
結局、オレンジの部分、つまり、スタートから反時計回りに $1$ 進んだ場所に移動するということです。先ほどの「差と余り」のところで出てきた $-1$ がこの結果に対応しています。図を見てもわかる通り、 $-1$ は $-1+5$ と計算しても同じ場所を指すことがわかります。
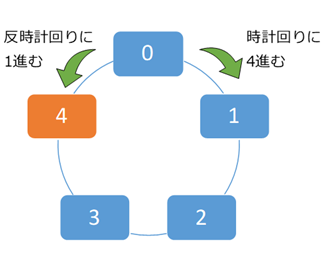
先ほど、差の余りを計算するときに、cout << (a % p - b % p + p) % p; と書きました。余りの差はマイナスになることがあるので、 p を足していますが、なぜ p を足しても同じになるかは、上の図からわかるでしょう。反時計回りに $1$ 進むのと、時計回りに $p-1$ だけ進むことが同じなので、足して正になるように変形していることになります。
この「ぐるぐる回転して余りを求める方法」は、整数同士の和や差の余りを考えるときには使えます。積の余りを考えるには向いてません。
和・差・積の余りの関係を数式で表す
最後に、ここまでに見て内容を、数式で表すことにしましょう。コードを書く上では数式で表す必要はないですが、競プロの問題文や解説文で数式が登場するので、慣れておくことも重要です。
まず、 $p$ を正の整数とします。このとき、 $a, b$ を $p$ で割ったときの余りと、 $m, n$ を $p$ で割ったときの余りがそれぞれ等しいとします。これを数式では次のように表すのでした(参考:整数の割り算)。
\begin{eqnarray}
& & a\equiv m \pmod p \\[5pt]
& & b\equiv n \pmod p \\[5pt]
\end{eqnarray}ここまで見た内容を使えば、\[ a+b \equiv m+n \pmod p \]が成り立つことがわかります。和の余りは、結局余りの和を考えればいいからです。差の場合、積の場合も同じように数式で表すと、
\begin{eqnarray}
& & a-b\equiv m-n \pmod p \\[5pt]
& & ab \equiv mn \pmod p \\[5pt]
\end{eqnarray}となります。
この性質を利用した計算例を挙げましょう。この性質を使えば、 $15^{100}$ を $7$ で割った余りを出すことができます。 $15$ を $7$ で割った余りは $1$ なので、 $15$ を100回掛けて $7$ で割ったときの余りは、 $1$ を100掛けて $7$ で割った余りと同じです。つまり、余りは $1$ です。 $15^{100}$ がどんな数かはわからないし、プログラム上では計算するのは大変ですが、 $7$ で割った余りはすぐに出せるんですね。いつでも簡単な計算になるとは限りませんが、なかなか強力な武器であることはわかるでしょう。
おわりに
ここでは、和・差・積を割った余りの計算について見てきました。余りの計算は他にもありますが、内容が難しいので徐々に見ていくことになります。
数学の内容として学びたい場合は、高校生向けの記事ですが、【基本】整数の和や積と余りやリンク先の下にある関連記事が参考になるでしょう。





