【基本】三角比と測量
ここでは、三角比の表・値を使って、距離や高さを求める問題を見ていきます。事前に【基本】三角比の定義(直角三角形による定義)を見て、三角比の定義をしっかりおさえておきましょう。
三角比の表
大体、高校数学の教科書や参考書には、「三角比の表」が載っています。形式はバラバラですが、通常は、1度ごとに三角比の値が載っています。
三角比の表を使えば、例えば「 $\sin 25^{\circ}$ はどのくらいの値かな」などと思ったときに調べることができます。逆に、「 $\tan$ が $0.7$ になるときの角度はどのくらいかな」と調べることもできます。
実際の試験では、三角比の表がまるまる与えられるケースはあまりありません。載っていても一部分です。三角比の値が与えられるのは、問題文中で「 $\sin 25^{\circ} = 0.4226$ として計算しなさい」などと指定されるケースが多いです。
例題
次のような問題を考えてみましょう。
$\sin 25^{\circ} = 0.4226$, $\cos 25^{\circ} = 0.9063$, $\tan 25^{\circ} = 0.4663$
問題文中にある、仰角(ぎょうかく、elevation angle)は見上げた視線と水平面とのなす角のことを言います。「仰」は「天を仰(あお)ぐ」というように、上を見る時に使います。逆に、見下ろした視線と水平面とのなす角は俯角(ふかく、depression angle)といいます。高い場所から見下ろすことを「俯瞰(ふかん)する」といいますが、その「俯」が使われています。
さて、今の状況を図にすると、次のようになります。
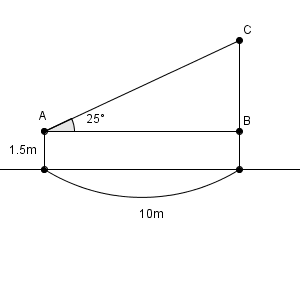
左に人がいて、右に木がある、という図です。仰角が25度であることと 10m 離れていることが分かっていて、高さが分からない、という状況です。
このとき、三角比の中で使えるものは、 $\tan$ ですね。 $\tan\angle\mathrm{ CAB }=\dfrac{\mathrm{ BC } }{\mathrm{ AB } }$ であり、AB がすでにわかっていて BC が求められればいいからです。定義を思い出せば正しく選べるはずです。
これをもとにすれば、次のように求めることができます。
\begin{eqnarray}
& & 1.5 + \mathrm{ BC } \\
&=& 1.5 + \mathrm{ AB } \times \tan \angle \mathrm{ CAB } \\
&=& 1.5 + 10 \times \tan 25^{\circ} \\
&=& 1.5 + 10 \times 0.4663 \\
&=& 6.163 \\
\end{eqnarray}このことから、答えは 6.2m となります。
おわりに
ここでは三角比を使って、木の高さを求める問題を考えてみました。図をかいて、三角比の定義を使えば解けましたね。定義さえちゃんとわかっていれば、すぐに解けるでしょう。





