【基本】三角比の定義（直角三角形による定義）

🕒 2016/09/17 🔄 2023/05/01

ここでは、三角比の定義を見ていきます。今後、三角比の勉強をしていくうえでの基本事項です。

📘 目次

角度と辺の比

直角三角形は、どちらかの鋭角の大きさを決めると、三角形の形が決まります。

例えば、 $\triangle \mathrm{ABC}$ と $\triangle \mathrm{DEF}$ があったとします。 $\angle \mathrm{C} = \angle \mathrm{F} = 90^{\circ}$ の直角三角形で、 $\angle \mathrm{B} = \angle \mathrm{E}$ だったとしましょう。このとき、この2つの三角形は相似になります。

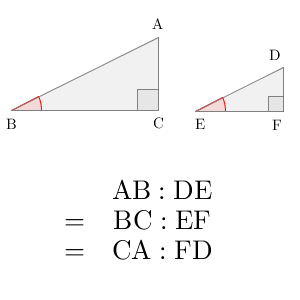
相似な図形は辺の比が等しいので、 \[ \mathrm{AB}:\mathrm{DE} = \mathrm{BC}:\mathrm{EF} = \mathrm{CA}:\mathrm{FD} \]が成り立ちます。このことから、「角度に辺の比を対応させる」という発想が生まれてきます。

sin・cos・tanの定義

直角三角形の場合、どちらかの鋭角の大きさを決めると、三角形の形が決まり、辺の比も決まります。このことを利用して、角度に辺の比を対応させることを考えていきます。次の3つの「辺の比」を考えます。

1つ目は、 $\sin$ (sine、サイン)です。日本語では正弦といいます。次の図で言う、「斜辺分の縦」です。

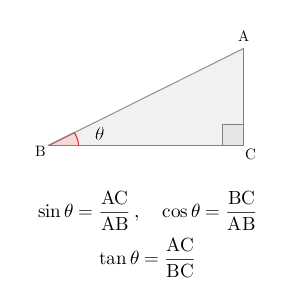
$\theta$ という角度に対してのサインである、という意味で、次のように書きます。\[ \sin \theta = \frac{\mathrm{AC} }{\mathrm{ AB } } \]「sin」でひとかたまりの記号です。「sかけるiかけるn」という意味ではありません。なお、 $\theta$ は「シータ」と読みます。角度を表すときによく使われるギリシャ文字です（参考：ギリシャ文字一覧）。

2つ目は、 $\cos$ (cosine、コサイン)です。日本語では余弦といいます。上の図で言う「斜辺分の横」で、式で書くと次のようになります。\[ \cos \theta = \frac{\mathrm{BC} }{\mathrm{ AB } } \]

最後に、 $\tan$ (tangent、タンジェント)です。日本語では正接といいます。上の図で言う「横分の縦」です。式で書くとこうなります。\[ \tan \theta = \frac{\mathrm{AC} }{\mathrm{ BC } } \]

この3つを合わせて、三角比と呼びます。実は他にもあるのですが、高校数学ではこの3つだけしか出てきません。

当面は、鋭角（0度より大きく、90度より小さい角）のみを考えます。

今の段階では、「こんなものを考えてどうなるんだろう？」という気がすると思いますが、三角比の分野を学ぶと、いろんな辺の長さや角の大きさを求められるようになり、便利さがわかってきます。

$\theta = 30^{\circ}, 45^{\circ}, 60^{\circ}$ のとき、三角比の値はどうなるでしょうか。上の図を見ながら辺の比を考えればわかりますね。例えば、 $\displaystyle \sin 30^{\circ} = \frac{1}{2}$, $\displaystyle \cos 45^{\circ} = \frac{\sqrt{2} }{2}$, $\tan 60^{\circ} = \sqrt{3}$ などとなります。