【基本】余角の三角比
ここでは、余角の三角比、つまり、 $90^{\circ}-\theta$ の三角比について見ていきます。
余角
直角三角形の1つの鋭角が $\theta$ の場合、残りの鋭角は $90^{\circ}-\theta$ になりますね。
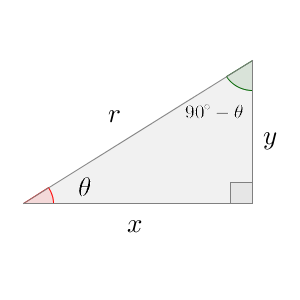
$\angle \mathrm{ A }+\angle \mathrm{ B }=90^{\circ}$ のとき、 $\angle \mathrm{ B }$ は $\angle \mathrm{ A }$ の余角(よかく、complementary angle)といいます。
次で見るように、余角の三角比は、元の角の三角比と関係があります。
余角の三角比
元の角の三角比とその余角の三角比とを比べてみます。それぞれ、左下に対象の角度が来るように、図をかいてみます。
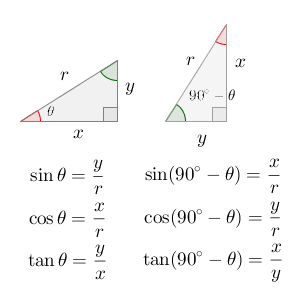
図の右側を見ながら、 $90^{\circ}-\theta$ の三角比を見てみましょう。
まずは、 $\sin ( 90^{\circ}-\theta )$ です。 $\sin$ の定義通り考えると、\[ \sin(90^{\circ}-\theta)=\frac{x}{r} \]となります。この式は、元の角度の $\cos$ ですね。なので、次の式が成り立ちます。\[ \sin(90^{\circ}-\theta) = \cos\theta \]もう一度同じ図を見てみましょう。

2つの直角三角形を比べたとき、縦と横が入れ替わっていることに注目すれば、 $\sin(90^{\circ}-\theta) = \cos\theta$ となることは理解しやすいと思います。同じように考えると、 $\cos$ には次のような関係式が成り立つことが分かります。\[ \cos(90^{\circ}-\theta) = \sin\theta \]
最後に、 $\tan$ です。図から考えると、次のようになります。\[ \tan(90^{\circ}-\theta)=\frac{x}{y} \]となります。この式は、元の角度の $\tan$ の逆数ですね。なので、次の式が成り立ちます。\[ \tan(90^{\circ}-\theta) = \frac{1}{\tan\theta} \]
以上をまとめると、余角の三角比は次のようになります。
- $\sin(90^{\circ}-\theta) = \cos\theta$
- $\cos(90^{\circ}-\theta) = \sin\theta$
- $\displaystyle \tan(90^{\circ}-\theta) = \frac{1}{\tan\theta}$
例題
余角の三角比を用いた問題を解いてみましょう。
(1) $\displaystyle \sin\frac{A}{2} = \cos\frac{B+C}{2}$
(2) $\displaystyle \tan\frac{A}{2} \tan\frac{B+C}{2} = 1$
少し難しいですね。分母に2があることに注目しましょう。 $A+B+C=180^{\circ}$ であることに注意すると、\[ \frac{B+C}{2}=\frac{180^{\circ}-A}{2}=90^{\circ}-\frac{A}{2} \]となります。つまり、余角の三角比が使えるということですね。
(1)は次のようになります。右辺を変形していきます。
\begin{eqnarray}
\cos\frac{B+C}{2}
&=&
\cos\left(90^{\circ}-\frac{A}{2}\right)\\
&=&
\sin \frac{A}{2}\\
\end{eqnarray}となり、左辺と一致します。
(2)は左辺を変形していきます。
\begin{eqnarray}
\tan\frac{A}{2}\tan\frac{B+C}{2}
&=&
\tan\frac{A}{2}\tan\left(90^{\circ}-\frac{A}{2}\right)\\
&=&
\tan\frac{A}{2} \times \frac{1}{\tan\frac{A}{2} }\\
&=&
1
\end{eqnarray}となり、右辺と一致します。
おわりに
ここでは、余角の三角比について見てきました。直角三角形をかいて見比べれば、関係式は理解できると思います。実際の問題で使うときには、「 $90^{\circ}-\theta$ 」の形を見て、ピンと来ないといけません。





