【基本】三角比の相互関係

🕒 2016/09/19 🔄 2023/05/01

【基本】三角比の定義（直角三角形による定義）で、$\sin$, $\cos$, $\tan$ の3つの三角比を紹介しました。これらは互いに独立した値ではなく、ある関係式を満たします。ここでは、その相互関係について見ていきます。

📘 目次

三角比の相互関係

直角三角形と三角比の対応は下の図の通りでしたね。

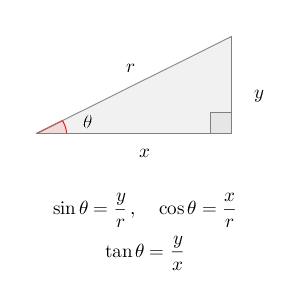
これから、 $y=r\sin\theta$ と $x=r\cos\theta$ という式が得られます。ちなみに、 $y=\sin\theta r$ とは書きません。「 $(\sin\theta)\times r$ 」なのか「 $\sin(\theta\times r)$ 」なのかがわからないからです。

さて、この2つの式を、 $\tan$ の式に入れて見ましょう。
\begin{eqnarray} \tan \theta &=& \frac{y}{x} \\[5pt] &=& \frac{r\sin\theta}{r\cos\theta} \\[5pt] &=& \frac{\sin\theta}{\cos\theta} \\[5pt] \end{eqnarray}このようになります。これは、辺の長さが出てこない、三角比だけの関係式です。

また、直角三角形なので、三平方の定理（ピタゴラスの定理）が成り立ちます。 $x^2+y^2=r^2$ です。これに三角比の式を代入してみます。
\begin{eqnarray} (r\cos\theta)^2 +(r\sin\theta)^2 &=& r^2 \\ (\sin\theta)^2 +(\cos\theta)^2 &=& 1 \\ \end{eqnarray}三角比の場合、 $(\sin\theta)^2$ のことを $\sin^2\theta$ と書きます。なので、この式は\[ \sin^2\theta + \cos^2\theta=1 \]となります。これも三角比だけの関係式です。

最後に、2つ目で得られた式の両辺を、 $\cos^2\theta$ で割ってみます。1つ目で得られた式も使うと、次のような式が得られます。
\begin{eqnarray} \frac{\sin^2\theta}{\cos^2\theta} +1 &=& \frac{1}{\cos^2\theta} \\[5pt] \tan^2\theta +1 &=& \frac{1}{\cos^2\theta} \\ \end{eqnarray}これも三角比だけの関係式ですね。

ここで紹介した3つの式が、基本的な三角比の相互関係です。三角比だけからなる関係式です。まとめておきます。

三角比の相互関係

$\theta$ が鋭角のとき、次が成り立つ。

$\displaystyle \tan\theta = \frac{\sin\theta}{\cos\theta}$
$\sin^2\theta +\cos^2\theta = 1$
$\displaystyle \tan^2\theta +1 = \frac{1}{\cos^2\theta}$

これがあれば、「3つある三角比のどれか1つの値がわかると、残りの2つの値もわかる」というメリットがあります。例題で確かめてみましょう。

例題

三角比の相互関係を使った例題を解いてみましょう。

例題

$\theta$ は鋭角とする。
(1) $\displaystyle \cos\theta=\frac{1}{3}$ のとき、 $\sin\theta$ と $\tan\theta$ の値を求めなさい。
(2) $\tan\theta=2$ のとき、 $\sin\theta$ と $\cos\theta$ の値を求めなさい。

「 $\theta$ は鋭角とする」という条件は、現時点ではあまり深く考えなくてもいいです。「三角比は直角三角形の辺の比で定義しているから、三角比の値は正になる」ということだと解釈しておきましょう。

(1)は、まず、相互関係の2つ目の式を使って $\sin$ を求めましょう。
\begin{eqnarray} \sin^2\theta &=& 1-\cos^2\theta = \frac{8}{9} \\ \sin\theta &=& \frac{2\sqrt{2} }{3} \\ \end{eqnarray}この結果と、相互関係の1つ目の式を使います。 \begin{eqnarray} \tan\theta &=& \frac{\sin\theta}{\cos\theta} \\ &=& \frac{2\sqrt{2} }{3} \div \frac{1}{3} \\ &=& 2\sqrt{2} \\ \end{eqnarray}となります。

(2)は、相互関係の3つ目の式を使って、まず $\cos$ を求めます。 $\tan$ と $\sin$ だけの関係式がないので、これを使うしかないですね。
\begin{eqnarray} \tan^2\theta +1 &=& \frac{1}{\cos^2\theta} \\ 2^2 +1 &=& \frac{1}{\cos^2\theta} \\ \cos^2\theta &=& \frac{1}{5}\\ \cos\theta &=& \frac{\sqrt{5} }{5}\\ \end{eqnarray}これと、相互関係の1つ目の式から \begin{eqnarray} \sin\theta = (\tan\theta) \times (\cos\theta)=\frac{2\sqrt{5} }{5} \end{eqnarray}が得られます。

なお、ここでは、説明上、「相互関係の〇つ目から～」と書いていますが、別に順番が決まっているわけではありません。試験では、「相互関係から～」と書くだけで大丈夫です。