【基本】無理関数のグラフ(放物線の一部)
ここでは、無理関数 $y=\sqrt{ax+b}$ のグラフについて見ていきます。
無理関数のグラフ
【基本】無理関数では、無理関数 $y=\sqrt{ax}$ のグラフについて見ましたが、ここでは、 $y=\sqrt{ax+b}$ の場合にはどうなるかを考えていきます。
$y=\sqrt{2x+3}$ のグラフがどうなるかを考えてみましょう。無理関数の場合は、定義域に注意が必要なのでした。根号の中が0以上の部分だけが定義域なので、\[ x\geqq -\dfrac{3}{2} \]が定義域となります。
この範囲で、具体的な値を代入して、わかりやすい点をいくつかピックアップしてみましょう。 $x=-\dfrac{3}{2},0,3$ と代入すると $y=0,\sqrt{3},3$ となります。
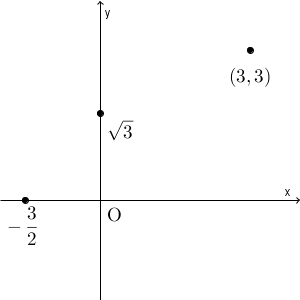
これらを滑らかにつなげていくと、次のようになります。
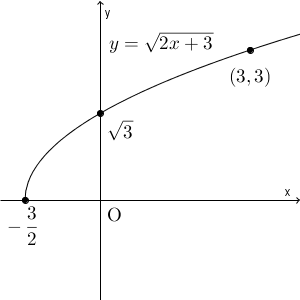
元の式を2乗すると、 $y^2=2x+3$ となります。 $x,y$ を入れ替えれば $x^2=2y+3$ となり、変形すれば\[
y=\frac{1}{2}x^2-\frac{3}{2} \]となります。つまり、放物線ですね。 $x,y$ を入れ替えるということは、縦と横を入れ替えるということなので、滑らかにつないだものがグラフとなる、と考えて構いません。
ちなみに、縦と横を入れ替えたものも合わせてかくと、こうなります。
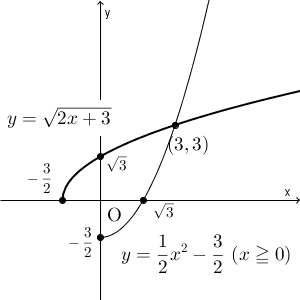
一般に、 $y=\sqrt{ax+b}$ のグラフは、放物線の一部になります。
無理関数のグラフと平行移動
先ほど $y=\sqrt{2x+3}$ のグラフを見ましたが、これと式の形が似ている $y=\sqrt{2x}$ のグラフとはどのような関係があるでしょうか。両者を並べてみましょう。
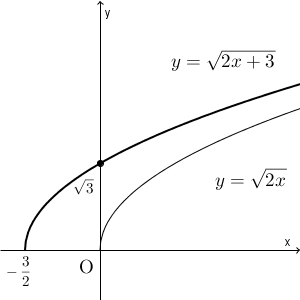
$y=\sqrt{2x+3}$ で、 $x=0,1,2$ としたときと $y$ 座標が同じになるのは、 $y=\sqrt{2x}$ でいうと、 $x=\dfrac{3}{2},\dfrac{5}{2},\dfrac{7}{2}$ となります。つまり、 $y=\sqrt{2x+3}$ のグラフは、 $y=\sqrt{2x}$ のグラフを $x$ 軸方向に $-\dfrac{3}{2}$ だけ移動したものになる、と予想できます。

この予想を、式で計算して確認してみましょう。 $y=\sqrt{2x}$ 上の点 $(X,Y)$ を、 $x$ 軸方向に $-\dfrac{3}{2}$ だけ平行移動したら $(x,y)$ に移るとします。つまり、\[ X-\dfrac{3}{2}=x,\ Y=y \]ということです。 $X,Y$ は\[ Y=\sqrt{2X} \]を満たすので、ここに、 $x,y$ を代入すれば\[ y=\sqrt{2\left(x+\dfrac{3}{2}\right)}=\sqrt{2x+3} \]となります。移動した後の点が、 $y=\sqrt{2x+3}$ を満たすことがわかります。よって、たしかに、 $y=\sqrt{2x+3}$ のグラフは、 $y=\sqrt{2x}$ のグラフを $x$ 軸方向に $-\dfrac{3}{2}$ だけ移動したものになることがわかります。
一般に、 $y=\sqrt{a(x-p)}+q$ のグラフは、 $y=\sqrt{ax}$ のグラフを $x$ 軸方向に $p$, $y$ 軸方向に $q$ だけ平行移動したもの、となります。
無理関数のグラフの例
今まで見てきたことを踏まえて、無理関数のグラフの例をいくつかみておきましょう。
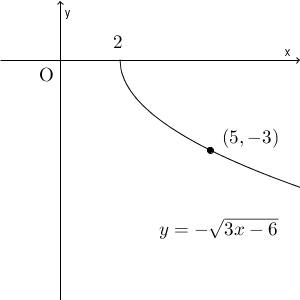
$y=-\sqrt{3x-6}$ のグラフを考えましょう。これは、 $y=\sqrt{3x}$ のグラフを平行移動した、と考えて次のように変形します。
\begin{eqnarray}
y
&=&
-\sqrt{3x-6} \\[5pt]
&=&
-\sqrt{3(x-2)} \\[5pt]
\end{eqnarray}これより、 $y=-\sqrt{3x}$ のグラフを $x$ 軸方向に $2$ だけ平行移動すればいいことがわかります。グラフは次のようになります。
$y=\sqrt{-2x-1}+3$ のグラフはどうなるでしょうか。これも今までと同じように変形します。
\begin{eqnarray}
y
&=&
\sqrt{-2x-1}+3 \\[5pt]
&=&
\sqrt{-2\left(x+\dfrac{1}{2}\right)}+3 \\[5pt]
\end{eqnarray}となります。これより、 $y=\sqrt{-2x}$ のグラフを、 $x$ 軸方向に $-\dfrac{1}{2}$, $y$ 軸方向に $3$ だけ平行移動したグラフになることがわかります。
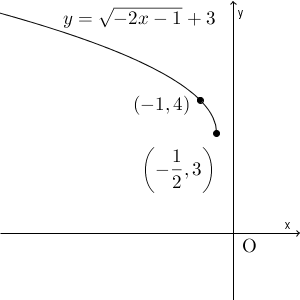
グラフは次のようになります。変なところから突然始まるようなグラフになっていますが、これであっています。
実際にグラフをかくときには、根号の中が $0$ となる場合を考え、そこからどっち向きにグラフが伸びていくかを考えると間違いにくいです。 $x$ の前にマイナスがなければ右へ、あれば左へ伸びます。根号の前にマイナスがなければ上へ、あれば下へ伸びます。具体的な値を入れれば、すぐに確かめられます。
おわりに
ここでは、無理関数 $y=\sqrt{ax+b}$ のグラフを見てきました。 $y=\sqrt{ax}$ をどのように平行移動したグラフかがわかるようになっておきましょう。





