【基本】無理関数
ここでは、無理関数について見ていきます。
無理関数
【基本】一次分数関数でも見たように、今後の学習をしていく上で知っておきたい関数がいくつかあります。無理関数もそのような関数の1つです。
$\sqrt{x}$ や $\sqrt{2x+3}$ というように、根号の中に文字を含む式を、無理式と言います。この無理数で表された関数を、無理関数といいます。
$y=\sqrt{x}$ や $\sqrt{2x+3}$ は無理関数です。また、 $y=\sqrt{x^2+x+1}$ や $y=\sqrt{-\dfrac{x}{x+1} }$ や $y=\sqrt[3]{x}$ なども無理関数です。
無理関数の定義域と値域
分数関数では、分母が $0$ になる値を定義域から外す必要がありました。無理関数でも、定義域について制限があります。
通常、何も断りがなければ、定義域は、根号の中が0以上となる実数全体、となります。根号の中が負だと、実数にならないからですね。 $y=\sqrt{x}$ の場合であれば、定義域は $x\geqq 0$ となります。 $y=\sqrt{2-x}$ であれば、定義域は $x\leqq 2$ となります。 $y=\sqrt{x^2+1}$ であれば、根号の中はつねに正なので、定義域は実数全体となります。
また、 $\sqrt{ax}$ の値は0以上なので、値域も0以上となります。 $\sqrt{\quad}$ の部分は0以上だからです。
無理関数は、定義域も値域も制限されることに注意しましょう。
最もシンプルな無理関数のグラフ
$y=\sqrt{x}$ という無理関数のグラフを考えてみましょう。
定義域は $x\geqq 0$ ですね。 $x=0,1,2,3,4$ と代入してみると、そのままですが、 $y=0,1,\sqrt{2},\sqrt{3},2$ となります。これをもとに点をとると、次のようになります。
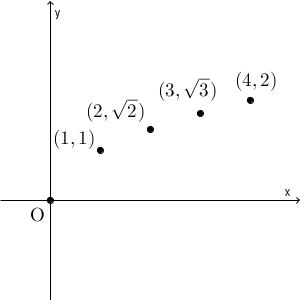
これをもとに滑らかにつなぐと、次のようになります。
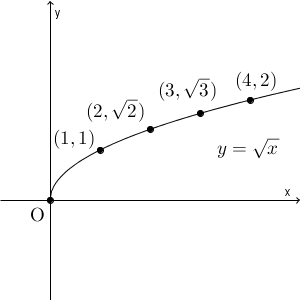
滑らかにつないでしまってもいいのか、と思うかもしれないですが、これはすでに知っている関数の応用なんですね。両辺を2乗してみると\[ y^2=x \]となります。ここで、 $x$ と $y$ を入れ替えると、\[ y=x^2 \]となります。つまり、放物線なんですね。 $y=\sqrt{x}$ のグラフは、放物線の一部、となります。
放物線全体とはならないことに注意しましょう。先ほども見た通り、値域は0以上なので、上半分だけになります。では、下半分となるのはどういうときかというと、根号の前にマイナスがついたとき、つまり、 $y=-\sqrt{x}$ のときとなります。
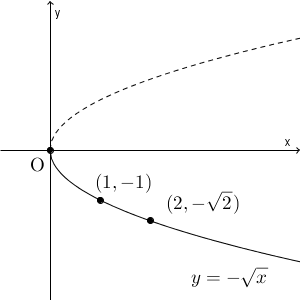
上は、$y=-\sqrt{x}$ のグラフです。
次に、$y=\sqrt{-x}$ のグラフならどうなるかも見ておきましょう。
今度は、定義域は0以下です。 $x=0,-1,-2,-3,-4$ と代入していき、同じように点をつなげてグラフをかいてみましょう。放物線の一部になることがわかっているので、点をなめらかにつなげればOKです。
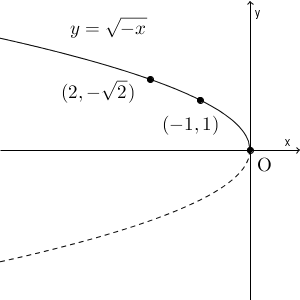
最後に、 $y=-\sqrt{-x}$ のグラフです。
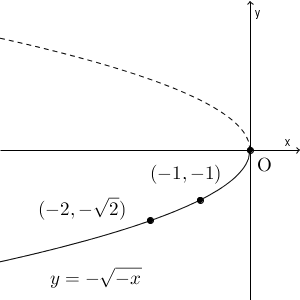
実際にグラフを見ると、無理関数は定義域や値域が制限される、ということがわかります。 $\sqrt{\quad}$の中が0以上、それ自体も0以上、という点に注意しましょう。
おわりに
ここでは、無理関数の紹介、そして、シンプルなケースでグラフがどうなるかを見ました。定義域、値域に気を付けるようにしましょう。





