【基本】順列

ここでは、「1列に並べる方法が何通りあるか」という問題を見ていきます。場合の数の分野では、とても基本的な問題です。

4つのものを1列に並べる方法

「A, B, C, D の4つの文字を1列に並べる方法が何通りあるか」を考えてみましょう。この問題は【基本】まとめて数えるでも出てきました。樹形図をかくと、次のように同じ構造をしている部分が見つかるんでしたね。

さらに、赤い箱の中にも、同じ構造をしている部分があります。

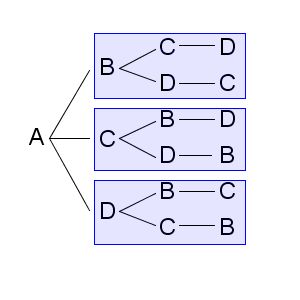
赤い箱が4つあり、各赤い箱について、同じ構造をした青い箱が3つあります。また、それぞれの青い箱の中に2通りの並べ方があるので、\[ 4\times 3\times 2=24 \]通りと求められます。

この「同じ構造をまとめて、掛け算で求める」というのは、【基本】樹形図と積の法則でみた「積の法則」の考え方を使っています。

6人から3人を選んで1列に並べる方法

今度は、全員を並べるのではなく、一部の人だけを並べる方法を考えてみます。また、今回は、上の樹形図での考え方を踏まえつつ、樹形図をかかずに求めてみたいと思います。

もし、樹形図をかくなら、1番目の並び方で枝分かれしますね。枝の数はもちろん6本です。

続いて、2番目に並ぶ人は、1番目以外の5人のうちの誰かで枝分かれします。枝の数は、5本です。

そして、3番目に並ぶ人は、1番目と2番目を除いた4人のうちの誰かで枝分かれします。枝の数は4本ですね。

1番目を決めた後の樹形図の形は、条件が同じだから、どれも構造は同じです（もちろん、誰が並んでいるかは違いますが）。2番目を決めた後の樹形図の形も、それぞれ同じです。なので、まとめて計算することができて、\[ 6\times 5\times 4=120 \]通りとなります。

樹形図内の同じ構造になる部分をまとめると、掛け算を使って並べ方の総数を求めることができます。

順列

上で見たように、いくつかのものに順序をつけて1列に並べる配列を順列(permutation)といいます。また、「異なる n 個のものから r 個を取り出して、1列に並べる方法」（ただし $r\leqq n$ とする）の総数は、 ${}_n \mathrm{ P }_r$ で表します。 P の左下に全体の数、右下に並べる数を書きます。よく出てくるので、こういう記号が用意されています。

例えば、先ほどの「6人から3人を選んで1列に並べる方法」の総数は、 ${}_6 \mathrm{ P }_3$ と書きます。

${}_n \mathrm{ P }_r$ はもう少し具体的な式で書くことができます。「6人から3人を選んで1列に並べる方法」のときと同じように考えると、

　1番目を並べる方法は $n$ 通り
　2番目を並べる方法は $n-1$ 通り
　3番目を並べる方法は $n-2$ 通り
　　$\vdots$
　r 番目を並べる方法は $n-r+1$ 通り

となるため、これらを掛け合わせたものが総数になります。つまり、次が成り立ちます。

上の例題の結果を、 P を用いて表すと\[ {}_6 \mathrm{ P }_3 = 6\times 5\times 4=120 \]となります。

階乗

上では「6人から3人を選んで1列に並べる」ケースを見ましたが、続いて1つ目のケース「4個のものを1列に並べる」ケースについて考えてみましょう。これを P を使って表すと\[ {}_4 \mathrm{ P }_4 = 4\times 3\times 2 \times 1=24 \]となります。「4個から4個を選んで1列に並べる」と考えるわけですね。

このように、「異なる n 個のものをすべて並べる順列の総数」は、 $1$ から n までの整数をすべて掛け合わせた数になります。これもよく使うので、 $n!$ という記号で表します。これを「 n の階乗(factorial)」といいます。

式でまとめると、次のようになります。

おわりに

ここでは、順列について見てきました。また、順列でよく使う記号 ${}_n \mathrm{ P }_r$ と $n!$ についても見てきました。

今後、「1列に並べる方法」を数えるときには、突然これらの記号が出てくることになります。しかし、背景には樹形図での書き出しがあることを忘れないようにしておきましょう。