【基本】ベクトルの平行
ここでは、「ベクトルが平行である」とはどういうことを言うのか、について見ていきます。
ベクトルの平行
【基本】ベクトルの定数倍で見たように、 $\overrightarrow{ \mathrm{ AB } }(\ne\vec{0})$ に定数 k$(\ne 0)$ を掛けたベクトル $k\overrightarrow{ \mathrm{ AB } }$ は、 $\overrightarrow{ \mathrm{ AB } }$ と向きが同じか反対になります。
なので、仮に $\overrightarrow{ \mathrm{ CD } }=k\overrightarrow{ \mathrm{ AB } }$ を満たすベクトル $\overrightarrow{ \mathrm{ CD } }$ があったとすると、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ CD } }$ の向きは、同じか反対です。そのため、どちらにしろ、 AB と CD は平行になります。
このことから、2つのベクトルの向きが同じか反対のとき、「2つのベクトルは平行である」と言います。直線のときと同じように、\[ \overrightarrow{ \mathrm{ AB } } /\!/ \overrightarrow{ \mathrm{ CD } } \]と書きます。
また、 AB と CD が平行なら、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ CD } }$ は向きが同じか反対なので、長さを調整するように定数を掛ければ等しくなるようにできます。
以上から、「ベクトルの平行」について、次のことが言えます。
$\vec{a} /\!/ \vec{b}$ $\iff$ $\vec{b}=k\vec{a}$ となる実数 k が存在する
「ベクトルを k 倍したものと、元のベクトルとは、平行になる」と考えれば、そんなに新鮮さは感じられないかもしれません。しかし、ここで重要なのは、「2つの線分が平行であることをベクトルを使って示すには、ベクトルが定数倍になることを示せばいい」、この言い換えができることなんですね。以下ではこのことについて見ていきます。
ベクトルと中点連結定理
中学のときに習う中点連結定理を、ベクトルの世界で考えてみましょう。
三角形 ABC があって、辺 AB, AC の中点を、それぞれ M, N とおきます。このとき、 MN は BC と平行で、長さが $\dfrac{1}{2}$ になる、というのが、中点連結定理の内容です。
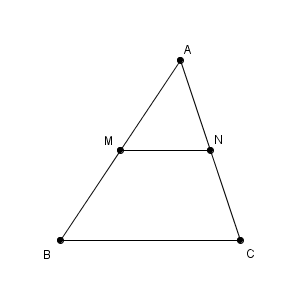
中学の範囲では、相似を使って示しますが、ここでは、ベクトルで考えてみましょう。
M, N は辺 AB, AC の中点であることから、 $\overrightarrow{ \mathrm{ AM } }=\dfrac{1}{2}\overrightarrow{ \mathrm{ AB } }$, $\overrightarrow{ \mathrm{ AN } }=\dfrac{1}{2}\overrightarrow{ \mathrm{ AC } }$ となります。
よって、
\begin{eqnarray}
\overrightarrow{ \mathrm{ MN } }
&=&
-\overrightarrow{ \mathrm{ AM } }+\overrightarrow{ \mathrm{ AN } } \\[5pt]
&=&
-\frac{1}{2}\overrightarrow{ \mathrm{ AB } }+\frac{1}{2}\overrightarrow{ \mathrm{ AC } } \\[5pt]
&=&
\frac{1}{2}(-\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ AC } }) \\[5pt]
&=&
\frac{1}{2}\overrightarrow{ \mathrm{ BC } } \\[5pt]
\end{eqnarray}となります。定数倍で書けているので、上で見た内容が使えますね。このことから、 MN は BC と平行であることがわかります。また、 $\dfrac{1}{2}$ 倍しているのだから、長さが半分になることもわかります。
平行であることを示したい2つのベクトルについて、定数倍になることを示しています。
上で示した内容は、中学のときに使った「相似」の要素がまったくないようにも見えますが、ベクトルの和の定数倍に関する部分(上の式の $\dfrac{1}{2}$ でくくったところ)で相似の概念を使っています。【基本】ベクトルの和の定数倍で相似を使っていましたね。つまり、上の証明ではベクトルしか使っていませんが、その裏で相似の性質も使っているんですね。見かけが違うだけで、やっていることは本質的にはほとんど変わりません。
おわりに
ここでは、ベクトルの平行について見てきました。線分が平行であることをベクトルを使って示すなら、定数倍になることを示せばいい、と言い換えられることが重要です。





