【基本】二次関数の最大・最小（定義域に制限あり）

【基本】二次関数の最大・最小では、定義域が実数全体の範囲で、二次関数の最大・最小を考えました。ここでは、定義域に制限がある場合の、最大・最小を考えていきます。

例題

二次関数自体はどれも同じで、定義域の範囲だけが違っています。定義域が実数全体の時と同じように、この場合もグラフをかくのが基本です。

まずは、放物線 $y=x^2+8x+5$ のグラフをかくために、頂点の座標を求めます。
\begin{eqnarray} y &=& x^2+8x+5 \\ &=& (x+4)^2-16+5 \\ &=& (x+4)^2-11 \\ \end{eqnarray}このことから、頂点の座標が $(-4,-11)$ であることが分かるので、グラフをかくと次のようになります。

これを踏まえて、各問題を考えていきます。

(1)は定義域が $-6\lt x \leqq -1$ です。 $y=x^2+8x+5$ の式に代入すると、 $x=-6$ のとき $y=-7$ 、 $x=-1$ のとき $y=-2$ であることがわかるので、このときのグラフは次の実線部分になります。

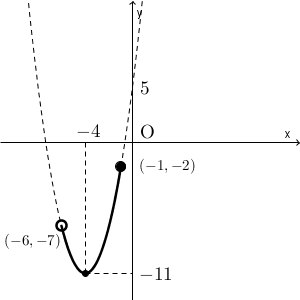
区間の左端は入らないので白丸、右端は入るので黒丸です。

さて、この二次関数の最大値と最小値をグラフから読み取ります。この範囲の中で、 y 座標の一番大きいところと小さいところ（一番高いところと低いところ）が答えになります。最大値となるのは、右端であることが分かりますね。一方、最小値は、頂点の部分になることがわかります。区間の左端ではありません。ここが、一次関数のときと違う点です。

以上から、(1)の答えは、「 $x=-1$ のとき最大値 $y=-2$ をとり、 $x=-4$ のとき最小値 $y=-11$ をとる」となります。

他も同様に、グラフをかいてから考えます。

(2)は、定義域が $-7\lt x \leqq -5$ です。 $y=x^2+8x+5$ の式に代入すると、 $x=-7$ のとき $y=-2$ 、 $x=-5$ のとき $y=-10$ であることがわかるので、このときのグラフは次の実線部分になります。

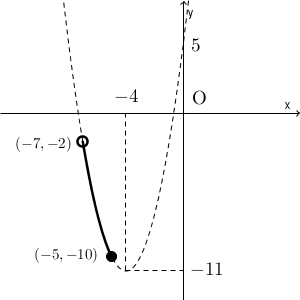
最小値は、区間の右端であることがわかります。(1)では最小値をとるのは頂点のときでしたが、今は頂点が定義域に入っていません。このように、区間がかわることによって、どこで最小値をとるかは変わってきます。

最大値は、区間の左端でとる、と思ってしまいがちですが違います。 $x=-7$ は定義域に含まれないので、 $y=-2$ となることはありません。この場合、「最大値はない」となります。

以上から、(2)の答えは、「 $x=-5$ のとき最小値 $y=-10$ をとる。最大値はない。」となります。

(3)も同じようにグラフをかきます。

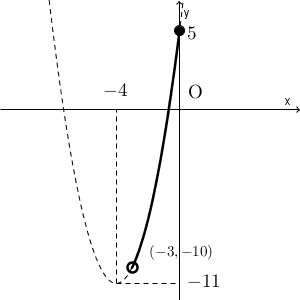
これから、(3)の答えは、「 $x=0$ のとき最大値 $y=5$ をとる。最小値はない。」となります。

おわりに

定義域に制限がある場合の二次関数の最大・最小について見てきました。定義域によって、最大値・最小値をとるところが変わってくるところがポイントでした。例題では下に凸の場合を考えましたが、上に凸の場合も考え方は同じです。グラフを描いて、答えるようにしましょう。

なお、最大値・最小値をとる候補は、区間の両端と頂点です。頂点も候補になることに注意して考えるようにしましょう。