【基本】対数関数の性質

🕒 2018/07/05 🔄 2023/05/01

ここでは、対数関数の大小関係に関する性質を見ていきます。

📘 目次

対数関数のグラフの復習

対数関数 $y=\log_a x$ のグラフの復習をしておきましょう（参考：【基本】対数関数のグラフ）。

対数関数のグラフは、底が $1$ より大きいときと小さいときとで大きく異なるのでした。まず、 $a\gt 1$ のときは、次のように、右肩上がりのグラフになります。 $x=\dfrac{1}{a},1,a$ といった、具体的にいくつか点をとってみると、右肩上がりになることはわかると思います。

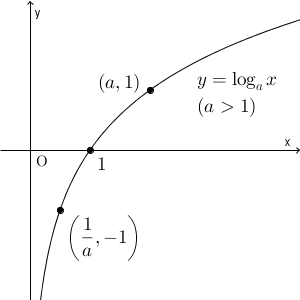
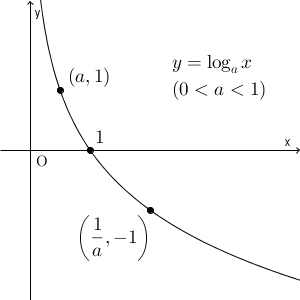
$0\lt a\lt 1$ のときは、逆に、右肩下がりのグラフになります。 $x=a,1,\dfrac{1}{a}$ などの場合を考えればわかるでしょう。 $a\lt 1 \lt \dfrac{1}{a}$ となることに注意しましょう。

どちらの場合も、定義域は正の実数全体、値域は実数全体になります。また、 $y$ 軸が漸近線となります。指数関数のグラフ $y=a^x$ と比べたときに、対数関数のグラフと指数関数のグラフは直線 $y=x$ について対称になることも、【基本】対数関数のグラフで確認しました。

これらをまとめると、次のようになります。

対数関数の性質

$y=\log_a x$ について、次が成り立つ。
$a\gt 1$ のとき
　$0\lt p\lt q$ $\iff$ $\log_a p \lt \log_a q$
$0\lt a \lt 1$ のとき
　$0\lt p\lt q$ $\iff$ $\log_a p \gt \log_a q$

対数関数の大小関係

対数関数のグラフを踏まえて、対数関数の大小関係について考えてみましょう。

例題

小さい方から順番に並び替えなさい。
(1) $\log_2 3$, $\log_4 5$, $\log_8 9$
(2) $\log_{0.5} 3$, $\log_{0.25} 3$, $-1$

(1)を考えましょう。底も真数もどちらも違っていて考えづらいです。しかし、底の変換公式を用いれば、底をそろえることはできます。 $2$ に揃えてみると、
\begin{eqnarray} \log_4 5 &=& \frac{\log_2 5}{\log_2 4} \\[5pt] &=& \frac{1}{2}\log_2 5 \\[5pt] &=& \log_2 \sqrt{5} \\[5pt] \end{eqnarray}となり、 \begin{eqnarray} \log_8 9 &=& \frac{\log_2 9}{\log_2 8} \\[5pt] &=& \frac{1}{3}\log_2 9 \\[5pt] &=& \log_2 \sqrt[3]{9} \\[5pt] \end{eqnarray}となります。

これで底が同じになったので、違うところは真数だけとなりました。真数は、 $3,\sqrt{5},\sqrt[3]{9}$ です。根号を外すために、それぞれを6乗すれば、 $729, 125, 81$ となります。よって、\[ 3\gt \sqrt{5}\gt \sqrt[3]{9} \]となることがわかります。

ここで、底は $2$ で、1より大きいことから、真数が大きいほど対数が大きいことがわかります。対数関数のグラフで、底が1より大きいときのグラフを見ればわかりますね。 $y=\log_a x$ で、 $x$ が大きいほど、 $y$ は大きくなっています。そのため、真数の大きさの順番が対数の大きさの順番となるので、小さい順に並べると\[ \log_8 9,\ \log_4 5, \ \log_2 3 \]となることがわかります。

(2)も底を合わせましょう。 $0.5$ に合わせると
\begin{eqnarray} \log_{0.25} 3 &=& \frac{\log_{0.5} 3}{\log_{0.5} 0.25} \\[5pt] &=& \frac{1}{2}\log_{0.5} 3 \\[5pt] &=& \log_{0.5} \sqrt{3} \\[5pt] \end{eqnarray}となります。3つ目も、無理やり対数で表して、真数がわかるようにしてみましょう。 \begin{eqnarray} -1 &=& -\log_{0.5} 0.5 \\[5pt] &=& \log_{0.5} (0.5)^{-1} \\[5pt] &=& \log_{0.5} 2 \\[5pt] \end{eqnarray}となります。

底が同じになったので、違いは真数だけです。真数の小さい順に並べると、 $\sqrt{3},2,3$ となることがわかります。ただ、今考えている対数の底は、 $0.5$ であり、1より小さいんですね。ここが先ほどの(1)とは異なるところです。底が1より小さいときの対数関数のグラフを見てみましょう。 $y=\log_a x$ のグラフは、 $x$ が小さいほど $y$ は大きくなります。つまり、小さい順に並べると\[ \log_{0.5} 3,\ \log_{0.5} 2, \ \log_{0.5} \sqrt{3} \]となります。