【基本】平面上での内分点と外分点

ここでは、平面上で、内分点と外分点の座標がどうなるかを見ていきます。

平面上での内分点と外分点

【基本】数直線上の内分点と外分点では、数直線上での内分点と外分点を考えました。平面の場合も、定義は同じです。数直線のときと同じですが、もう一度書いておきます。

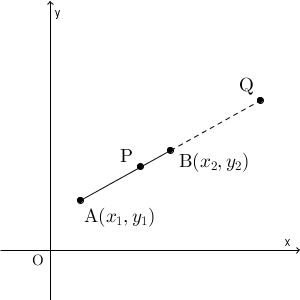
これは、 $m\gt n$ のとき、 P が、線分 AB を $m:n$ に内分する点、 Q が線分 AB を $m:n$ に外分する点の例となっています。

平面上の内分点と外分点の座標

さて、それでは、内分点と外分点の座標を求めてみましょう。

といっても、難しいことはありません。まずは、上の例で見たように、線分 AB が x 軸にも y 軸にも平行でない場合を考えます。このとき、次のように補助線をひいてみましょう。

A を通り x 軸に平行な直線を引き、それぞれの点から垂線をおろします。そして、交点には元の点に $'$ を追加した名前をつけます。

こうすると、 $\mathrm{ AP:PB }=m:n$ ならば、 $\mathrm{AP':B'P'}=m:n$ が成り立ちます（$\triangle\mathrm{APB}$ と $\triangle\mathrm{AP'B'}$ が相似だからです）。つまり、 $\mathrm{ P' }$ は、線分 $\mathrm{ AB' }$ を $m:n$ に内分する点になっている、ということです。

こうなれば、数直線のときと同じですね。【基本】数直線上の内分点と外分点の座標で見た内容を踏まえると、 $\mathrm{ P }$ の x 座標、つまり、 $\mathrm{ P' }$ の x 座標は、\[ \frac{nx_1+mx_2}{m+n} \]で求めることができます。外分のときも同様にして、 Q の x 座標が\[ \frac{-nx_1+mx_2}{m-n} \]で求められることがわかります。

縦についても同様のことが言えます。また、線分 AB が x 軸や y 軸に平行な場合も含め、次のようにまとめられることがわかります。

もし、線分 AB が x 軸に平行ならば、 $y_1=y_2$ なので、上の内分点の式も外分点の式も y 座標は $y_1$ と一致するのであってますね。また、 x 座標は数直線上のときと同じ話なので、上の場合にまとめられる、というわけです。

具体的な計算をしてみましょう。 $\mathrm{ A }(2,-5)$, $\mathrm{ B }(-4,1)$ のとき、線分 AB を $2:1$ に内分する点の座標は
\begin{eqnarray} & & \left(\frac{1\cdot 2+2\cdot(-4)}{2+1}, \frac{1\cdot (-5)+2\cdot 1}{2+1}\right) \\[5pt] &=& \left(-2, -1\right) \\[5pt] \end{eqnarray}となります。また、線分 AB を $2:1$ に外分する点の座標は \begin{eqnarray} & & \left(\frac{(-1)\cdot 2+2\cdot(-4)}{2-1}, \frac{(-1)\cdot (-5)+2\cdot1}{2-1}\right) \\[5pt] &=& \left(-10, 7\right) \\[5pt] \end{eqnarray}となります。分子は、「AB を $2:1$ に分ける」という条件から、外側同士、内側同士を掛ける、と関連付けると覚えやすくなると思います。また、外分点の場合は、符号が変わっていることに注意しましょう。検算のために、簡単に図をかいてみると、符号の間違いなどのミスに気づきやすいです。

おわりに

ここでは、平面上で、内分点と外分点について考えました。数直線の話が使えるように分解することで、だいぶ扱いやすくなりましたね。座標の式の見た目はごついですが、それぞれは数直線での話で出てきた式なので、ビビらないようにしましょう。