【基本】数直線上の内分点と外分点

ここでは、数直線上で、内分点と外分点について見ていきます。

内分点と外分点

数直線上で、原点 O と、点 $\mathrm{A}(1)$ があるとします。

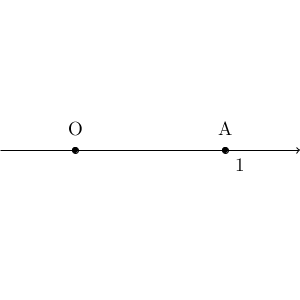
このとき、 $\mathrm{ OB:AB } = 2:1$ となる点 B はどこにあるでしょうか。

「OA を3分割して、左から2か所目を考えればいい」と思いつく人もいるでしょう。

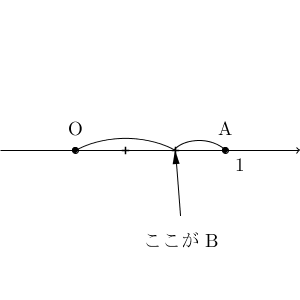
この図から、 B の座標は $\dfrac{2}{3}$ だとわかります。

しかし、注意が必要なのは、これだけではない、ということです。実は $\mathrm{ OB:AB } = 2:1$ となる点は、もう一つあります。どこにあるかわかるでしょうか。

この条件を満たすもう一つの点は、ここにあります。

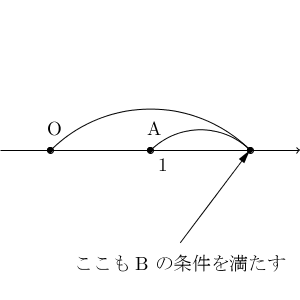
気付きにくいですが、外にあるんですね。 $\mathrm{ OB }=2$, $\mathrm{ AB }=1$ のときも、 $\mathrm{ OB:AB } = 2:1$ という条件を満たします。 $\mathrm{ OB:AB } = 2:1$ となる点 B の座標は、 $\dfrac{2}{3}$ と $2$ の2つあります。

このような「線分の端点からの距離が $m:n$ となっている点」は、今後もよく出てきます。ただ、そのような点は、ここで見た例のように、2つ該当することがあります。ですので、それぞれ別の呼び方があったほうが便利ですよね。このような点のうち、線分上にある点を内分点といい、線分上にない点を外分点といいます。

上の例でいえば、 $\left(\dfrac{2}{3}\right)$ の点が内分点、 $(2)$ の点が外分点ということです。また、 $1:1$ に外分する点はありません。線分 AB の延長線上の点 Q で、 $\mathrm{ AQ=QB }$ となることはないからです。

おわりに

ここでは、数直線上で、内分点と外分点について見てきました。ただ、これらの点の座標がわからなければ意味がありません。これらの求め方については、別のページ（参考：【基本】数直線上の内分点と外分点の座標）で解説します。