【基本】ベクトルの内積となす角

🕒 2017/08/28 🔄 2023/05/01

ここでは、ベクトルの成分がわかっているときに、内積からベクトルのなす角を求める方法について見ていきます。

📘 目次

ベクトルの内積となす角

例題

$\vec{a}=(2,-1)$, $\vec{b}=(3,1)$ のとき、 $\vec{a},\vec{b}$ のなす角を求めなさい。

ベクトルの成分しかわかっていません。成分が決まれば向きが決まるので、なす角も決まるはずですが、この2つは直接にはつながりません。しかし、実はベクトルの内積によってつながるんですね。順番に考えていきましょう。

【基本】ベクトルの内積と成分で見たように、ベクトルの成分から内積が出せるのでしたね。
\begin{eqnarray} \vec{a}\cdot\vec{b} &=& 2\cdot3+(-1)\cdot 1=5 \end{eqnarray}となります。

また、【基本】ベクトルの内積で見た通り、内積は、ベクトルの大きさとなす角を使って表すこともできます。なす角を $\theta$ とおけば
\begin{eqnarray} \vec{a}\cdot\vec{b} &=& |\vec{a}||\vec{b}|\cos\theta \\[5pt] &=& \sqrt{2^2+(-1)^2}\sqrt{3^2+1^2}\cos\theta \\[5pt] &=& 5\sqrt{2}\cos\theta \\[5pt] \end{eqnarray}となります。

この2つの式から
\begin{eqnarray} 5\sqrt{2}\cos\theta &=& 5 \\[5pt] \cos\theta &=& \frac{1}{\sqrt{2} } \\[5pt] \theta &=& 45^{\circ} \end{eqnarray}となります。これが答えです。

ちなみに、この問題は、図形的に解くこともできます。

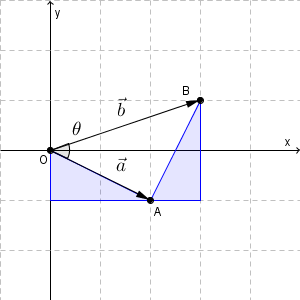
上の2つの青い直角三角形は、直角をはさむ辺の長さが $1$, $2$ なので、合同です。よって、三角形 OAB は直角二等辺三角形です。なので、この図を見てすぐにこのことに気づけば、計算しなくても $\theta=45^{\circ}$ だと求めることができます。

が、なかなか気づける人ばかりではありません。しかし、内積を使う方法なら、計算だけで求めることができます。強力な武器になりますね。問題文に「内積」という言葉は出てきていないので、自分で内積を使うことに気づく必要はありますが。

さて、上で見た方法を、一般的な形で書いておきましょう。

ベクトルのなす角

$\vec{0}$ でない2つのベクトル $\vec{a}=(a_1,a_2)$, $\vec{b}=(b_1,b_2)$ のなす角を $\theta$ とすると、次が成り立つ。
\begin{eqnarray} \cos\theta &=& \frac{\vec{a}\cdot\vec{b} }{|\vec{a}||\vec{b}|} \\[5pt] &=& \frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2} } \\[5pt] \end{eqnarray}

ベクトルの垂直

$\vec{0}$ でない2つのベクトル $\vec{a}=(a_1,a_2)$, $\vec{b}=(b_1,b_2)$ のなす角が $90^{\circ}$ のとき、2つのベクトルは垂直である、といいます。また、記号で $\vec{a}\perp\vec{b}$ と書きます。

内積の定義から考えると、 $\vec{0}$ でない2つのベクトルに対し、2つのベクトルが垂直であることと2つのベクトルの内積が $0$ であることが同値であることはわかるでしょう。また、上で見た内容から、\[ a_1b_1+a_2b_2=0 \]が成り立つこととも同値である、ということがわかります。

垂直であることを示す問題はよく出題されます。このとき、ベクトルを使って、内積が $0$ であることを示す、という解き方もよく使います。今後見ていくことになります。

ベクトルの垂直

$\vec{0}$ でない2つのベクトル $\vec{a}=(a_1,a_2)$, $\vec{b}=(b_1,b_2)$ について、次の3つは互いに同値である。