🏠 Home / 数学C / 平面上の曲線 / 二次曲線

【基本】双曲線と漸近線

🕒 2018/04/12 🔄 2023/06/22

ここでは、双曲線の漸近線についてみていきます。

📘 目次

双曲線と漸近線

【基本】双曲線の焦点（焦点がx軸上）などで見た通り、2つの点（焦点）からの距離の差が、0でない一定の値になる点の軌跡を、双曲線といいます。

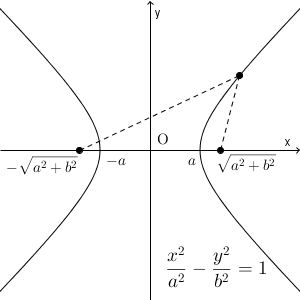
焦点が x 軸上にある場合、双曲線の方程式は\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \]となります（ $a,b\gt 0$ とします）。

このグラフを、もっとひいたところから見ると、次のようになります。

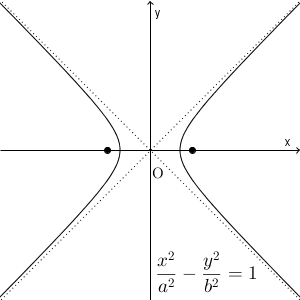
原点から遠ざかるにつれて、点線でかいた線に近づいていくことがわかります。思い出してみると、昔見た $y=\dfrac{a}{x}$ という形の双曲線も、 x 軸や y 軸に近づいていましたね。

このように、曲線がある直線に近づいていく場合、その直線のことを漸近線(asymptote) といいます。以下では、漸近線の方程式を見ていくことにしましょう。

双曲線の漸近線

まずは、 $x,y\gt 0$ の部分で考えましょう。残りの部分は対称性を使って同じように考えられますからね。

さて、 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ を満たす点で、 x 座標が $p$ のときを考えましょう。このときの y 座標を $q$ とすると
\begin{eqnarray} \dfrac{p^2}{a^2}-\dfrac{q^2}{b^2} &=& 1 \\[5pt] \dfrac{q^2}{b^2} &=& \dfrac{p^2}{a^2}-1 \\[5pt] q^2 &=& b^2\cdot \dfrac{p^2-a^2}{a^2} \\[5pt] \end{eqnarray}となります。また、 $q\gt 0$ の場合を考えているので、 \begin{eqnarray} q &=& \frac{b}{a}\sqrt{p^2-a^2} \end{eqnarray}となります。よって、原点とこの点 $(p,q)$ を結んだ直線の傾きは \begin{eqnarray} \frac{q}{p} &=& \frac{b}{a}\sqrt{1-\dfrac{a^2}{p^2} } \end{eqnarray}となります。右辺は、 p を大きくしていくとルートの中が $1$ に近づいていきます。よって、上の図と合わせて考えれば、漸近線は $y=\dfrac{b}{a}x$ ではないか、と考えられます。

実際、2点 $\left(p,\dfrac{b}{a}p\right)$ と $(p,q)$ について考えてみましょう。 $y$ 座標の差は
\begin{eqnarray} & & \dfrac{b}{a}p-q \\[5pt] &=& \dfrac{b}{a}p-\frac{b}{a}\sqrt{p^2-a^2} \\[5pt] &=& \frac{b}{a}\times\left(p-\sqrt{p^2-a^2}\right)\times\frac{p+\sqrt{p^2-a^2} }{p+\sqrt{p^2-a^2} } \\[5pt] &=& \frac{b}{a}\times\frac{a^2}{p+\sqrt{p^2-a^2} } \\[5pt] \end{eqnarray}となります。分母にある $p$ の影響で、 p を大きくしていくと、 y 座標の差は $0$ に近づいていくことがわかります。このことから、双曲線は $y=\dfrac{b}{a}x$ に近づいていくことがわかります。

対称性から、上下・左右に反転した場合も同じように考えられるため、 $y=\dfrac{b}{a}x$ , $y=-\dfrac{b}{a}x$ の2つが双曲線の漸近線であることがわかります。

この2つを変形すると、次のように書き換えることができます。\[ \frac{x}{a}-\frac{y}{b}=0,\ \frac{x}{a}+\frac{y}{b}=0 \]よくみると、この2つの左辺は、双曲線の方程式\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \]の左辺を因数分解したときに出てくる式ですね。

なお、【基本】双曲線の焦点（焦点がy軸上）でみた、焦点が y 軸上にある双曲線の場合も同様です。\[ -\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1 \]の漸近線は\[ \frac{x}{a}-\frac{y}{b}=0,\ \frac{x}{a}+\frac{y}{b}=0 \]となります。上で見たように直接確かめることもできますし、因数分解をしたときに同じ式が出てくることからも予想できるでしょう。

直角双曲線

$a=b$ のときは、先ほど求め双曲線の漸近線は\[ \frac{x}{a}-\frac{y}{a}=0,\ \frac{x}{a}+\frac{y}{a}=0 \]となります。これは、書き換えれば、 $y=x$, $y=-x$ の2つです。これらは直交します。このように、漸近線が直交する双曲線のことを、直角双曲線といいます。