🏠 Home / 数学II / 図形と方程式 / 直線と方程式

【基本】直線の方程式（一般形）

🕒 2017/07/20 🔄 2023/05/01

ここでは、直線の方程式の一般形について見ていきます。どんな直線の方程式も表すことができる方程式について考えていきます。

📘 目次

図形の方程式

過去に、一次関数や二次関数のグラフを扱ったことがありましたね。 y が x の関数であるとは、 x を決めたときに y が1つに決まることをいいます。この対応をそれぞれの点で表現したものを関数のグラフというのでした。

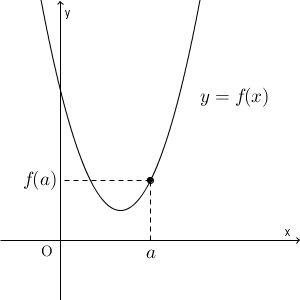
ここからは、逆に、図形に対して、式を対応させることを考えたいと思います。こうすることで、いろいろな図形の問題を、座標を使った計算によって求めることができるようになり、考えやすくなることがあります。

ただ、少しだけ問題があります。というのも、関数からグラフを対応させるのは、 x に値を代入して y を求め、それらに対応する点をとり、つなげていけば終わりですが、逆はそうはいきません。図形に対応する関数がうまく見つかるとは限りません。

例えば、「原点が中心で半径が 1 の円」に対応する関数を考えてみましょう（今後扱います）。 x を決めても、対応する y が2つあり、1つに決まらないこともあります。関数の形ではかけないものもあるんですね。

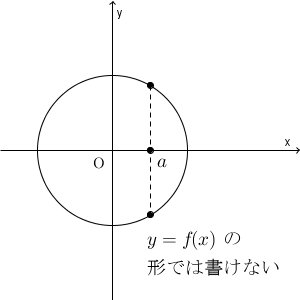
ただ、方程式の形だと、うまく表現できる場合があります（実際、円に対応する方程式はあります。後で見ることになります）。

ある図形に対して、その図形を構成する各点 $(x,y)$ が、ある方程式を満たし、逆に、その方程式を満たす数字の各組 $(x,y)$ がその図形に含まれる点であるとき、この方程式を、図形の方程式といいます。また、この図形のことを、方程式の表す図形といいます。

つまり、

図形上の点 $(x,y)$
方程式を満たす数の組 $(x,y)$

この2つの集合が完全に一致しているときに、図形と方程式を関連付ける、ということです。

なんだか難しそうな言い方ですが、まずは直線を例に見ていきましょう。

xとyの一次方程式が表す図形

方程式の中で、一番オーソドックスなものは、一次方程式です。一般的な形で書くと、\[ ax+by+c=0 \]となります。一次方程式を考えるので、 $a\ne 0$ または $b\ne 0$ です。

例えば、 $a=2,b=1,c=-3$ とすると、代入して移行すれば $y=-2x+3$ となります。この形は今までよく使ってきたので、なじみがありますね。傾きが $-2$ で切片が $3$ の直線です。

また、 $a=0,b=2,c=3$ としてみましょう。今度は、 $y=-\dfrac{3}{2}$ となります。これは y座標が固定で、 x は何でもいい、ということです。そのため、これを満たす点をすべて集めると、 $\left(0,-\dfrac{3}{2}\right)$ を通り、 x 軸に平行な直線となります。

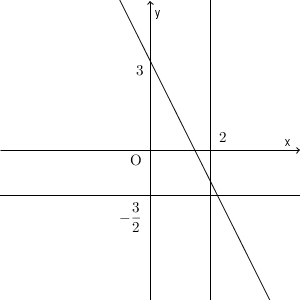
最後に、 $a=1,b=0,c=-2$ としてみましょう。 $x=2$ となります。このとき、この式の表す図形は、 $(2,0)$ を通り、 y 軸に平行な直線となります。今まで一次関数のグラフを扱ってきましたが、 y 軸に平行な直線はなかったですよね。しかし、上のように $ax+by+c=0$ という形で書けば、 y 軸に平行な直線も、この式に含まれるようになります。

これらをより一般化したものを、次で考えましょう。

直線の方程式の一般形

先ほどは、\[ ax+by+c=0 \]の係数に試しに値を入れてみたところ、いくつかの直線の方程式が得られました。ここでは、いつでも直線の方程式が得られるのかどうか、そして逆に、どの直線もこの方程式の形で書けるのかどうかを考えてみましょう。

まず、上の方程式が、必ず直線の方程式を表すのかどうかを考えてみましょう。 $b\ne 0$ のときは\[ y=-\frac{a}{b}x-\frac{c}{b} \]と変形できるので、傾きが $-\dfrac{a}{b}$ で、切片が $-\dfrac{c}{b}$ の直線になることがわかります。 $b=0$ のときは、$a\ne 0$ なので\[ x=-\frac{c}{a} \]と変形できます。これは y 軸に平行な直線です。よって、どの場合も、直線を表すことがわかります。

逆に、どの直線もこの方程式の形で書けるかどうかを考えます。直線が y 軸と交わっていないときは、 y 軸と平行ということです。よって、 x 軸との交点を $(p,0)$ とすると、方程式は $x-p=0$ と書けます。これは、 $a=1,b=0,c=-p$ とした場合と考えられます。

y 軸と1点で交わっている場合は、その点を $(0,n)$ とし、傾きを m とすれば、この直線の方程式は $y=mx+n$ となります。これは\[ -mx+y-n=0 \]と変形できるので、 $a=-m, b=1,c=-n$ とした場合だと考えられます。 $ax+by+c=0$ の形で表現できるということですね。

まとめると、\[ ax+by+c=0 \]を満たす点の集合は直線を表し、どの直線もこの形の方程式で表されることがわかりました。このため、この方程式を、直線の方程式の一般形と呼びます。

今までよく使っていた $y=mx+n$ の形も直線の方程式と言いますが、こちらは、 y 軸に平行な直線が表現できないことに注意しましょう。