【基本】楕円の焦点(焦点がx軸上)
ここでは、【基本】楕円の焦点(具体例)で見た内容を、一般的な内容で見ていきます。
楕円の焦点
この軌跡は、「2点からの距離の和が一定の点の集まり」のことです。【基本】楕円の焦点(具体例)で見た内容の一般化です。
この軌跡上の点を $(x,y)$ として、この点が満たす方程式を考えます。
この点と、 $(-p,0)$, $(p,0)$ からの距離の和が $2a$ なので
\begin{eqnarray}
\sqrt{(x+p)^2+y^2}+\sqrt{(x-p)^2+y^2} &=& 2a \\[5pt]
\sqrt{(x+p)^2+y^2} &=& 2a-\sqrt{(x-p)^2+y^2}
\end{eqnarray}となります。この両辺を2乗すれば
\begin{eqnarray}
(x+p)^2+y^2 &=& 4a^2-4a\sqrt{(x-p)^2+y^2}+{(x-p)^2+y^2} \\[5pt]
4px &=& 4a^2-4a\sqrt{(x-p)^2+y^2} \\[5pt]
a^2-px &=& a\sqrt{(x-p)^2+y^2}
\end{eqnarray}となり、さらに2乗すれば
\begin{eqnarray}
a^4-2a^2px+p^2x^2 &=& a^2x^2-2a^2px+a^2p^2+a^2y^2 \\[5pt]
(a^2-p^2)x^2+a^2y^2 &=& a^2(a^2-p^2) \\[5pt]
\end{eqnarray}となります。ここで、$a^2\gt p^2$ なので、 $b=\sqrt{a^2-p^2}$ とおけば、上の式は
\begin{eqnarray}
b^2x^2+a^2y^2 &=& a^2b^2 \\[5pt]
\frac{x^2}{a^2}+\frac{y^2}{b^2} &=& 1 \quad \cdots (*)
\end{eqnarray}となります。
逆に、この式を満たしているとき、
\begin{eqnarray}
y^2
&=&
b^2 \left(1-\frac{x^2}{a^2}\right) \\[5pt]
&=&
(a^2-p^2) \times \frac{a^2-x^2}{a^2} \\[5pt]
\end{eqnarray}が成り立ちます。この値は0以上なので、 $|x|\leqq a$ であることがわかります。また、
\begin{eqnarray}
& &
\sqrt{(x+p)^2+y^2} \\[5pt]
&=&
\frac{1}{a}\sqrt{a^2(x+p)^2+(a^2-p^2)(a^2-x^2)} \\[5pt]
&=&
\frac{1}{a}\sqrt{2a^2xp+a^4+p^2x^2} \\[5pt]
&=&
\frac{1}{a}\sqrt{(a^2+px)^2} \\[5pt]
&=&
\frac{1}{a}|a^2+px| \\[5pt]
\end{eqnarray}となります。同様の計算から
\begin{eqnarray}
& &
\sqrt{(x-p)^2+y^2} \\[5pt]
&=&
\frac{1}{a}|a^2-px| \\[5pt]
\end{eqnarray}となります。なお、 $|x|\leqq a$ であり、 $p\lt a$ なので、
\begin{eqnarray}
& &
\sqrt{(x+p)^2+y^2}+\sqrt{(x-p)^2+y^2} \\[5pt]
&=&
\frac{1}{a}|a^2+px|+\frac{1}{a}|a^2-px| \\[5pt]
&=&
\frac{1}{a}(a^2+px)+\frac{1}{a}(a^2-px) \\[5pt]
&=&
2a
\end{eqnarray}となり、 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ を満たすすべての点が、条件を満たすことがわかりました(2乗している箇所で、両辺が正になっていることを確かめる方法でもいいです)。なので、これが答えとなります。
なお、次の円の方程式と見比べてみましょう。\[ x^2+y^2=a^2 \]これは、原点を中心とした半径 $a(\gt 0)$ の円の方程式です。これを変形すれば\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2} = 1\]となり、先ほど求めた式とかなり似ていますね。 $y^2$ の分母が違うだけです。このことは、楕円が円を y 軸方向に拡大・縮小したものであることを表しています(この性質は、別のところで詳しく見ます)。
上で出てきた2点を楕円の焦点(focus) といいます。途中で $b=\sqrt{a^2-p^2}$ とおきましたが、これを変形すれば $p=\sqrt{a^2-b^2}$ となるので、焦点の座標はこれを使って表すことができます。
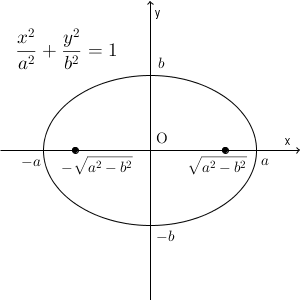
長軸の長さは $2a$, 短軸の長さは $2b$ となり、楕円上の点から2つの焦点までの距離の和は $2a$ となります。用語は、【基本】楕円の焦点(具体例)に出ています。
おわりに
ここでは、ある2点からの距離の和が一定の点の集まりが楕円になることをみました。円と似た式が得られること、楕円の方程式と焦点の座標との関係をおさえておきましょう。





