【基本】標本平均の分布と正規分布

ここでは、標本平均の分布と正規分布の関係について見ていきます。

標本平均の分布と正規分布

【基本】標本平均の分布で見たように、母平均 $m$、母標準偏差 $\sigma$ の母集団から大きさ $n$ の標本を復元抽出したとき、標本平均 $\bar{X}$ の期待値（平均）は $m$ で標準偏差は $\dfrac{\sigma}{\sqrt{n}}$ となるのでした。

このことから、 $n$ を大きくしていくと、バラツキが減っていき、期待値に近い値をとる確率が高くなっていくことがわかります。

ここで、$n$ を大きくしていったときに、具体的に標本平均の分布がどう変わるかを見てみましょう。

上のリンク先と同じように、0, 1, 2, 3 と書かれたカードが、それぞれ、4, 3, 2, 1 枚ずつあるとします。この10枚のカードを母集団とし、このカード全体から1枚を引いて元に戻す、という操作を $n$回やることにします。 $n=1$ のときは、標本平均 $\bar{X}$ の分布は、母集団分布と同じで、次のようになります。高さが確率を表しています。

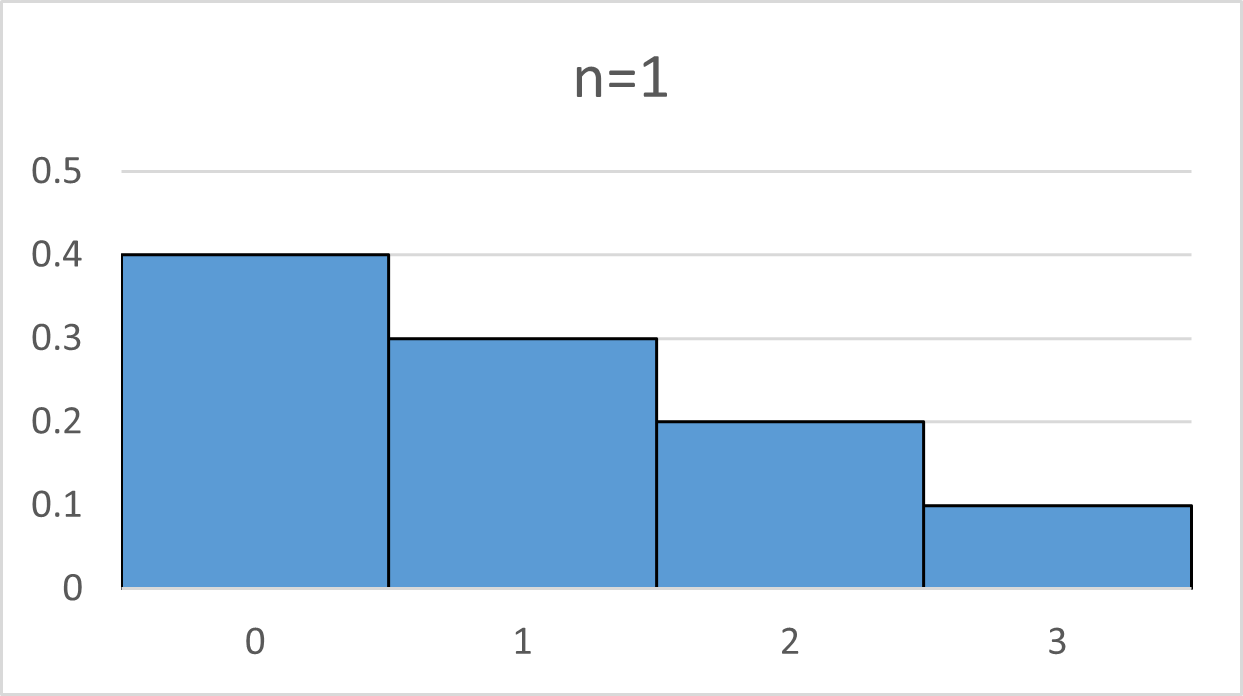
$n=2,4,8,16$ と増やしていくと、標本平均 $\bar{X}$ の分布は次のように変化していきます。先ほどと同様に、高さが確率を表しています。

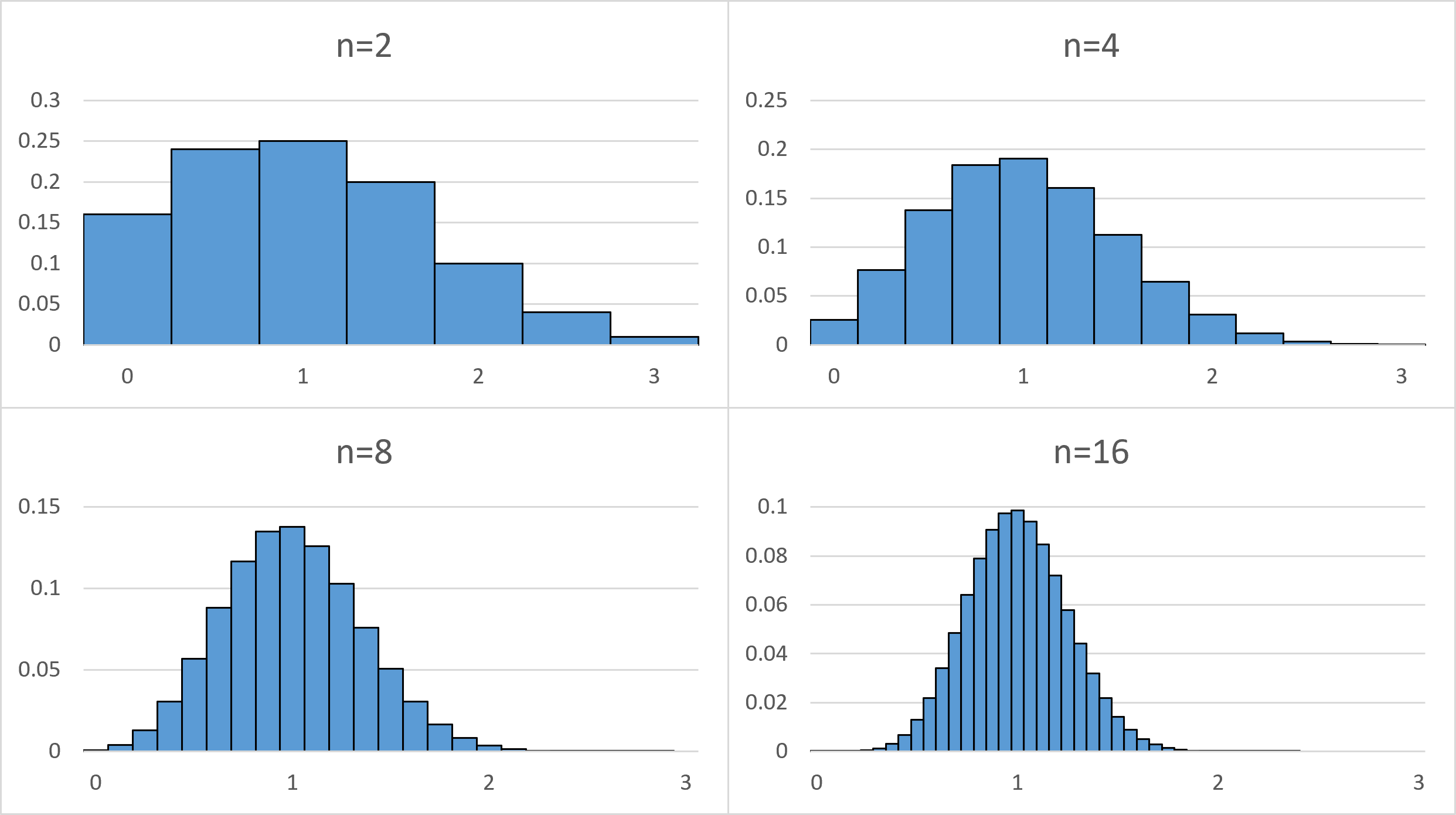
なんだか見たことがある形に近づいてきましたね。【基本】正規分布で見た正規分布の分布曲線に似ています。

$n=16$ のときと正規分布の分布曲線とを並べてみます。正規分布は、平均が $1$ で分散が $\dfrac{1}{16}$ のものです。 $\bar{X}$ の平均と分散に合わせています。

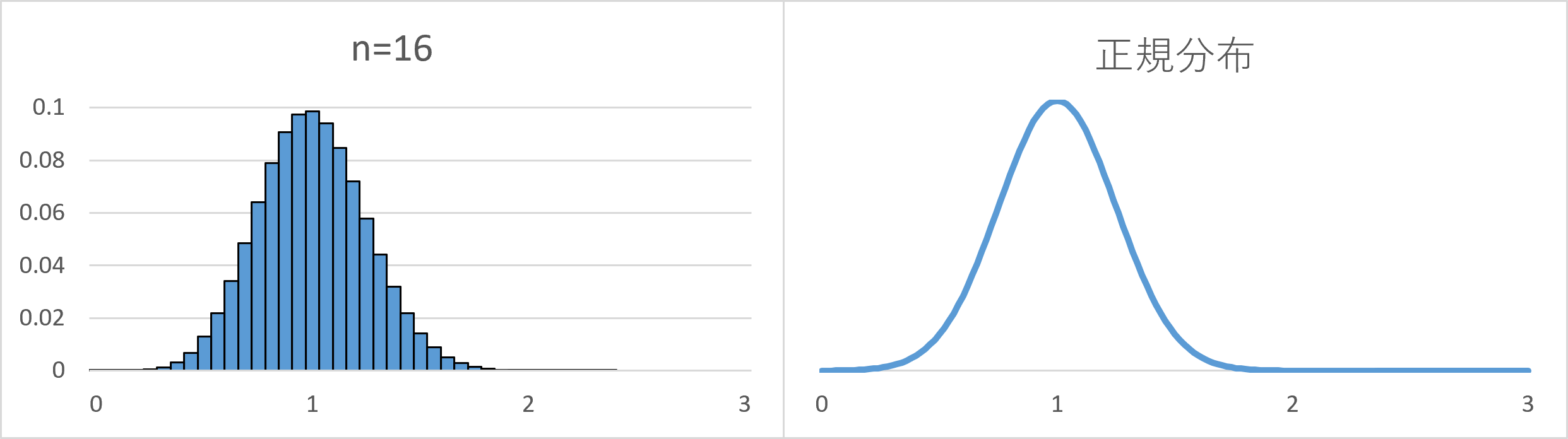
重ね合わせるともっとよくわかるのですが、重ね合わせるためには少し変形が必要です。連続型確率変数の分布曲線は確率と面積が対応するようになっています。離散型も確率と面積が対応するようにするには、長方形の横の長さが $\dfrac{1}{16}$ 倍になった分、縦の長さを $16$ 倍しておく必要があります。

このように変形してから両者を重ね合わせると、次のようになります。

かなり近いですね。 $n=1$ のときは、山のような形とはまったく異なっていたのに、標本平均の分布を考えると、正規分布に近づいていくんですね。

実は、他の場合でも正規分布に近づいていくことが知られています。

これは高校範囲では証明することは難しいですが、問題を解くときには使ってもかまいません。「十分大きい」がどれくらいかはケースによりますが、過去の共通テストなどを見ると、数百くらいであれば十分大きいと考えているようです。また、近似することを想定している場合には問題文中に「正規分布で近似する」と書かれていることが多いです。

そのほかの細かいこと

先ほど、標本の大きさ $n$ が十分大きければ、標本平均は正規分布で近似できることを見ました。このときに、標本を無作為抽出するのですが、実は、暗に、復元抽出することを想定していました。

なぜなら、標本平均の分散の計算では、標本の変量が独立であることを使っていたからです。復元抽出の場合は独立なので問題ないですが、非復元抽出の場合は独立とは限らないため、分散が $\dfrac{\sigma^2}{n}$ となるかはわかりません。

しかし、母集団の大きさが十分大きい場合は、復元抽出と非復元抽出との差はすごく小さくなります。そのため、非復元抽出の場合でも、$n$ が十分大きく、$n$ に比べて母集団が十分大きい場合には、近似的に、標本平均の分布は正規分布に従うとみなすことができます。

また、これも高校範囲では示せないことですが、独立な正規分布同士の和は正規分布になることが知られています。もう少しちゃんと書くと、 $X_i,X_j$ が正規分布に従い、互いに独立であるとき、 $X_i+X_j$ も正規分布に従う、ということです（ちなみに、平均・分散が同じである必要はありません）。

このことから、母集団分布が正規分布 $N(m,\sigma^2)$ に従うときは、$n$ が大きくなくても、標本平均は正規分布 $N \left(m,\dfrac{\sigma^2}{n} \right)$ に従います。

このことを使った問題が大学入試で出題されることは少ないと思いますが、知識として知っておくといいでしょう。

おわりに

ここでは、標本の大きさが十分大きいとき、標本平均の分布が正規分布で近似できることを見ました。この後で学ぶ母平均の推定では、このことを利用します。