【基本】平面上の2点間の距離

🕒 2017/07/11 🔄 2023/05/01

【基本】数直線上の2点間の距離では、数直線上での2点間の距離について見ました。ここでは、平面上の2点間の距離について見ていきます。一次元から二次元の話に変わります。

📘 目次

座標平面

座標平面について復習します。ただ、いろいろ細かいことも書いているので、ここは飛ばして、2点間の距離のところに進んでも構いません。今まで使っていたものを、改めて見ているだけですので。

さて、平面上の各点に、2つの実数を対応させることを考えます。こうすることで、図形を計算で扱うことができるようになります。

まず、平面上に、左右に伸びる x 軸と、それに直交して上下に伸びる y 軸を引きます。

2軸の交点を原点と呼び、 O で表します。平面上のそれぞれの点について、原点から右にどれだけ移動し、上にどれだけ移動したものかが決まるので、各点とこの2つの実数とを対応させます。この2つの実数の組を、その点の座標と言います。そして、各点に座標を対応させた平面のことを、座標平面といいます。

座標を与える方法を座標系と言いますが、上のように直交する2つの軸をもとに作る座標系のことを、直交座標系と言います。こう書くと、「他にも座標のとり方があるのかな？」と思う人もいるかもしれませんが、実はあります。複素数平面の分野では、原点からの距離と角度を使って表す極座標系というものも使います。また、軸が斜めに交わっている、斜交座標系というものもあります。ただ、当面は直交座標系しか出てきません。

平面上の2点間の距離

それでは、平面上での2点間の距離について考えましょう。すでに知っている人も多いですが、改めて考えてみます。

$\mathrm{ P }(x_1,y_1)$, $\mathrm{ Q }(x_2,y_2)$ の2点間の距離を求めてみましょう。

PQ が x 軸に平行な場合や y 軸に平行な場合は、簡単ですね。本質的には、【基本】数直線上の2点間の距離と同じ、一次元の話です。 x 軸に平行な場合は $|x_2-x_1|$ となり、 y 軸に平行な場合は $|y_2-y_1|$ となります。なので、上の図のように、どちらとも平行でない場合を考えましょう。

ノーヒントだと少し難しいかもしれませんが、すでにどうやって求めるかは知っている人がほとんどでしょう。忘れてしまった人も、次のように線を引いてみると、思い出すかもしれません。

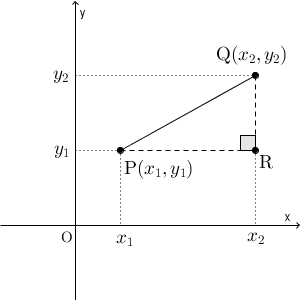
二次元だと話がややこしいので一次元の話に分割するため、このような線を引くことは多いんですね。 P を通り x 軸に平行な直線と、 Q を通り y 軸に平行な直線を引き、その交点を R とします。すると、三角形 PQR は直角三角形になります。

また、 PR の長さは $|x_2-x_1|$ であり、 QR の長さは $|y_2-y_1|$ であるため、三平方の定理から
\begin{eqnarray} \mathrm{ PQ } = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \end{eqnarray}となることがわかります。ここでは、 $|a|^2=a^2$ であることを使っています。

よく考えれば、 PQ が x 軸に平行な場合や y 軸に平行な場合も、この式が使えることがわかります。例えば x 軸に平行な場合は、 $y_2-y_1=0$ になるので
\begin{eqnarray} \mathrm{ PQ } = \sqrt{(x_2-x_1)^2} \end{eqnarray}となりますが、これは $|x_2-x_1|$ と同じですからね。

以上より、次の結果が得られます。

平面上の2点間の距離

2点 $\mathrm{ P }(x_1,y_1)$, $\mathrm{ Q }(x_2,y_2)$ の距離 PQ は次の式で表すことができる。\[ \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \]

このことから、原点との距離もすぐにわかります。例えば、 OP は、\[ \sqrt{x_1^2+y_1^2} \]となります。このこともよく使います。

ずっと「2点間の距離」と書いてきましたが、問題によっては、例えば「辺 PQ の長さ」や「線分 PQ の長さ」といった表現になっていることもあります。言い方が変わっているだけで、2点間の距離であることに違いはありません。