【基本】原点と直線との距離
ここでは、原点と直線との距離がどうなるかを考えていきます。
どういうときに点と直線との距離を考えるか
例えば、三角形 ABC の面積を求めるとするじゃないですか。こういう問題は今までよく出てきましたよね。このとき、 A から BC に垂線をおろし、その長さを求めれば、「底辺×高さ÷2」で面積が求められます。
今、この3点の座標がわかっているとして、同じことをしようとすると、垂線の長さをどうやって求めればいいのか、という問題が出てきます。
「三角形の高さ」に限らず、ある点からある直線に垂線をおろし、その垂線の長さを求める、ということはよくあります。この長さは、「点と直線との距離」とも言えます。
以下では、特殊なケースとして、原点からの距離について見ていきます。
原点と直線との距離
原点 $\mathrm{ O }(0,0)$ と、直線 $ax+by+c=0$ との距離を求めましょう。直線の方程式は一般形で書いておきます。
この直線が x 軸に平行なとき、つまり、 $a=0$ のときは、原点と直線との距離は $\left|\dfrac{c}{b}\right|$ となります。また、 y 軸に平行なとき、つまり、 $b=0$ のときは、原点と直線との距離は $\left|\dfrac{c}{a}\right|$ となります。これらは特殊な状況なので、すぐに求められます。
以下では、この直線が x 軸とも y 軸とも平行でないとします。 $a\ne 0$, $b\ne 0$ ということですね。
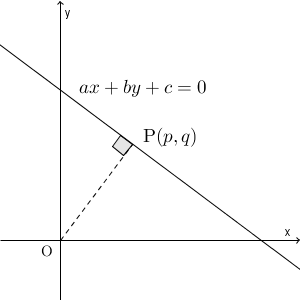
原点からこの直線に垂線をおろし、この直線との交点を $\mathrm{ P }(p,q)$ としましょう。この直線の方程式は\[ y=-\frac{a}{b}x-\frac{c}{b} \]と書くことができます。【基本】垂直な直線の方程式で見た内容から、垂直に交わる直線の傾きの積は $-1$ になることので、 OP の傾きは $\dfrac{b}{a}$ となることがわかります。また、これは原点を通るので、直線 OP の式は\[ y=\frac{b}{a}x \]となります。
以上から、次の2つの式が成り立ちます。\[ ap+bq+c=0, \quad q=\frac{b}{a}p \]2つ目の式を1つ目の代入すると
\begin{eqnarray}
ap+b\cdot\frac{b}{a}p+c &=& 0 \\[5pt]
\frac{a^2+b^2}{a}p &=& -c \\[5pt]
p &=& -\frac{ac}{a^2+b^2} \\[5pt]
\end{eqnarray}が得られます。これを2つ目の式に代入すると
\begin{eqnarray}
q &=& -\frac{bc}{a^2+b^2} \\[5pt]
\end{eqnarray}が得られます。
以上から、 OP の2乗は
\begin{eqnarray}
& &
\left(-\frac{ac}{a^2+b^2}\right)^2 +\left(-\frac{bc}{a^2+b^2}\right)^2 \\[5pt]
&=&
\frac{a^2c^2+b^2c^2}{(a^2+b^2)^2} \\[5pt]
&=&
\frac{c^2}{a^2+b^2} \\[5pt]
\end{eqnarray}となるため、原点と直線との距離 OP は\[ \frac{|c|}{\sqrt{a^2+b^2} } \]で求められることがわかります。
この式は、 $a=0$ や $b=0$ のときにも成り立ちますね。例えば、 $a=0$ とすると、上の式は $\dfrac{|c|}{\sqrt{b^2} }$ となりますが、これは事前に考えていた $\left|\dfrac{c}{b}\right|$ と等しいです。このことから、次のようにまとめることができます。
例えば、原点と直線 $3x+4y+5=0$ との距離は\[ \frac{5}{\sqrt{3^2+4^2} }=1 \]と求められます。
また、原点と直線 $y=mx+n$ との距離は、この直線の方程式を一般形にして $-mx+y-n=0$ としてから\[ \frac{|n|}{\sqrt{m^2+1} } \]で求めることができます。
おわりに
ここでは、原点と直線との距離を求めました。原点以外の場合はもう少し式が複雑になります。この場合は別のページ(参考:【標準】点と直線との距離)で見ることにします。





