【基本】円に内接する四角形

ここでは、円に内接する四角形の性質を見ていきます。

円に内接する多角形

次の図のように、多角形のすべての頂点が1つの円周上にあるとき、この多角形は円に内接する(inscribe) といいます。円の内側で接するので内接、ということです。

また、円を主語にして、「この円はこの多角形の外接円」ということもあります。多角形の外で接している円、ということですね。

三角形には必ず外接円が存在します。しかし、三角形以外の場合は外接円が存在するとは限りません。

円に内接する四角形

以下では、四角形が円に内接する場合、どのような性質を持っているか見ていきます。

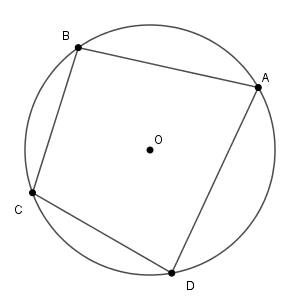
上の図のように、四角形 $\mathrm{ABCD}$ が円 $\mathrm{O}$ に内接しているとします。このとき、$\angle \mathrm{BAD}$ を $\alpha$, $\angle \mathrm{BCD}$ を $\beta$ とします。

ここで、円周角の定理を使います。以下のような内容です。中学のときに習っているはずです。

この円周角の定理から、弧 $\mathrm{BCD}$, 弧 $\mathrm{BAD}$ に対する中心角の大きさは、それぞれ $2\alpha$, $2\beta$ になることがわかります。

ここで、 $2\alpha+2\beta=360^{\circ}$ なので、\[ \alpha +\beta = 180^{\circ} \]が成り立ちます。

$\angle \mathrm{A}+\angle \mathrm{C}=180^{\circ}$ なので、自動的に、 $\angle \mathrm{B}+\angle \mathrm{D}=180^{\circ}$ も言えます。

四角形で、ある内角に向かい合う内角を対角といいます。なので、上の内容は、「対角の和は $180^{\circ}$ 」ということができます。

また、 $\angle \mathrm{C}$ の外角の大きさは $180^{\circ}-\beta=\alpha$ とも表せるので、「内角は、その対角の外角に等しい」こともいえます。

これらは円に内接する四角形が、必ず持っている性質です。

この性質を用いて、問題を解いてみましょう。

円に内接する四角形を使った例題

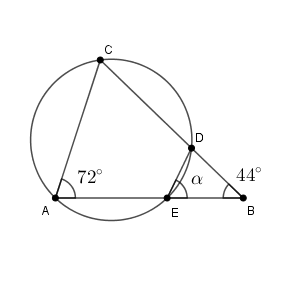
どの角に注目するかによって、複数の解き方があります。

例えば、 $\angle \mathrm{BDE}$ は $\angle \mathrm{A}$ の対角の外角なので、 $72^{\circ}$ です。なので、\[ \alpha=180^{\circ}-72^{\circ}-44^{\circ}=64^{\circ} \]と求めることができます。

また、三角形 $\mathrm{ABC}$ で考えて $\angle \mathrm{C}$ を求め、それが $\alpha$ と等しいことを利用して求めることもできるでしょう。

なお、この問題では使いませんでしたが、上の図で $\triangle \mathrm{BDE}$ と $\triangle \mathrm{BAC}$ は相似になります。円に内接する四角形の性質を使い、相似な図形を見つけて利用する問題もあります。

おわりに

ここでは、円に内接する四角形の性質を見ました。頂点と円の中心を結び、円周角の定理を使うことで、「対角の和は $180^{\circ}$ 」などの性質を持つことを見ました。これにより、角度がわかるようになったり、相似な図形を見つけることができるようになります。