【基本】関数の連続性

ここでは、関数の連続性について見ていきます。

関数の連続性

【基本】片側極限では、ガウス記号を用いた関数 $f(x)=\lbrack x\rbrack$ について考えました。ガウス記号は、「その数字を超えない最大の整数」を表す記号なので、この関数のグラフは次のようになります。

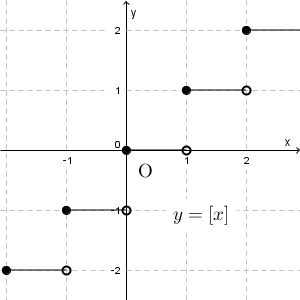
このグラフは、今までに見てきたいろんな関数のグラフと比べると、少し変わっていますね。グラフがたくさんのところで切れてしまっています。今まで学んできた関数（ $y=x^2$ とか $y=\sin x$ とか）のグラフは1つの曲線でつながっていて、このような切れているグラフとはなっていませんでした。

グラフがある場所でつながっているか切れているかは、重要な情報なので、このことを表す名前があります。つながっている場合は、連続(continuous) といい、つながっていない場合は、不連続(discontinuous) といいます。「ある場所でグラフがつながっている」というのを、もう少し数学的に書くと、次のように極限を使った表現になります。

この内容は、 $x$ が $a$ より小さい方から近づけていっても、大きい方から近づけていっても、 $f(x)$ は $f(a)$ に近づいていく、というです。これは、グラフが $x=a$ のところでつながっていることと対応します。

さきほどのガウス記号を使った関数 $f(x)=\lbrack x\rbrack$ をもう一度考えてみましょう。

$x\to\dfrac{1}{2}$ とすると、このまわりでは $f(x)=0$ なので、 $x=\dfrac{1}{2}$ で連続であるといえます。一方、 $x\to 1$ のときは、左側極限が $0$ で右側極限が $1$ であり、極限が存在しないので、 $x=1$ では不連続です。

極限が存在しても、不連続になることはあります。人工的な例ですが、次のような関数 $f(x)$ を考えてみましょう。
\begin{eqnarray} f(x) = \begin{cases} x^2 & ( x \ne 0 ) \\ 1 & ( x=0 ) \end{cases} \end{eqnarray} $x\to 0$ としたときに、 $f(x)\to 0$ となり、極限は存在します。しかし、 $f(0)=1$ なので、 $x\to 0$ としたときの極限と $f(0)$ の値は一致しません。よって、この関数は $x=0$ で不連続となります。実際、グラフも途切れています。

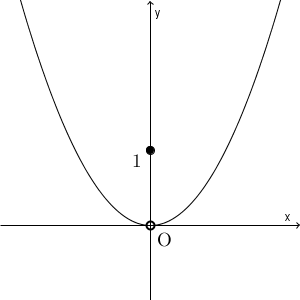
なお、 $f(x)=\sqrt{x}$ において、 $x=0$ が連続かどうかを考える場合には、定義されていない方から近づけることはできないため、\[ \lim_{x\to +0}f(x)=f(0) \]かどうかをチェックすることになります。実際、この式は成り立つので、 $f(x)=\sqrt{x}$ は、 $x=0$ で連続である、と言えます。

例題

(1)は、 $f(0)=0$ なので、 $x\to 0$ としたときに $f(x)\to 0$ となるかどうかを調べればいいですね。 $0\lt x \lt 1$ のときは、 $\lbrack x\rbrack=0$ なので、 $f(x)=0$ です。一方、 $-1\lt x \lt 0$ のときは、 $\lbrack x\rbrack=-1$ なので、 $f(x)=-x$ となり、 $x\to -0$ とすると $f(x)\to 0$ となることがわかります。よって、\[ \lim_{x\to 0}f(x)=f(0) \]が成り立つので、 $x=0$ で連続であることがわかります。

(2)は、 $f(x)=\lbrack \cos x\rbrack$ だから、 $f(0)=1$ です。また、 $0\lt x \lt \dfrac{\pi}{2}$ のときは、 $0\lt \cos x\lt 1$ なので、 $\lbrack \cos x\rbrack=0$ だから、 $x\to +0$ としたとき、 $f(x)\to 0$ となります。よって、 $x\to 0$ としたときの極限が $f(0)$ になることはないので、 $x=0$ で不連続であることがわかります。

実際、グラフをかくと次のようになります。

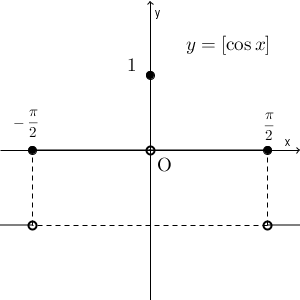
グラフからも、 $x=0$ のところで途切れていることがわかります。

おわりに

ここでは、関数の連続性について見ました。「グラフがつながっている」ことを、極限を使って表現しました。ある場所で連続かどうかを調べるには極限を求める必要があるので、極限の計算は復習しておきましょう。