【基本】積分を使って体積を求める

ここでは、積分を使って体積を求める方法を見ていきます。円すいの例を見た後に、一般の場合を見ていきます。

円すいの体積

座標空間で考えます。

$xy$ 平面上の3点、原点, $(h,0,0)$, $(h,r,0)$ を結んでできる直角三角形を考えます。ここで、$h,r$ は正の実数とします。この直角三角形を $x$ 軸を中心として回転させると円錐（えんすい）ができます。

この体積は、小学校のときに習いましたが、\[ \dfrac{1}{3}\pi r^2 h\]です。 $\pi r^2$ と $h$ はいいとしても、 $\dfrac{1}{3}$ は謎だし、唐突感があります。しかし、これは後で見るように、積分を使えばわかるようになります。

積分を使って面積を求める方法を見たときには、$x$ を少し動かしたときに面積がどう変わるかを考えたのでした（参考：【基本】面積と整式の不定積分）。体積でも同じように考えます。この円錐の高さが $x$ のときの体積を $V(x)$ で表すとして、 $V(x)$ を求めることにします。

この円錐を、2つの平面 $x=c$, $x=c+\Delta x$ で切ることにします。$\Delta x$ は正で、 $c$ も $c+\Delta x$ も、 $0$ 以上 $h$ 以下だとしましょう。

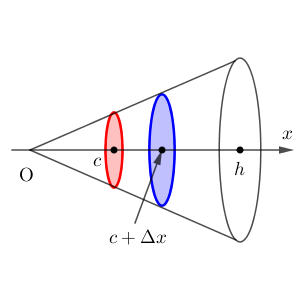
この2つ平面の間にある部分の体積を考えます。つまり、 $V(c+\Delta x)-V(c)$ のことですね。図でいうと、赤と青の円にはさまれた部分です。

これは、左端の切り口（赤い円）を底面とする高さ $\Delta x$ の円柱の体積よりも大きくなります。一方、右端の切り口（青い円）を底面とする円柱よりは小さくなりますね。

左端の円の半径を $r'$ とすると、元の直角三角形との比を考えれば\[ h:r=c:r' \]なので、\[ r'=\frac{cr}{h} \]となります。また、同様に考えると、右端の円の半径は $\dfrac{(c+\Delta x)r}{h}$ となります。

これらのことから、次のような不等式が成り立ちます。
\begin{eqnarray} & & \pi\left(\frac{cr}{h}\right)^2 \Delta x \lt V(c+\Delta x)-V(c) \lt \pi\left(\frac{(c+\Delta x)r}{h}\right)^2 \Delta x \\[5pt] & & \pi\left(\frac{cr}{h}\right)^2 \lt \frac{V(c+\Delta x)-V(c)}{\Delta x} \lt \pi\left(\frac{(c+\Delta x)r}{h}\right)^2 \\[5pt] \end{eqnarray}

ここで、最後の式の右辺で、 $\Delta x\to 0$ とすると、$\pi\left(\dfrac{cr}{h}\right)^2$ に収束し、左辺と一致します。このことから、はさみうちの原理により
\begin{eqnarray} V'(c) &=& \lim \frac{V(c+\Delta x)-V(c)}{\Delta x} \\[5pt] &=& \pi\left(\dfrac{cr}{h}\right)^2 \end{eqnarray}となることがわかります。これは、すべての $c$ で成り立つから、 $V(x)$ を微分したものが $\pi\left(\dfrac{cr}{h}\right)^2$ になることを表しています。

言い換えると、 $V(x)$ は $\pi\left(\dfrac{xr}{h}\right)^2$ を積分すれば求められる、ということです。そのため、
\begin{eqnarray} V(x) &=& \int_0^h \pi\left(\dfrac{xr}{h}\right)^2 dx \\[5pt] &=& \pi \frac{r^2}{h^2} \int_0^h x^2 dx \\[5pt] &=& \pi \frac{r^2}{h^2} \left[x^2\right]_0^h \\[5pt] &=& \pi \frac{r^2}{h^2} \cdot \frac{h^3}{3} \\[5pt] &=& \frac{1}{3}\pi r^2 h \\[5pt] \end{eqnarray}と求めることができます。 $\dfrac{1}{3}$ は、たどっていくと、 $x^2$ を積分したときに出てきたものだったんですね。

一般の場合

一般の場合もほとんど同じ流れです。ある立体を、$x$ 軸に垂直な平面で切ったときの断面の面積を $S(x)$ とします。$V(x)$ がこの立体の体積を表す関数だとして、これを求めてみます。

$x=c$ と $x=c+\Delta x$ という2つの平面で立体を切ります。この区間での $S(x)$ の最小値を $m$ とし、最大値を $M$ とすると、\[ m\Delta x \leqq V(c+\Delta x)+V(c)\leqq M\Delta x \]となります。 $\Delta x$ で割り、 $\Delta x\to 0$ とすると、 $m$ も $M$ も $S(c)$ に近づいていくので、\[ V'(c)=S(c) \]となります。これがすべての $c$ についてなりたつことから、$V(x)$ を微分すれば $S(x)$ になることがわかります。逆にいうと、$S(x)$ を積分をすれば $V(x)$ が求められる、ということです。よって、この立体で $x=a$ と $x=b$ の間（$a\lt b$）にある、この立体の体積は\[ \int_a^b S(x) dx \]で求めることができます。

先ほどは円すいの場合を見ましたが、角すいの場合も同じです。

底面積が $S$ で高さが $h$ の角すいがあったとしましょう。高さが $x$ のところで切ったときの断面積を $S'$ とすると、断面と底面は相似で、相似比は $x:h$ なので、\[ S':S=x^2:h^2 \]が成り立つので、\[ S'=\frac{x^2}{h^2}S \]となります。よって、体積を求めるにはこれを積分して
\begin{eqnarray} & & \int_0^h \frac{x^2}{h^2}S dx \\[5pt] &=& \frac{S}{h^2} \int_0^h x^2 dx \\[5pt] &=& \frac{S}{h^2} \left[\frac{1}{3}x^3\right]_0^h \\[5pt] &=& \frac{S}{h^2} \cdot \frac{h^3}{3} \\[5pt] &=& \frac{Sh}{3} \\[5pt] \end{eqnarray}と求められます。角すいの場合にも $\dfrac{1}{3}$ は $x^2$ の積分によって出てくることがわかります。

おわりに

ここでは、積分を使って体積を求める方法を見てきました。断面積を積分することで体積を求めることができます。