【基本】ベクトルの足し算

🕒 2017/08/02 🔄 2024/07/06

ここでは、ベクトルの足し算について見ていきます。

📘 目次

ベクトルの足し算について考える

ベクトルというのは、向きと大きさを持つものでしたね（参考：【基本】ベクトル）。「向き」があるので、単純に「足す」といってもどう決めるのがいいか、あまり明らかではありません。

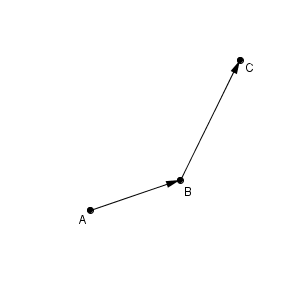
ただ、上のような場合に、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ BC } }$ という2つのベクトルを足す場合はどうでしょうか。この2つのベクトルを足すなら、なんとなく次のように決めるのが自然な気がしてきませんか？

これを式で表すと、\[ \overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BC } }=\overrightarrow{ \mathrm{ AC } } \]となります。これがベクトルの足し算の基本的な考え方です。 AB, BC というように、しりとりのように足せば、間を取り除いて AC という結論になるので、見た目としてもわかりやすいですね。

また、次の図からも、このような決め方が自然だと感じられると思います。

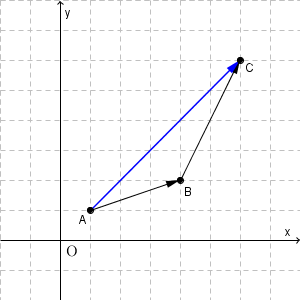
座標上で考えてみました。 $\overrightarrow{ \mathrm{ AB } }$ の向きと大きさは、横に3つ分・上に1つ分で表すことができます。 $\overrightarrow{ \mathrm{ BC } }$ は、横に2つ分・上に4つ分です。これらの和は、横に5つ分・上に5つ分となりますが、これは $\overrightarrow{ \mathrm{ AC } }$ の向き・大きさと一致しています。

そのため、しりとりのようにして足し算を定めれば、向きと大きさ、両方が足されている、と考えることができますね。

ベクトルの足し算についてもっと考える

ベクトルの足し算について考えましたが、先ほどの例では、しりとりのようになっていましたね。しかし、しりとりになっている場合しかダメ、というのは不便です。

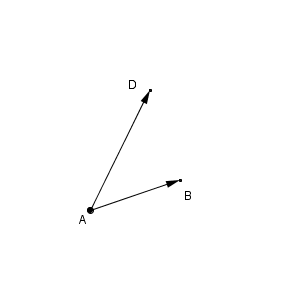
図のような状況で、\[ \overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ AD } } \]を考えるにはどうすればいいでしょうか。ここで思い出したいのが、【基本】ベクトルで見た、「ベクトルが等しいとは」についてです。2つのベクトルの向きと大きさがそれぞれが同じであれば、それらのベクトルは同じとみなすのでしたね。

なので、 $\overrightarrow{ \mathrm{ AD } }$ と同じ向き・同じ大きさの別のベクトルを考えることにしましょう。

上のように、 B を出発して、 A から D の向きに、 AD の長さだけ移動した C をとります。そうすれば、 $\overrightarrow{ \mathrm{ AD } }=\overrightarrow{ \mathrm{ BC } }$ となります。 $\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BC } }$ なら、先ほどと同じように $\overrightarrow{ \mathrm{ AC } }$ と計算することができますね。

この決め方からもわかる通り、四角形 ABCD は平行四辺形になります。よって、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ AD } }$ を足す場合は、この2つを元に平行四辺形を作れば、その対角線が、足した後のベクトルになるわけですね。

2つのベクトルが離れている場合は、平行移動をして1つ目のようにしりとりのようにするか、2つ目のように平行四辺形の対角線のようにしてから、足すようにします。どちらの方法でも、同じベクトルが得られます。

交換法則と結合法則

先ほど見た通り、平行四辺形の対角線の考え方で見ると、足す順番を変えても結果が変わらないことがわかります。

この性質は交換法則といい、式で表すと次のようになります。\[ \vec{a}+\vec{b}=\vec{b}+\vec{a} \]

また、次の図から、 $\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BC } }+\overrightarrow{ \mathrm{ CD } }$ の、どこから足すかを変えても結果が変わらないこともわかるでしょう。

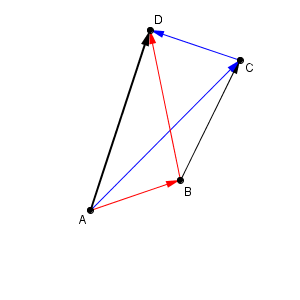
左側を先に足したものが青、右側を先に足したものが赤ですが、最終的にどちらも太線の $\overrightarrow{ \mathrm{ AD } }$ となります

この性質は結合法則と言い、式で表すと次のようになります。\[ (\vec{a} +\vec{b}) +\vec{c} = \vec{a} +(\vec{b} +\vec{c}) \]

普通の足し算では当然成り立つ性質ですが、ベクトルでも同じように成り立ちます。名前を覚える必要はありませんが、このような性質を持っていることは覚えておきましょう。

ベクトルの足し算の例

それでは、具体的な例を使って、ベクトルの足し算を見てみましょう。

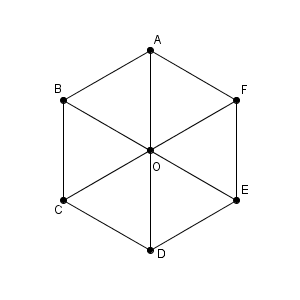
この六角形 ABCDEF は、正六角形です。これをもとに考えてみます。

まず、 $\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BC } }$ は $\overrightarrow{ \mathrm{ AC } }$ となります。

$\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ AF } }$ は、平行四辺形 ABOF に着目すれば $\overrightarrow{ \mathrm{ AO } }$ であることがわかります。

$\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ CD } }$ であれば、 $\overrightarrow{ \mathrm{ CD } }=\overrightarrow{ \mathrm{ BO } }$ であることから、 $\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BO } }$ を考えればいいので、 $\overrightarrow{ \mathrm{ AO } }$ となります。計算しやすいように平行移動をして、しりとりを作り出しています。

このように、平行移動をして計算しやすいベクトルに置き換え、しりとりのようにするか、平行四辺形を作って、足した後のベクトルを求めるようにします。