【基本】2つの円と共通接線

ここでは、2つの円の位置関係や、共通接線について見ていきます。

2つの円の位置関係

【基本】円の接線では、円と直線の位置関係を見ましたが、ここでは、2つの円の位置関係を見ていきます。

円と直線の位置関係では、共有点が1点だけの「接する」ときが一番特徴的でした。2つの円についても、共有点が1点だけの場合があります。図をかいてみましょう。

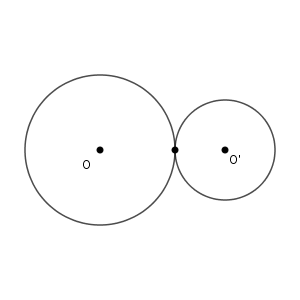
このようになっている場合です。ただ、2つの円の場合は、共有点が1点となるケースはもう1つあります。次のような場合です。

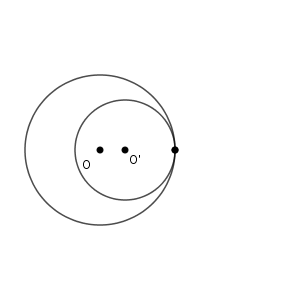
片方の円がもう片方の円の内側にある場合ですね。どちらのケースも「2つの円は接する」といいますが、区別できた方がいいので、それぞれに名前がついています。1つ目のケースを外接、2つ目のケースを内接といいます。

1つ目のケースよりも2つの円が遠ざかると、共有点はなくなります。

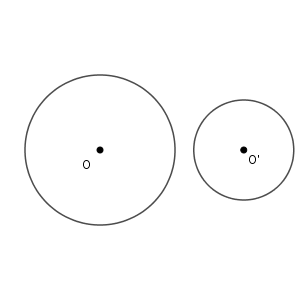
外接と内接の間の場合には、共有点は2点となります。

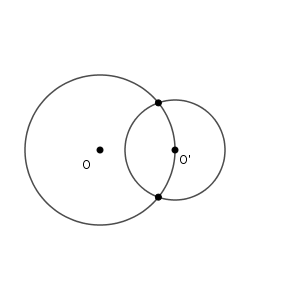
また、内接のときよりも、内側の円がさらに内側に入ると、共有点はなくなります。

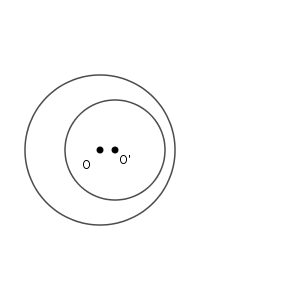
つまり、2つの円がどれだけ近いか遠いかによって、共有点の個数は、0⇒1⇒2⇒1⇒0 と変化していくことがわかります。

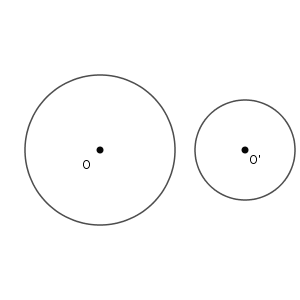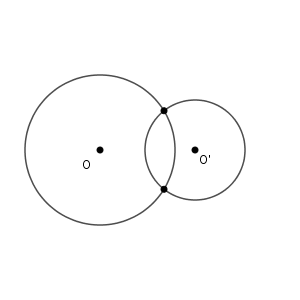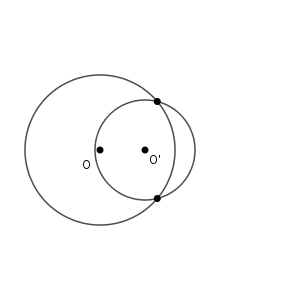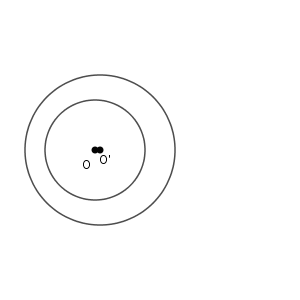
月食や日食のような動きですね。

それぞれのケースを、数式で表してみます。2つの円の半径を $r_1,r_2$ とします。また、2つの円がどれだけ離れてるかを表すものとして、円の中心間の距離を $d$ とすることにします。

2つの円が互いに外部にあって離れているケースは\[ d\gt r_1+r_2 \]と書けます。外接しているケースは、\[ d=r_1+r_2 \]となります。また、内接しているケースは、半径の差と中心間の距離が一致しているときです。

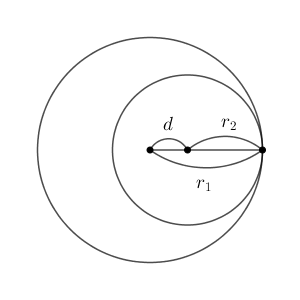
つまり、\[ d=|r_1-r_2| \]のときです。中心間の距離がこれより大きいと2点で交わるので、2点で交わるケースは\[ |r_1-r_2|\lt d \lt r_1+r_2 \]です。また、片方が他方の内部にあるのは\[ d\lt|r_1-r_2| \]のとき、となります。

共通接線

上で見たように、2つの円の位置関係は、共有点の個数に着目すると、中心間の距離に応じて 0⇒1⇒2⇒1⇒0 と変化していくのでした。ただ、0のケースと1のケースがダブっていますね。これを区別する方法はないでしょうか。

そこで使えるのが、共通接線です。2つの円のどちらにも接する直線のことです。

例えば、内接する場合は、次のように、共通接線は1本だけ引くことができます。2つの円の接点を通る直線です。

一方、外接する場合は、同じように2つの円の接点を通る接線が引けますが、他にも2本の共通接線が引けます。

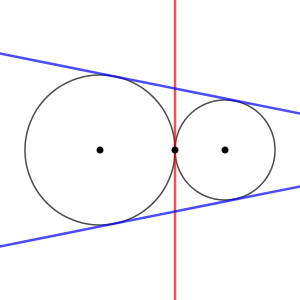
赤の直線も青の直線も、どちらも共通接線です。外接する場合は、合計3本引けるということですね。

内接する場合が1本、外接する場合が3本なので、2つの円が2点で交わる場合は、2本引けるのではないかと予想できますが、実際に2本引けます。

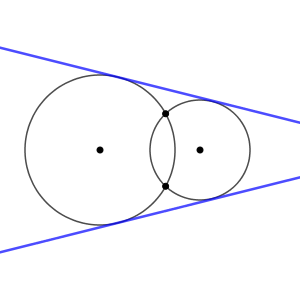
この流れで行くと、2つの円が互いに外部あるケースは4本引けると予想できます。次のようになります。

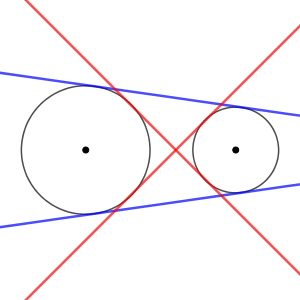
青い2本はすぐに思いつきますが、赤い2本は少し思いつきにくいかもしれません。

共通接線のうち、接線に関して2つの円が同じ側にあるようなものを共通外接線といい、反対側にあるようなものを共通内接線といいます。共通内接線は、円の中心間を結んだ線分と交わる接線、ともいえます。ここまでの図で、青い接線が共通外接線、赤い接線が共通内接線を表しています。

片方が他方の内側にある場合は、共通接線は引けません。

ここまでの内容をまとめておきます。

なお、2つの円の半径が同じ場合でも、外部ある場合、外接する場合、2点で交わる場合は同じです。これら3つ以外の場合は $d=0$ のときであり、2円が重なる場合です。内接することや片方が他方の内部にあることはありません。

おわりに

ここでは、2つの円の位置関係を見てきました。半径と中心間の距離、共通接線の本数で特徴づけることができました。

共通内接線は見落としがちなので注意しましょう。また、「接する」と聞いて「外接する」と思い込んでしまうこともよくある間違いなので注意しましょう。