東京大学理系 2024年度第4問解説

🕒 2024/02/25 🔄 2024/03/02

問題編

問題

　$f(x)=-\dfrac{\sqrt{2}}{4}x^2+4\sqrt{2}$ とおく。 $0\lt t\lt 4$ を満たす実数 $t$ に対し、座標平面上の点 $(t,f(t))$ を通り、この点において放物線 $y=f(x)$ と共通の接線を持ち、 $x$ 軸上に中心を持つ円を $C_t$ とする。

(1) 円 $C_t$ の中心の座標を $(c(t),0)$, 半径を $r(t)$ とおく。 $c(t)$ と $\{r(t)\}^2$ を $t$ の整式で表せ。

(2) 実数 $a$ は $0\lt a\lt f(3)$ を満たすとする。円 $C_t$ が点 $(3,a)$ を通るような実数 $t$ は $0\lt t\lt 4$ の範囲にいくつあるか。

考え方

何をすればいいかは難しくないですが、計算が面倒です。特に、「これを微分するのか。。。」という気持ちになりますが、微分した結果はスッキリした形になります。

解答編

問題

　$f(x)=-\dfrac{\sqrt{2}}{4}x^2+4\sqrt{2}$ とおく。 $0\lt t\lt 4$ を満たす実数 $t$ に対し、座標平面上の点 $(t,f(t))$ を通り、この点において放物線 $y=f(x)$ と共通の接線を持ち、 $x$ 軸上に中心を持つ円を $C_t$ とする。

(1) 円 $C_t$ の中心の座標を $(c(t),0)$, 半径を $r(t)$ とおく。 $c(t)$ と $\{r(t)\}^2$ を $t$ の整式で表せ。

解答

(1)
\[ f'(x)=-\frac{\sqrt{2}}{2}x \]なので、点 $(t,f(t))$ における $y=f(x)$ の接線の傾きは $-\dfrac{\sqrt{2}t}{2}$ である。よって、法線の傾きは $\dfrac{\sqrt{2}}{t}$ となる。この法線は必ず $x$ 軸と交わるから、その交点を中心とし、点 $(t,f(t))$ を通る円をかけば、それが $C_t$ と一致する。

法線の方程式は\[ y-f(t)=\frac{\sqrt{2}}{t}(x-t) \]なので、
\begin{eqnarray} 0-f(t) &=& \frac{\sqrt{2}}{t}(c(t)-t) \\[5pt] \frac{\sqrt{2}}{4}t^2-4\sqrt{2} &=& \frac{\sqrt{2}}{t}(c(t)-t) \\[5pt] \frac{1}{4}t^2-4 &=& \frac{1}{t}(c(t)-t) \\[5pt] \frac{1}{4}t^3-4t &=& c(t)-t \\[5pt] c(t) &=& \frac{1}{4}t^3-3t \end{eqnarray}となる。

また、 $\{r(t)\}^2$ は、円の中心と $(t,f(t))$ との距離の2乗なので
\begin{eqnarray} \{r(t)\}^2 &=& \{c(t)-t\}^2 +\{f(t)\}^2 \\[5pt] &=& \left(\frac{1}{4}t^3-3t-t\right)^2+\left(-\dfrac{\sqrt{2}}{4}t^2+4\sqrt{2}\right)^2 \\[5pt] &=& t^2\left(\frac{1}{4}t^2-4\right)^2+2\left(\dfrac{1}{4}t^2-4\right)^2 \\[5pt] &=& (t^2+2)\left(\frac{t^2-16}{4}\right)^2 \\[5pt] &=& \frac{1}{16}(t^2+2)(t+4)^2(t-4)^2 \\[5pt] \end{eqnarray}となる。

よって、

　$c(t)=\dfrac{1}{4}t^3-3t$

　$\{r(t)\}^2=\dfrac{1}{16}(t^2+2)(t+4)^2(t-4)^2$

となる。（答）

解答編　つづき

問題

(2) 実数 $a$ は $0\lt a\lt f(3)$ を満たすとする。円 $C_t$ が点 $(3,a)$ を通るような実数 $t$ は $0\lt t\lt 4$ の範囲にいくつあるか。

解答

(2)
円 $C_t$ が $(3,a)$ を通ることは\[ (3-c(t))^2+a^2=\{r(t)\}^2 \]を満たすことと同値である。以下では\[ g(t)=\{r(t)\}^2-(3-c(t))^2 \]とおいて、 $g(t)$ のとる値について考える。

\begin{eqnarray} g(t) &=& \dfrac{1}{16}(t^2+2)(t+4)^2(t-4)^2 -(c(t)-3)^2 \\[5pt] &=& \dfrac{1}{16}(t^2+2)(t^2-16)^2 -\left(\dfrac{1}{4}t^3-3t-3\right)^2 \\[5pt] \end{eqnarray}なので \begin{eqnarray} g'(t) &=& \dfrac{1}{16}\{ 2t(t^2-16)^2+(t^2+2)\cdot2(t^2-16)\cdot 2t \} \\ & & -2\left(\dfrac{1}{4}t^3-3t-3\right)\left(\dfrac{3}{4}t^2-3\right) \\[5pt] &=& \dfrac{2t(t^2-16)}{16}\{ (t^2-16)+2(t^2+2) \} \\ & & -2\cdot\frac{1}{4}(t^3-12t-12)\cdot\frac{1}{4}(3t^2-12) \\[5pt] &=& \dfrac{t(t^2-16)}{8}(3t^2-12) \\ & & -\frac{1}{8}(t^3-12t-12)(3t^2-12) \\[5pt] &=& \frac{3t^2-12}{8}\{t(t^2-16)-(t^3-12t-12)\} \\[5pt] &=& \frac{3t^2-12}{8}(-4t+12) \\[5pt] &=& -\frac{3}{2}(t+2)(t-2)(t-3) \\[5pt] \end{eqnarray}となる。よって、 $0\lt t\lt 4$ の範囲で増減表をかくと次のようになる。 \begin{array}{c|ccccc} t & 0 & \cdots & 2 & \cdots & 3 & \cdots & 4 \\ \hline g'(t) & & - & 0 & + & 0 & - & \\ \hline g(t) & & \searrow & & \nearrow & & \searrow & & \end{array}

ここで、\[ g(t)=\dfrac{1}{16}(t^2+2)(t^2-16)^2 -\left(\dfrac{1}{4}t^3-3t-3\right)^2 \]より
\begin{eqnarray} g(0) &=& \frac{2\cdot 16^2}{16}-\left(\dfrac{0^3}{4}-3\cdot 0-3\right)^2 = 32-9=23 \\[5pt] g(2) &=& \frac{6\cdot 12^2}{16}-\left(\dfrac{2^3}{4}-3\cdot 2-3\right)^2 = 54-49=5 \\[5pt] g(3) &=& \frac{11\cdot 7^2}{16}-\left(\dfrac{3^3}{4}-3\cdot 3-3\right)^2 = \frac{539-441}{16}=\frac{49}{8} \\[5pt] g(4) &=& \frac{18\cdot 0^2}{16}-\left(\dfrac{4^3}{4}-3\cdot 4-3\right)^2 = -1 \\[5pt] \end{eqnarray}なので、 $y=g(t)$ $(0\lt t\lt 4)$ のグラフは次のようになる。

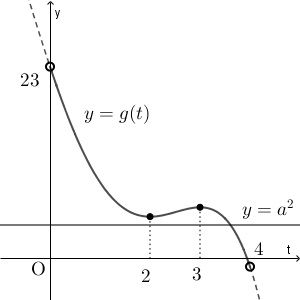
円 $C_t$ が点 $(3,a)$ を通るような実数 $t$ の個数は、 $y=g(t)$ と $y=a^2$ の共有点の個数と一致する。
\begin{eqnarray} f(3)=\frac{7\sqrt{2}}{4}=\sqrt{g(3)} \end{eqnarray}より、 $a^2$ は $0$ から $g(3)$ の値までを動くので、

・$0\lt a\lt \sqrt{5}$ のときは1個

・$a=\sqrt{5}$ のときは2個

・$\sqrt{5}\lt a \lt\dfrac{7\sqrt{2}}{4}$ のときは3個

となる。（答）