東京大学文系 2025年度第4問解説

🕒 2025/03/01

問題編

問題

　$a$ を実数とする。座標平面において、次の連立不等式の表す領域の面積を $S(a)$ とする。
\begin{eqnarray} \left\{ \begin{array}{l} y \leqq -\dfrac{1}{2}x^2+2 \\[5pt] y \geqq |x^2+a| \\[5pt] -1 \leqq x\leqq 1 \end{array} \right. \end{eqnarray} $a$ が $-2\leqq a\lt 2$ の範囲を動くとき、 $S(a)$ の最大値を求めよ。

考え方

$a$ の値によって $y=|x^2+a|$ の形が変わるので、場合分けが必要です。求めたいのは面積ではなく、面積の最大値だけなので、求めなくてもいいものは極力求めないようにしましょう。ただ、省力化しても、計算は大変です。

解答編

問題

　$a$ を実数とする。座標平面において、次の連立不等式の表す領域の面積を $S(a)$ とする。
\begin{eqnarray} \left\{ \begin{array}{l} y \leqq -\dfrac{1}{2}x^2+2 \\[5pt] y \geqq |x^2+a| \\[5pt] -1 \leqq x\leqq 1 \end{array} \right. \end{eqnarray} $a$ が $-2\leqq a\lt 2$ の範囲を動くとき、 $S(a)$ の最大値を求めよ。

解答

$a\lt 0$ のとき、 $y=|x^2+a|$ と $x$ 軸との交点の座標は $(\sqrt{-a},0)$, $(-\sqrt{-a},0)$ である。この交点が $-1\leqq x\leqq 1$ の間にあるのは、 $a\geqq -1$ のときである。

(i) $-2 \leqq a \lt -1$ のとき

このとき、 $y=|x^2+a|$ と $x$ 軸との交点は、 $-1\leqq x\leqq 1$ の範囲外にあるので、領域は以下のようになる。

$-1\leqq x\leqq 1$ の範囲の、 $y=|x^2+a|=-x^2-a$ のグラフは、 $a$ が大きくなるほど下に移動するので、この範囲では $S(a)$ は単調増加である。

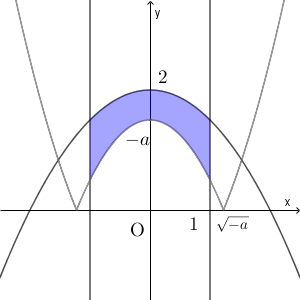
(ii) $-1 \leqq a \lt 0$ のとき

このとき、 $y=|x^2+a|$ と $x$ 軸との交点は、 $-1\leqq x\leqq 1$ の範囲内にあるので、領域は以下のようになる。

これより、 $S(a)$ は、

　$x=1$, $x=-1$, $y=-\dfrac{1}{2}x^2+2$ と $x$ 軸で囲まれた部分の面積 $A$

から、

　$y=-x^2-a$ と $x$ 軸で囲まれた部分の面積 $B$

と

　$y=x^2+a$, $x=1$ と $x$ 軸で囲まれた部分の面積を2倍したもの $C$

を引けば求められる。
\begin{eqnarray} A &=& 2 \int_0^1 \left(-\dfrac{x^2}{2}+2\right)dx \\[5pt] &=& 2 \left[ -\frac{x^3}{6}+2x \right]_0^1 \\[5pt] &=& 2 \left( -\frac{1}{6}+2 \right) \\[5pt] &=& \frac{11}{3} \\[5pt] \end{eqnarray} \begin{eqnarray} B &=& 2 \int_0^{\sqrt{-a}} \left(-x^2-a\right)dx \\[5pt] &=& 2 \left[ -\frac{x^3}{3}-ax \right]_0^{\sqrt{-a}} \\[5pt] &=& 2 \left( -\frac{-a\sqrt{-a}}{3}-a\sqrt{-a} \right) \\[5pt] &=& -\frac{4a\sqrt{-a}}{3} \\[5pt] \end{eqnarray} \begin{eqnarray} C &=& 2 \int_{\sqrt{-a}}^1 \left(x^2+a\right)dx \\[5pt] &=& 2 \left[ \frac{x^3}{3}+ax \right]_{\sqrt{-a}}^1 \\[5pt] &=& 2 \left( \frac{1}{3}+a -\frac{-a\sqrt{-a}}{3}-a\sqrt{-a} \right) \\[5pt] &=& \frac{2}{3}+2a-\frac{4a\sqrt{-a}}{3} \end{eqnarray}となるから \begin{eqnarray} S(a) &=& A-B-C \\[5pt] &=& \frac{11}{3} +\frac{4a\sqrt{-a}}{3} -\left( \frac{2}{3}+2a-\frac{4a\sqrt{-a}}{3} \right) \\[5pt] &=& 3-2a +\frac{8a\sqrt{-a}}{3} \end{eqnarray}となる。

ここで、 $t=\sqrt{-a}$ とおくと、 $0\lt t\leqq 1$ であり、 $-a=t^2$ なので $S(a)$ を $t$ で表すと
\begin{eqnarray} & & 3+2t^2 +\frac{8(-t^2)t}{3} \\[5pt] &=& -\frac{8}{3}t^3+2t^2+3 \end{eqnarray}と表すことができる。これを $f(t)$ とおくと \begin{eqnarray} f'(t) &=& -8t^2+4t=4t(-2t+1) \end{eqnarray}なので、増減表は以下のようになる。 \begin{array}{c|ccccc} x & 0 & \cdots & \frac{1}{2} & \cdots & 1 \\ \hline f'(x) & & + & 0 & - & \\ \hline f(x) & & \nearrow & & \searrow & & \end{array}ここで \begin{eqnarray} f\left(\frac{1}{2}\right) &=& -\frac{8}{3}\cdot\frac{1}{8}+2\cdot\frac{1}{4}+3 \\[5pt] &=& -\frac{1}{3}+\frac{1}{2}+3 \\[5pt] &=& \frac{19}{6} \end{eqnarray}なので、 $f(t)$ は $t=\dfrac{1}{2}$ のときに最大値 $\dfrac{19}{6}$ をとることがわかる。今考えている範囲での $S(a)$ の最大値も $\dfrac{19}{6}$ だとわかり、この値をとるのは $a=-\dfrac{1}{4}$ のときである。

(iii) $0\leqq a\lt 2$ のとき

$y=|x^2+a|=x^2+a$ なので、領域は以下のようになる。