東京大学 文系 2025年度 第2問 解説
問題編
問題
平面上で $\mathrm{AB} = \mathrm{AC} = 1$ である二等辺三角形 $\mathrm{ABC}$ を考える。正の実数 $r$ に対し、$\mathrm{A,B,C}$ それぞれを中心とする半径 $r$ の円3つを合わせた領域を $D_r$ とする。ただし、この問いでは、三角形と円は周とその内部からなるものとする。辺 $\mathrm{AB,AC,BC}$ がすべて $D_r$ に含まれるような最小の $r$ を $s$、三角形 $\mathrm{ABC}$ が $D_r$ に含まれるような最小の $r$ を $t$ と表す。
(1) $\angle\mathrm{BAC}=\dfrac{\pi}{3}$ のとき、 $s$ と $t$ を求めよ。
(2) $\angle\mathrm{BAC}=\dfrac{2\pi}{3}$ のとき、 $s$ と $t$ を求めよ。
(3) $0\lt\theta\lt \pi $ を満たす $\theta$ に対して、 $\angle\mathrm{BAC}=\theta$ のとき、 $s$ と $t$ を $\theta$ を用いて表せ。
考え方
(1)と(2)は角や辺を具体的に求められるので考えやすいです。これらを使って、どういうときに最小になるかを考えます。そうすると、どこかを境い目にして場合分けをしないといけないことがわかります。
どこまで丁寧に書くかが悩ましいところですが、試験中であれば、図をかいてある程度説明を簡略化するしかないと思います。
解答編
問題
平面上で $\mathrm{AB} = \mathrm{AC} = 1$ である二等辺三角形 $\mathrm{ABC}$ を考える。正の実数 $r$ に対し、$\mathrm{A,B,C}$ それぞれを中心とする半径 $r$ の円3つを合わせた領域を $D_r$ とする。ただし、この問いでは、三角形と円は周とその内部からなるものとする。辺 $\mathrm{AB,AC,BC}$ がすべて $D_r$ に含まれるような最小の $r$ を $s$、三角形 $\mathrm{ABC}$ が $D_r$ に含まれるような最小の $r$ を $t$ と表す。
(1) $\angle\mathrm{BAC}=\dfrac{\pi}{3}$ のとき、 $s$ と $t$ を求めよ。
解答
一般的に、 $\angle\mathrm{R}=90^{\circ}$ の直角三角形 $\mathrm{PQR}$ について、半径が $\mathrm{PQ}$ と同じ長さで中心が $\mathrm{P}$ の円は三角形 $\mathrm{PQR}$ を含む。このことを (*) で表すことにする。
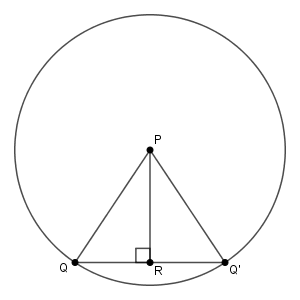
これは、$\mathrm{PR}$ を中心として $\mathrm{Q}$ を対称移動した点を $\mathrm{Q'}$ としたときに、おうぎ形 $\mathrm{PQQ'}$ が三角形 $\mathrm{PQQ'}$ を含むことからわかる。
以下では、辺 $\mathrm{AB}$ の中点を $\mathrm{D}$ とし、辺 $\mathrm{AB}$ の垂直二等分線と直線 $\mathrm{BC}$ との交点を $\mathrm{E}$ とする。また、辺 $\mathrm{BC}$ の中点を $\mathrm{M}$ とする。
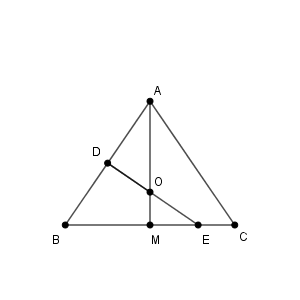
直線 $\mathrm{AM}$ は辺 $\mathrm{BC}$ の垂直二等分線なので、 $\mathrm{AM}$ と $\mathrm{DE}$ の交点は、三角形 $\mathrm{ABC}$ の外接円の中心である。これを点 $\mathrm{O}$ とする。
(1)
$\angle\mathrm{BAC}=\dfrac{\pi}{3}$ のとき、三角形 $\mathrm{ABC}$ は1辺が $1$ の正三角形である。
$r\lt\dfrac{1}{2}$ のときは $D_r$ は $\mathrm{D}$ を含まない。一方、 $r=\dfrac{1}{2}$ のときはすべての辺が $D_r$ に含まれる。よって、 $s=\dfrac{1}{2}$ である。
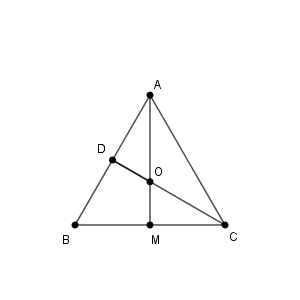
三角形 $\mathrm{ABC}$ の外心 $\mathrm{O}$ は三角形 $\mathrm{ABC}$ 内の点であり、外接円の半径は $\dfrac{\sqrt{3}}{3}$ なので、 $r\lt\dfrac{\sqrt{3}}{3}$ のときは $D_r$ は $\mathrm{O}$ を含まない。
一方、 $r=\dfrac{\sqrt{3}}{3}$ のとき、(*) より、三角形 $\mathrm{ADO}$ 内の点はすべて $D_r$ に含まれる。同様に、三角形 $\mathrm{ABC}$ を、辺の中点と外心を結ぶ線で分割して考えれば、すべての点が $D_r$ に含まれることがわかる。よって、 $t=\dfrac{\sqrt{3}}{3}$ である。
以上から、 $s=\dfrac{1}{2}$, $t=\dfrac{\sqrt{3}}{3}$ …(答)
解答編 つづき
問題
(2) $\angle\mathrm{BAC}=\dfrac{2\pi}{3}$ のとき、 $s$ と $t$ を求めよ。
解答
(2)
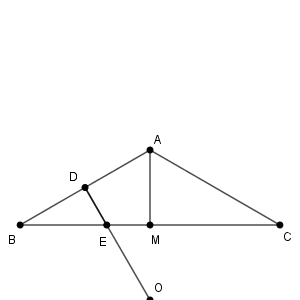
このとき、 $\mathrm{BD}=\dfrac{1}{2}$ で、\[ \mathrm{BE}=\mathrm{BD}\cdot \dfrac{2}{\sqrt{3}}=\frac{\sqrt{3}}{3} \]である。
$r\lt\dfrac{\sqrt{3}}{3}$ のとき、 $D_r$ は $\mathrm{E}$ を含まない。
一方、 $r=\dfrac{\sqrt{3}}{3}$ のとき、 まず、 $\mathrm{BE\gt BD}$ より、辺 $\mathrm{AB,AC}$ はすべて $D_r$ に含まれる。線分 $\mathrm{BE}$ は $\mathrm{B}$ を中心とする円に含まれる。$\mathrm{AE=BE}$ より、(*) から、線分 $\mathrm{EM}$ は $\mathrm{A}$ を中心とする円に含まれる。対称性より、すべての辺が $D_r$ に含まれることがわかる。よって、 $s=\dfrac{\sqrt{3}}{3}$ である。
また、このとき、(*) より、 $D_r$ は、$\triangle\mathrm{BDE}$, $\triangle\mathrm{ADE}$, $\triangle\mathrm{AEM}$ も含むので、 $t=\dfrac{\sqrt{3}}{3}$ であることもわかる。
よって、 $s=t=\dfrac{\sqrt{3}}{3}$ …(答)
解答編 つづき
問題
(3) $0\lt\theta\lt \pi $ を満たす $\theta$ に対して、 $\angle\mathrm{BAC}=\theta$ のとき、 $s$ と $t$ を $\theta$ を用いて表せ。
解答
(3)
$\alpha=\dfrac{\theta}{2}$ とおくと、$\angle\mathrm{BAM}=\angle\mathrm{BED}=\alpha$ である。

よって、 $\mathrm{AM}=\cos\alpha$, $\mathrm{BM}=\sin\alpha$, $\mathrm{AD}=\dfrac{1}{2}$, $\mathrm{AO}=\dfrac{1}{2\cos\alpha}$, $\mathrm{BE}=\dfrac{1}{2\sin\alpha}$ となる。
(i) $0\lt \theta\leqq\dfrac{1}{3}\pi$ のとき
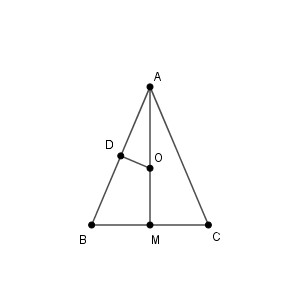
$r\lt\dfrac{1}{2}$ なら $D_r$ は $\mathrm{D}$ を含まないが、 $r=\dfrac{1}{2}$ なら $\mathrm{D}$ を含み、辺 $\mathrm{AB,AC}$ を含むことがわかる。
$0\lt\alpha\leqq\dfrac{1}{6}\pi$ より、 $\mathrm{BM}=\sin\alpha\leqq \dfrac{1}{2}$ なので、 $r=\dfrac{1}{2}$ のとき、 $D_r$ は辺 $\mathrm{BC}$ を含む。 よって、 $s=\dfrac{1}{2}$ である。
$\mathrm{AM}=\cos\alpha \geqq \dfrac{\sqrt{3}}{2}$ で、 $\mathrm{AO}=\dfrac{1}{2\cos\alpha} \leqq \dfrac{\sqrt{3}}{3}$ なので、つねに外心 $\mathrm{O}$ は三角形 $\mathrm{ABC}$ 内にある。よって、 $r\lt\mathrm{AO}$ のときは $D_r$ は $\mathrm{O}$ を含まないが、 $r=\mathrm{AO}$ のときは、 $\mathrm{\triangle ADO}$, $\mathrm{\triangle BDO}$, $\mathrm{\triangle BMO}$ を含むので、三角形 $\mathrm{ABC}$ を含む。よって、\[ t=\mathrm{AO}=\dfrac{1}{2\cos\alpha}=\dfrac{1}{2\cos\frac{\theta}{2}} \]となる。
(ii) $\dfrac{1}{3}\pi \lt \theta\leqq\dfrac{1}{2}\pi$ のとき
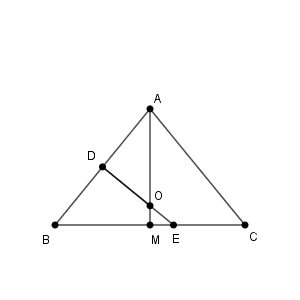
$\dfrac{1}{6}\pi\lt\alpha\leqq\dfrac{1}{4}\pi$ より、$\tan\alpha\leqq 1$ だから、 $\mathrm{BM\leqq AM}$ なので、 $r\lt\mathrm{BM}$ のとき、 $D_r$ は $\mathrm{M}$ を含まない。一方、 $r=\mathrm{BM}$ のときは、 $D_r$ は $\mathrm{M}$ を含むので、辺 $\mathrm{BC}$ を含む。
また、 $\mathrm{BM}=\sin\alpha\gt\dfrac{1}{2}$ だから、 $r=\mathrm{BM}$ のときに辺 $\mathrm{AB,AC}$ を含むこともわかる。よって、\[ s=\mathrm{BM}=\sin\alpha=\sin\frac{\theta}{2} \]である。
$\mathrm{AM}=\cos\alpha \geqq \dfrac{\sqrt{2}}{2}$ で、 $\mathrm{AO}=\dfrac{1}{2\cos\alpha} \leqq \dfrac{\sqrt{2}}{2}$ なので、つねに外心 $\mathrm{O}$ は三角形 $\mathrm{ABC}$ 内にある。よって、(i)と同様にして、 $t=\dfrac{1}{2\cos\frac{\theta}{2}}$ とわかる。
(iii) $\dfrac{1}{2}\pi\lt\theta\lt\pi$ のとき
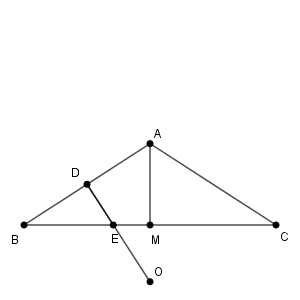
$\dfrac{1}{4}\pi\lt\alpha\lt\dfrac{1}{2}\pi$ より、 $\mathrm{AM}=\cos\alpha \lt \dfrac{\sqrt{2}}{2}$ で、 $\mathrm{AO}=\dfrac{1}{2\cos\alpha} \gt \dfrac{\sqrt{2}}{2}$ なので、つねに外心 $\mathrm{O}$ は三角形 $\mathrm{ABC}$ の外にある。また、 $\mathrm{BM}=\sin\alpha\gt \dfrac{\sqrt{2}}{2}$ と $\mathrm{BE}=\dfrac{1}{2\sin\alpha}\lt\dfrac{\sqrt{2}}{2}$ より、 $\mathrm{E}$ は線分 $\mathrm{BM}$ 上にある。
$\mathrm{AE=BE}$ より、 $r\lt\mathrm{BE}$ のとき、 $D_r$ は $\mathrm{E}$ を含まない。一方、 $r=\mathrm{BE}$ のときは、 $D_r$ は線分 $\mathrm{BE}$ を含む。また、直角三角形 $\mathrm{AEM}$ について考えると、(*) より、線分 $\mathrm{EM}$ が $D_r$ に含まれることがわかる。よって、辺 $\mathrm{BC}$ は $D_r$ に含まれる。また、 $\mathrm{BD}\lt \mathrm{BE}$ より、辺 $\mathrm{AB,AC}$ も $D_r$ に含まれる。よって、\[ s=\mathrm{BE}=\dfrac{1}{2\sin\alpha}=\dfrac{1}{2\sin\frac{\theta}{2}} \]である。
また、このとき、 $\triangle\mathrm{BDE}$, $\triangle\mathrm{ADE}$, $\triangle\mathrm{AEM}$ も $D_r$ に含まれるので、 $t=\dfrac{1}{2\sin\frac{\theta}{2}}$ もわかる。
(i)(ii)(iii) より、
(答)
$0\lt \theta\leqq\dfrac{1}{3}\pi$ のとき: $s=\dfrac{1}{2}$, $t=\dfrac{1}{2\cos\frac{\theta}{2}}$
$\dfrac{1}{3}\pi \lt \theta\leqq\dfrac{1}{2}\pi$ のとき: $s=\sin\dfrac{\theta}{2}$, $t=\dfrac{1}{2\cos\frac{\theta}{2}}$
$\dfrac{1}{2}\pi\lt\theta\lt\pi$ のとき: $s=t=\dfrac{1}{2\sin\frac{\theta}{2}}$
解説
上の解答はさすがに細かく書きすぎですが、本番では図をかいてある程度説明を省略することになると思います。
$s$ については、各辺の中点までの距離がどうなっているかを考えればよさそうだ((i)と(ii)の場合わけ)、というのは思いつきやすいですが、(2)のように、辺 $\mathrm{BC}$ 上の点の中には、 $\mathrm{B}$ より $\mathrm{A}$ のほうが近いというケースがあることに注意しましょう。
$t$ については、外心を考えればよさそうだ、というのは思いつきやすいですが、(2)のように、外心が三角形の外にある場合に注意しましょう。





