東京大学 文系 2024年度 第3問 解説
問題編
問題
座標平面上に2点 $\mathrm{O}(0,0)$, $\mathrm{A}(0,1)$ をとる。 $x$ 軸上の2点 $\mathrm{P}(p,0)$, $\mathrm{Q}(q,0)$ が、次の条件 (i), (ii) をともに満たすとする。
(i) $0\lt p\lt 1$ かつ $p\lt q$
(ii) 線分 $\mathrm{AP}$ の中点を $\mathrm{M}$ とするとき、 $\angle \mathrm{OAP}=\angle \mathrm{PMQ}$(1) $q$ を $p$ を用いて表せ。
(2) $q=\dfrac{1}{3}$ となる $p$ の値を求めよ。
(3) $\triangle\mathrm{OAP}$ の面積を $S$ 、 $\triangle\mathrm{PMQ}$ の面積を $T$ とする。 $S\gt T$ となる $p$ の範囲を求めよ。
考え方
いろいろと道具が使える分、(1)をどのように攻めていくかが難しいです。とりあえず、図形的な性質からわかることをいろいろと導いてから考えるのがいいでしょう。
(1)ができれば、(2)と(3)はただの計算問題です。(1)が一番難しいです。
解答編
問題
座標平面上に2点 $\mathrm{O}(0,0)$, $\mathrm{A}(0,1)$ をとる。 $x$ 軸上の2点 $\mathrm{P}(p,0)$, $\mathrm{Q}(q,0)$ が、次の条件 (i), (ii) をともに満たすとする。
(i) $0\lt p\lt 1$ かつ $p\lt q$
(ii) 線分 $\mathrm{AP}$ の中点を $\mathrm{M}$ とするとき、 $\angle \mathrm{OAP}=\angle \mathrm{PMQ}$(1) $q$ を $p$ を用いて表せ。
解答
(1)
$\angle \mathrm{OAP}=\theta$ とする。 $\tan\theta=p$ である。
$\mathrm{M}$ から $x$ 軸に下した垂線の足を $\mathrm{B}$ とする。
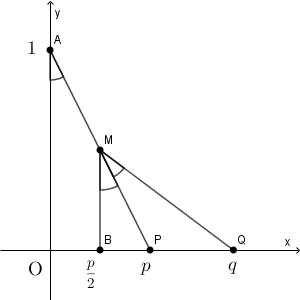
このとき、 $\mathrm{MB}$ と $\mathrm{OA}$ は平行なので、 $\angle\mathrm{BMP}=\theta$ である。直角三角形 $\mathrm{MBQ}$ について、 $\angle\mathrm{BMQ}=2\theta$ なので
\begin{eqnarray}
\mathrm{BQ}
&=&
\mathrm{MB}\cdot\tan 2\theta \\[5pt]
&=&
\frac{1}{2}\cdot\frac{2\tan\theta}{1-\tan^2\theta} \\[5pt]
&=&
\frac{p}{1-p^2} \\[5pt]
\end{eqnarray}となる。よって、
\begin{eqnarray}
q
&=&
\mathrm{OB}+\mathrm{BQ} \\[5pt]
&=&
\frac{p}{2}+\frac{p}{1-p^2} \\[5pt]
&=&
\frac{p(1-p^2)+2p}{2(1-p^2)} \\[5pt]
&=&
\frac{3p-p^3}{2(1-p^2)} \\[5pt]
&=&
\frac{p(p^2-3)}{2(p^2-1)} \\[5pt]
\end{eqnarray}なので、 $q=\dfrac{p(p^2-3)}{2(p^2-1)}$ …(答)
解答編 つづき
問題
(2) $q=\dfrac{1}{3}$ となる $p$ の値を求めよ。
解答
(2)
\begin{eqnarray}
\frac{p(p^2-3)}{2(p^2-1)} &=& \frac{1}{3} \\[5pt]
3p(p^2-3) &=& 2(p^2-1) \\[5pt]
3p^3-9p &=& 2p^2-2 \\[5pt]
3p^3-2p^2-9p+2 &=& 0 \\[5pt]
(p-2)(3p^2+4p-1) &=& 0 \\[5pt]
\end{eqnarray}と変形できる。 $3p^2+4p-1=0$ の解は
\begin{eqnarray}
p=\frac{-2\pm\sqrt{2^2+3}}{3}=\frac{-2\pm\sqrt{7}}{3}
\end{eqnarray}である。 $0\lt p\lt 1$ より、\[ p=\frac{-2+\sqrt{7}}{3} \]と求められる。(答)
解答編 つづき
問題
(3) $\triangle\mathrm{OAP}$ の面積を $S$ 、 $\triangle\mathrm{PMQ}$ の面積を $T$ とする。 $S\gt T$ となる $p$ の範囲を求めよ。
解答
(3)
$S=\dfrac{p}{2}$ である。また、 $T=\dfrac{1}{2}\cdot \dfrac{1}{2}\cdot(q-p)$ だから
\begin{eqnarray}
& & S \gt T \\[5pt]
& & \dfrac{p}{2} \gt \dfrac{1}{4}\cdot(q-p) \\[5pt]
& & 2p \gt q-p \\[5pt]
& & 3p \gt q \\[5pt]
\end{eqnarray}を解けばよい。 $p\gt 0$, $p^2-1\lt 0$ に注意して計算すると、
\begin{eqnarray}
& & 3p \gt q \\[5pt]
& & 3p \gt \frac{p(p^2-3)}{2(p^2-1)} \\[5pt]
& & 3\cdot 2(p^2-1) \lt p^2-3 \\[5pt]
& & 6p^2-6 \lt p^2-3 \\[5pt]
& & 5p^2 \lt 3 \\[5pt]
\end{eqnarray}であり、 $0\lt p\lt 1$ より、求める範囲は、\[ 0 \lt p \lt \frac{\sqrt{15}}{5} \]となる。(答)





