共通テスト 数学II・数学B・数学C 2025年度試作問題 第7問 [1] 解説
2025年度より実施される、新学習指導要領に対応した大学入試共通テストの試作問題(2022年11月発表)です。詳細はこちら。
【第4問~第7問から3問選択】
問題編
問題
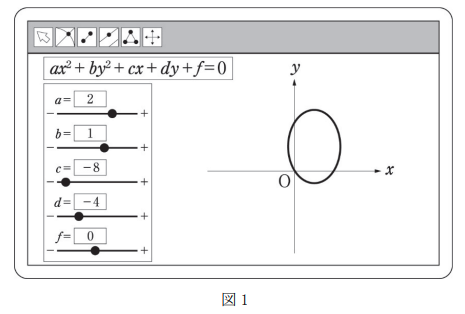
$a,b,c,d,e,f$ を実数とし、$x,y$ の方程式\[ ax^2+by^2+cx+dy+f=0 \]について、この方程式が表す座標平面上の図形をコンピュータソフトを用いて表示させる。ただし、このコンピュータソフトでは $a,b,c,d,f$ の値は十分に広い範囲で変化させられるものとする。
$a,b,c,d,f$ の値を $a=2,b=1,c=-8,d=-4,f=0$ とすると図 1 のように楕円が表示された。
方程式 $ax^2+by^2+cx+dy+f=0$ の $a,c,d,f$ の値は変えずに、$b$ の値だけを $b\geqq 0$ の範囲で変化させたとき、座標平面上には $\dBox{ア}$ 。
$\dbox{ア}$ の解答群
0: つねに楕円のみが現れ、円は現れない
1: 楕円、円が現れ、他の図形は現れない
2: 楕円、円、放物線が現れ、他の図形は現れない
3: 楕円、円、双曲線が現れ、他の図形は現れない
4: 楕円、円、双曲線、放物線が現れ、他の図形は現れない
5: 楕円、円、双曲線、放物線が現れ、また他の図形が現れることもある
考え方
新しく数学Cの分野が追加されました。平面上の曲面の分野からは、グラフツールを使った問題です。二次曲線の係数がどうなっていたらどういうグラフに対応するかがわかっていれば、難しくはないでしょう。
【第4問~第7問から3問選択】
解答編
問題
$a,b,c,d,e,f$ を実数とし、$x,y$ の方程式\[ ax^2+by^2+cx+dy+f=0 \]について、この方程式が表す座標平面上の図形をコンピュータソフトを用いて表示させる。ただし、このコンピュータソフトでは $a,b,c,d,f$ の値は十分に広い範囲で変化させられるものとする。
$a,b,c,d,f$ の値を $a=2,b=1,c=-8,d=-4,f=0$ とすると図 1 のように楕円が表示された。
方程式 $ax^2+by^2+cx+dy+f=0$ の $a,c,d,f$ の値は変えずに、$b$ の値だけを $b\geqq 0$ の範囲で変化させたとき、座標平面上には $\dBox{ア}$ 。
$\dbox{ア}$ の解答群
0: つねに楕円のみが現れ、円は現れない
1: 楕円、円が現れ、他の図形は現れない
2: 楕円、円、放物線が現れ、他の図形は現れない
3: 楕円、円、双曲線が現れ、他の図形は現れない
4: 楕円、円、双曲線、放物線が現れ、他の図形は現れない
5: 楕円、円、双曲線、放物線が現れ、また他の図形が現れることもある
解説
$a=2,c=-8,d=-4,f=0$ を代入すると
\begin{eqnarray}
2x^2+by^2-8x-4y &=& 0 \\[5pt]
\end{eqnarray}となります。 $b=2$ のときは $x^2,y^2$ の係数が等しくなるので、この場合は、円になります。具体的に計算すると
\begin{eqnarray}
2x^2+2y^2-8x-4y &=& 0 \\[5pt]
x^2+y^2-4x-2y &=& 0 \\[5pt]
(x-2)^2+(y-1)^2 &=& 5 \\[5pt]
\end{eqnarray}となることからわかります。
$b=0$ のときは、 $y=$ の式にすると $x$ の2次関数になることがわかるので、放物線となります。 $b$ が他の正の値のときは、楕円となるので、「楕円、円、放物線」が答えとなります。
双曲線が現れるのは $b$ が負の場合ですが、今のケースでは $b$ は負の値をとることはないので、双曲線は該当しません。他の図形は、例えば、 $a=b=0$ のときには、直線となるケースもありますが、これも今のケースでは起こりません。
解答
ア:2