共通テスト 数学I・数学A 2026年度 第3問 解説
【必答問題】
問題編
問題
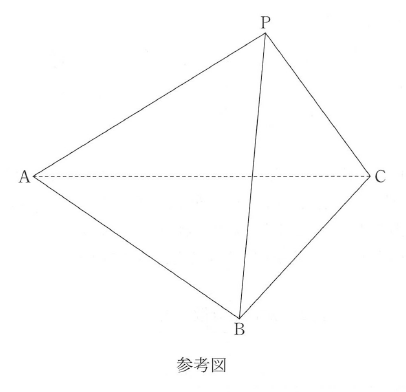
空間内に、$\mathrm{AB} = \mathrm{AC} = 10$、$\mathrm{BC} = 12$ である二等辺三角形 $\mathrm{ABC}$ がある。$\triangle \mathrm{ABC}$ の内心を $\mathrm{I}$ とし、$\triangle \mathrm{IBC}$ の重心を $\mathrm{G}$ とする。$\mathrm{G}$ を通り、$\triangle \mathrm{ABC}$ を含む平面と垂直な直線上に、$\mathrm{G}$ と異なる点 $\mathrm{P}$ がある。このとき、$\triangle \mathrm{ABC}$ を底面とする三角錐 $\mathrm{PABC}$ について考えよう。
直線 $\mathrm{AI}$ と辺 $\mathrm{BC}$ の交点を $\mathrm{D}$ とし、また、辺 $\mathrm{PA}$ 上の点 $\mathrm{E}$ は、$\angle \mathrm{PED} = \angle \mathrm{PID}$ を満たしているとする。なお、以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(1) 直線 $\mathrm{BI}$ が $\dBox{ア}$ ことに注意すると、$\triangle \mathrm{ABD}$ において線分 $\mathrm{AI}$ と $\mathrm{ID}$ の長さの比を求めることができる。よって、線分 $\mathrm{AD}$ の長さに着目すると
\[\mathrm{AI} = \myBox{イ}, \quad \mathrm{ID} = \myBox{ウ}\]であることがわかる。また、4点 $\mathrm{E}, \mathrm{I}, \mathrm{D}, \dBox{エ}$ は同一円周上にある。
よって
\[\mathrm{AE} \cdot \mathrm{AP} = \myBox{オカ}\]であることがわかる。$\dbox{ア}$ の解答群
0: 直線 $\mathrm{AC}$ と垂直に交わる
1: 直線 $\mathrm{AC}$ とねじれの位置にある
2: $\angle \mathrm{ABC}$ を2等分する
3: 辺 $\mathrm{AC}$ の中点を通る$\dbox{エ}$ の解答群
0: $\mathrm{A}$
1: $\mathrm{B}$
2: $\mathrm{C}$
3: $\mathrm{G}$
4: $\mathrm{P}$(2) 線分 $\mathrm{PI}$ と $\mathrm{DE}$ の交点を $\mathrm{F}$ とする。このとき、線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比と、三角錐 $\mathrm{PABC}$ の体積との関係について考えよう。
(i) 次の仮定1のもとで三角錐 $\mathrm{PABC}$ の体積 $V_1$ について考える。
仮定1
線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比が $\mathrm{IF} : \mathrm{FP} = 3 : 2$ である。このとき
\[\mathrm{PE} : \mathrm{EA} = \myBox{キ} : \myBox{ク}\]であるから、(1)での考察に注意すると、$\mathrm{AP} = \myBox{ケ} \sqrt{\myBox{コ}}$ となる。
したがって、直線 $\mathrm{PG}$ が $\triangle \mathrm{ABC}$ を含む平面に垂直であることに注意すると、$V_1 = \myBox{サシ}$ であることがわかる。(ii) (i)の仮定1の代わりに次の仮定2をおき、三角錐 $\mathrm{PABC}$ の体積の変化について考える。
仮定2
線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比が $\mathrm{IF} : \mathrm{FP} = 1 : 3$ である。仮定2のもとでの三角錐 $\mathrm{PABC}$ の体積 $V_2$ を、(i)で求めた $V_1$ と比較すると、$V_2$ と $V_1$ の比は
\[V_2 : V_1 = \myBox{ス} : \myBox{セ}\]であるから、$\dBox{ソ}$。$\dbox{ソ}$ の解答群
0: $V_2$ は $V_1$ より小さい
1: $V_2$ と $V_1$ は等しい
2: $V_2$ は $V_1$ より大きい
考え方
空間図形の問題ですが、平面で切って考えましょう。切り口にどの点がどのように表れるかを考えるようにしましょう。
(2)(ii)は(i)と同じような計算をしますが、いくつか固定の値はすでに求めてあるので、それを流用します。どこが固定でどこが変わる値なのか、よく状況を把握しながら計算しましょう。
【必答問題】
解答編
問題
空間内に、$\mathrm{AB} = \mathrm{AC} = 10$、$\mathrm{BC} = 12$ である二等辺三角形 $\mathrm{ABC}$ がある。$\triangle \mathrm{ABC}$ の内心を $\mathrm{I}$ とし、$\triangle \mathrm{IBC}$ の重心を $\mathrm{G}$ とする。$\mathrm{G}$ を通り、$\triangle \mathrm{ABC}$ を含む平面と垂直な直線上に、$\mathrm{G}$ と異なる点 $\mathrm{P}$ がある。このとき、$\triangle \mathrm{ABC}$ を底面とする三角錐 $\mathrm{PABC}$ について考えよう。
直線 $\mathrm{AI}$ と辺 $\mathrm{BC}$ の交点を $\mathrm{D}$ とし、また、辺 $\mathrm{PA}$ 上の点 $\mathrm{E}$ は、$\angle \mathrm{PED} = \angle \mathrm{PID}$ を満たしているとする。なお、以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(1) 直線 $\mathrm{BI}$ が $\dBox{ア}$ ことに注意すると、$\triangle \mathrm{ABD}$ において線分 $\mathrm{AI}$ と $\mathrm{ID}$ の長さの比を求めることができる。よって、線分 $\mathrm{AD}$ の長さに着目すると
\[\mathrm{AI} = \myBox{イ}, \quad \mathrm{ID} = \myBox{ウ}\]であることがわかる。また、4点 $\mathrm{E}, \mathrm{I}, \mathrm{D}, \dBox{エ}$ は同一円周上にある。
よって
\[\mathrm{AE} \cdot \mathrm{AP} = \myBox{オカ}\]であることがわかる。$\dbox{ア}$ の解答群
0: 直線 $\mathrm{AC}$ と垂直に交わる
1: 直線 $\mathrm{AC}$ とねじれの位置にある
2: $\angle \mathrm{ABC}$ を2等分する
3: 辺 $\mathrm{AC}$ の中点を通る$\dbox{エ}$ の解答群
0: $\mathrm{A}$
1: $\mathrm{B}$
2: $\mathrm{C}$
3: $\mathrm{G}$
4: $\mathrm{P}$
解説
(1)
まず、 $\mathrm{A,B,C}$ を含む平面で考えます。
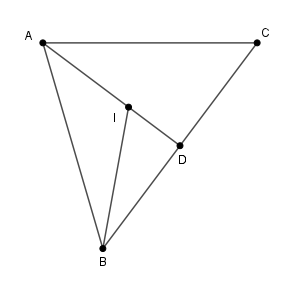
$\mathrm{I}$ は三角形 $\mathrm{ABC}$ の内心なので、直線 $\mathrm{AI}$ は $\angle \mathrm{A}$ の二等分線です。また、 $\mathrm{AB=AC}=10$ なので、三角形 $\mathrm{ABD}$ と 三角形 $\mathrm{ACD}$ は合同だとわかるから、どちらも直角三角形です。 $\mathrm{BD}=6$ だから、三平方の定理より、 $\mathrm{AD}=8$ です。
$\mathrm{I}$ は三角形 $\mathrm{ABC}$ の内心なので、直線 $\mathrm{BI}$ は $\angle \mathrm{ABC}$ の二等分線です。なので、
\begin{eqnarray}
\mathrm{AI:ID} &=& \mathrm{AB:BD} \\[5pt]
&=& 10:6 \\[5pt]
&=& 5:3 \\[5pt]
\end{eqnarray}なので、 $\mathrm{AI}=5$ と $\mathrm{ID}=3$ がわかります。
また、三角錐 $\mathrm{PABC}$ を、3点 $\mathrm{P,A,D}$ を含む平面で切ると、 $\mathrm{E}$ が $\mathrm{AP}$ 上にあることと $\mathrm{I}$ が $\mathrm{AD}$ 上にあることから、この平面には、 $\mathrm{E,I,D,P}$ があることがわかります。
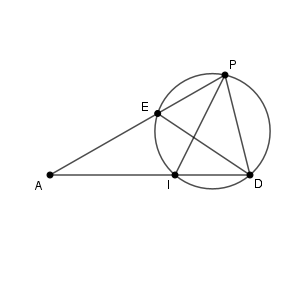
さらに、 $\mathrm{E}$ は $\angle \mathrm{PED} = \angle \mathrm{PID}$ を満たすようにとっているので、円周角の定理の逆から、 $\mathrm{E,I,D,P}$ は同一円周上にあることがわかります。
よって、方べきの定理から
\begin{eqnarray}
\mathrm{AE} \cdot \mathrm{AP}
&=&
\mathrm{AI} \cdot \mathrm{AD} \\[5pt]
&=&
5 \cdot 8 \\[5pt]
&=&
40
\end{eqnarray}と求められます。
解答
ア:2 (2点)
イウ:53 (3点)
エオカ:440 (3点)
解答編 つづき
問題
(2) 線分 $\mathrm{PI}$ と $\mathrm{DE}$ の交点を $\mathrm{F}$ とする。このとき、線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比と、三角錐 $\mathrm{PABC}$ の体積との関係について考えよう。
(i) 次の仮定1のもとで三角錐 $\mathrm{PABC}$ の体積 $V_1$ について考える。
仮定1
線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比が $\mathrm{IF} : \mathrm{FP} = 3 : 2$ である。このとき
\[\mathrm{PE} : \mathrm{EA} = \myBox{キ} : \myBox{ク}\]であるから、(1)での考察に注意すると、$\mathrm{AP} = \myBox{ケ} \sqrt{\myBox{コ}}$ となる。
したがって、直線 $\mathrm{PG}$ が $\triangle \mathrm{ABC}$ を含む平面に垂直であることに注意すると、$V_1 = \myBox{サシ}$ であることがわかる。
解説
(2)(i)
図は次のようになっています。三角錐を $\mathrm{A,P,D}$ を含む平面で切っています。
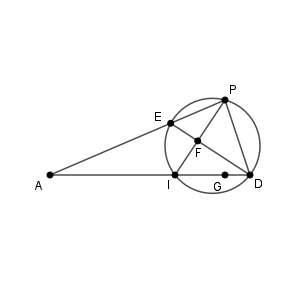
三角形 $\mathrm{API}$ と直線 $\mathrm{DE}$ について、メネラウスの定理を使うと
\begin{eqnarray}
\frac{\mathrm{PE}}{\mathrm{EA}} \cdot \frac{\mathrm{AD}}{\mathrm{DI}} \cdot \frac{\mathrm{IF}}{\mathrm{FP}} &=& 1 \\[5pt]
\frac{\mathrm{PE}}{\mathrm{EA}} \cdot \frac{8}{3} \cdot \frac{3}{2} &=& 1 \\[5pt]
\frac{\mathrm{PE}}{\mathrm{EA}} &=& \frac{1}{4} \\[5pt]
\end{eqnarray}なので、\[ \mathrm{PE} : \mathrm{EA}=1:4 \]と求められます。
(1)で、 $\mathrm{AE} \cdot \mathrm{AP}=40$ と求めていました。 $\mathrm{PE}$ を $x$ とおくと、 $\mathrm{EA}=4x$ で $\mathrm{AP}=5x$ と求められます。よって
\begin{eqnarray}
\mathrm{AE} \cdot \mathrm{AP} &=& 40 \\[5pt]
4x \cdot 5x &=& 40 \\[5pt]
x^2 &=& 2 \\[5pt]
x &=& \sqrt{2} \\[5pt]
\end{eqnarray}と求められます。なので、\[ \mathrm{AP}=5\sqrt{2} \]となります。
次に、三角錐の体積を求めます。まず、底面の三角形 $\mathrm{ABC}$ の面積は、底辺を $\mathrm{BC}$ と考えると高さが $\mathrm{AD}$ なので\[ \frac{\mathrm{BC\cdot AD}}{2}=\frac{12\cdot 8}{2}=48 \]となります。
この三角形を底面と考えると、高さは $\mathrm{GP}$ です。 $\mathrm{G}$ は三角形 $\mathrm{IBC}$ の重心で、 $\mathrm{D}$ は辺 $\mathrm{BC}$ の中点なので、 $\mathrm{IG:GD}=2:1$ です。 $\mathrm{DI}=3$ なので、 $\mathrm{IG}=2$ だから、 $\mathrm{AG}=7$ となります。よって、
\begin{eqnarray}
\mathrm{PG} &=& \sqrt{\mathrm{AP}^2-\mathrm{AG}^2} \\[5pt]
&=& \sqrt{50-49} \\[5pt]
&=& 1
\end{eqnarray}となります。
以上から三角錐の体積は
\begin{eqnarray}
\frac{1}{3} \cdot 48\cdot 1=16
\end{eqnarray}と求められます。
解答
キク:14 (3点)
ケコ:52 (3点)
サシ:16 (2点)
解答編 つづき
問題
(ii) (i)の仮定1の代わりに次の仮定2をおき、三角錐 $\mathrm{PABC}$ の体積の変化について考える。
仮定2
線分 $\mathrm{IF}$ と $\mathrm{FP}$ の長さの比が $\mathrm{IF} : \mathrm{FP} = 1 : 3$ である。仮定2のもとでの三角錐 $\mathrm{PABC}$ の体積 $V_2$ を、(i)で求めた $V_1$ と比較すると、$V_2$ と $V_1$ の比は
\[V_2 : V_1 = \myBox{ス} : \myBox{セ}\]であるから、$\dBox{ソ}$。$\dbox{ソ}$ の解答群
0: $V_2$ は $V_1$ より小さい
1: $V_2$ と $V_1$ は等しい
2: $V_2$ は $V_1$ より大きい
解説
(2)(ii)
体積の比を考える際、底面が同じなら高さの比を求めることになります。なので、先ほどと同じようにして、 $\mathrm{PG}$ を求めます。
メネラウスの定理を使うと、
\begin{eqnarray}
\frac{\mathrm{PE}}{\mathrm{EA}} \cdot \frac{\mathrm{AD}}{\mathrm{DI}} \cdot \frac{\mathrm{IF}}{\mathrm{FP}} &=& 1 \\[5pt]
\frac{\mathrm{PE}}{\mathrm{EA}} \cdot \frac{8}{3} \cdot \frac{1}{3} &=& 1 \\[5pt]
\frac{\mathrm{PE}}{\mathrm{EA}} &=& \frac{9}{8} \\[5pt]
\end{eqnarray}なので、\[ \mathrm{PE} : \mathrm{EA}=9:8 \]と求められます。
$\mathrm{PE}$ を $9x$ とおくと、 $\mathrm{EA}=8x$ で $\mathrm{AP}=17x$ と求められます。よって
\begin{eqnarray}
\mathrm{AE} \cdot \mathrm{AP} &=& 40 \\[5pt]
8x \cdot 17x &=& 40 \\[5pt]
x^2 &=& \frac{5}{17} \\[5pt]
x &=& \frac{\sqrt{85}}{17} \\[5pt]
\end{eqnarray}と求められます。なので、\[ \mathrm{AP}=\sqrt{85} \]となります。
これより
\begin{eqnarray}
\mathrm{PG} &=& \sqrt{\mathrm{AP}^2-\mathrm{AG}^2} \\[5pt]
&=& \sqrt{85-49} \\[5pt]
&=& 6
\end{eqnarray}となります。
よって、 $V_2$ と $V_1$ の比は、この高さの比を使って、 $6:1$ だとわかり、 $V_2$ の方が大きいことがわかります。
解答
スセソ:612 (4点)