共通テスト 数学I・数学A 2026年度 第2問 [2] 解説

【必答問題】

問題編

問題

　以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。

「(第1四分位数) $- 1.5 \times$ (四分位範囲)」以下の値
「(第3四分位数) $+ 1.5 \times$ (四分位範囲)」以上の値

　水泳部に所属する太郎さんは、1500 $\mathrm{m}$ 自由形におけるペース配分を考えるために、2021年に開催された東京オリンピックの男子 1500 $\mathrm{m}$ 自由形に関するデータを分析することにした。なお、自由形とは、どのような泳ぎ方で泳いでもよい競技のことである。
　分析で用いるデータは、28人の選手における、予選で計測された記録（以下、タイム）とする。ここでは、タイムは秒単位で表すものとする。例えば、15分23秒46であれば、$60 \times 15 + 23.46 = 923.46$ (秒)である。そして、公式順位（以下、順位）は、タイムの値が小さい方が上位となる。また、28人の選手それぞれのタイムについて、スタートから 750 $\mathrm{m}$ までのタイムを $T_{\text{前}}$ とし、750 $\mathrm{m}$ からゴールまでのタイムを $T_{\text{後}}$ とする。さらに、$T_{\text{前}}$ と $T_{\text{後}}$ の平均値を $T_{\text{前後}}$ とする。
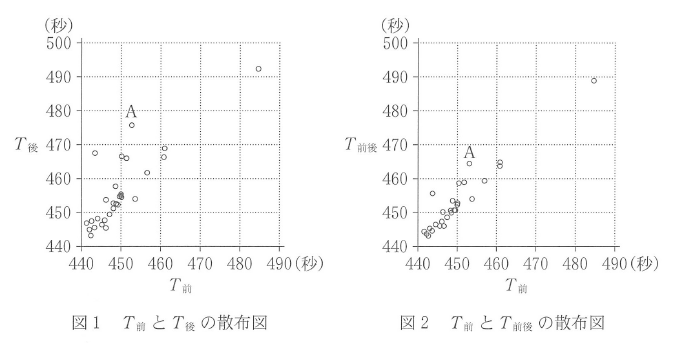
　なお、以下の図や表については、World Aquatics の Web ページをもとに作成している。

(1) 太郎さんは、$T_{\text{前}}$、$T_{\text{後}}$、$T_{\text{前後}}$ の関係を調べることにした。図1は $T_{\text{前}}$ と $T_{\text{後}}$ の散布図、図2は $T_{\text{前}}$ と $T_{\text{前後}}$ の散布図である。なお、これらの散布図には、完全に重なっている点はない。また、図1と図2において、Aを付している点は、同じ選手であることを表している。

　次の(a)、(b)は、図1と図2に関する記述である。

(a) $T_{\text{前}}$ が 470 秒未満である選手について、$T_{\text{後}}$ が 460 秒以上である選手の人数と、$T_{\text{前後}}$ が 460 秒以上である選手の人数は等しい。

(b) A を付している点が表す選手について、$T_{\text{前}}$ の値は $T_{\text{前後}}$ の値より小さく、かつ $T_{\text{後}}$ の値は $T_{\text{前後}}$ の値より大きい。

　(a)、(b)の正誤の組合せとして正しいものは $\dBox{ソ}$ である。

$\dbox{ソ}$ の解答群
　0: (a) 正 (b) 正
　1: (a) 正 (b) 誤
　2: (a) 誤 (b) 正
　3: (a) 誤 (b) 誤

(2) 太郎さんは、$T_{\text{前}}$ と $T_{\text{前後}}$ の相関係数を計算するために、表1のように、平均値、標準偏差および共分散を求めた。

表1　$T_{\text{前}}$ と $T_{\text{前後}}$ の平均値、標準偏差、共分散

	平均値	標準偏差	共分散
$T_{\text{前}}$	450	8.3	72.9
$T_{\text{前後}}$	453	9.3

　表1を用いると、$T_{\text{前}}$ と $T_{\text{前後}}$ の相関係数は $\dBox{タ}$ である。

$\dbox{タ}$ については、最も適当なものを、次の 0 ～ 9 のうちから一つ選べ。
　0: $0.01$
　1: $0.24$
　2: $0.47$
　3: $0.59$
　4: $0.72$
　5: $0.83$
　6: $0.94$
　7: $1.06$
　8: $1.38$
　9: $4.14$

(3) 太郎さんは、順位とペース配分の関係を調べるために、前半と後半という二分割だけではなく、より細かく分割されたタイムを用いて分析することにした。1500 $\mathrm{m}$ 自由形のタイムは、スタートから 50 $\mathrm{m}$ までのタイム、50 $\mathrm{m}$ から 100 $\mathrm{m}$ までのタイムのように、ゴールまで 50 $\mathrm{m}$ ごとの 30 個に分けて計測されている。そこで、これら 30 個のタイムを用いて分析する。

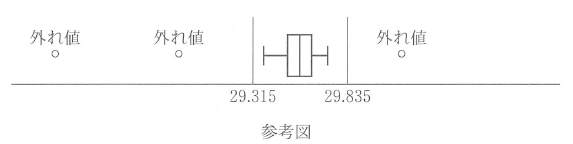
(i) 1位の選手の30個のタイムについて考えると、外れ値かどうかを判断する二つの値である $29.315$ と $29.835$ が算出され、$29.315$ 以下の2個のタイムと $29.835$ 以上の1個のタイムが外れ値と判断された。このとき、1位の選手の30個のタイムの四分位範囲は $0.\myBox{チツ}$ 秒である。

(ii) 太郎さんは28人の選手それぞれについて、30個のタイムを用いて、選手ごとの箱ひげ図を作成し、分散を計算した。図3は上から分散が小さい順になるように、28人の選手それぞれの箱ひげ図を並べたものであり、30個のタイムにおける外れ値は、白丸で示されている。なお、分散が等しい選手はいなかった。

　次の(a)、(b)は、図3に関する記述である。

(a) 28人の選手において、29秒より速いタイムはすべて外れ値である。
(b) 28人の選手から2人を選んだとき、分散の大きい選手の四分位範囲は、分散の小さい選手の四分位範囲より小さいことがある。

　(a)、(b)の正誤の組合せとして正しいものは $\dBox{テ}$ である。

$\dbox{テ}$ の解答群
　0: (a) 正 (b) 正
　1: (a) 正 (b) 誤
　2: (a) 誤 (b) 正
　3: (a) 誤 (b) 誤

(iii) 順位が1位から8位までの選手のグループを決勝進出グループ、9位から28位までの選手のグループを予選敗退グループと呼ぶことにする。決勝進出グループであり、かつ30個のタイムの分散が小さい方から14番目までの選手の人数を $n(\text{人})$ とすると、表2のようになる。

表2　順位と分散の表（単位は人）

		分散（小さい順）		計
		1番～14番	15番～28番
順位	決勝進出グループ	$n$	$8-n$	$8$
	予選敗退グループ	$14-n$	$6+n$	$20$
計		$14$	$14$	$28$

　このとき、図3から $n=\myBox{ト}$ であることがわかる。このことから、決勝進出グループにおいて分散が小さい方から14番目までの選手が占める割合を $P$、予選敗退グループにおいて分散が小さい方から14番目までの選手が占める割合を $Q$ とすると、$P \dBox{ナ} Q$ であることがわかる。

$\dbox{ナ}$ の解答群
　0: $\lt$
　1: $=$
　2: $\gt$

考え方

(3)(i)は外れ値に使う値から四分位範囲を求めるという、通常とは逆の流れです。連立方程式を作って考えましょう。四分位数自体は求めなくても答えを得ることはできます。

(3)(ii)や(iii)は、初めて見るタイプのデータから考える問題です。分散と順位が混ざっていて複雑ですが、一つ一つ定義や問題文などを確認しながら解いていきましょう。

【必答問題】

解答編

問題

　以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。

「(第1四分位数) $- 1.5 \times$ (四分位範囲)」以下の値
「(第3四分位数) $+ 1.5 \times$ (四分位範囲)」以上の値

　水泳部に所属する太郎さんは、1500 $\mathrm{m}$ 自由形におけるペース配分を考えるために、2021年に開催された東京オリンピックの男子 1500 $\mathrm{m}$ 自由形に関するデータを分析することにした。なお、自由形とは、どのような泳ぎ方で泳いでもよい競技のことである。
　分析で用いるデータは、28人の選手における、予選で計測された記録（以下、タイム）とする。ここでは、タイムは秒単位で表すものとする。例えば、15分23秒46であれば、$60 \times 15 + 23.46 = 923.46$ (秒)である。そして、公式順位（以下、順位）は、タイムの値が小さい方が上位となる。また、28人の選手それぞれのタイムについて、スタートから 750 $\mathrm{m}$ までのタイムを $T_{\text{前}}$ とし、750 $\mathrm{m}$ からゴールまでのタイムを $T_{\text{後}}$ とする。さらに、$T_{\text{前}}$ と $T_{\text{後}}$ の平均値を $T_{\text{前後}}$ とする。
　なお、以下の図や表については、World Aquatics の Web ページをもとに作成している。

(1) 太郎さんは、$T_{\text{前}}$、$T_{\text{後}}$、$T_{\text{前後}}$ の関係を調べることにした。図1は $T_{\text{前}}$ と $T_{\text{後}}$ の散布図、図2は $T_{\text{前}}$ と $T_{\text{前後}}$ の散布図である。なお、これらの散布図には、完全に重なっている点はない。また、図1と図2において、Aを付している点は、同じ選手であることを表している。

　次の(a)、(b)は、図1と図2に関する記述である。

(a) $T_{\text{前}}$ が 470 秒未満である選手について、$T_{\text{後}}$ が 460 秒以上である選手の人数と、$T_{\text{前後}}$ が 460 秒以上である選手の人数は等しい。

(b) A を付している点が表す選手について、$T_{\text{前}}$ の値は $T_{\text{前後}}$ の値より小さく、かつ $T_{\text{後}}$ の値は $T_{\text{前後}}$ の値より大きい。

　(a)、(b)の正誤の組合せとして正しいものは $\dBox{ソ}$ である。

$\dbox{ソ}$ の解答群
　0: (a) 正 (b) 正
　1: (a) 正 (b) 誤
　2: (a) 誤 (b) 正
　3: (a) 誤 (b) 誤

解説

(1)
それぞれ確認します。

まず、$T_{\text{前}}$ が470秒未満で、$T_{\text{後}}$ が460秒以上の人数は左の散布図で確認すると、7人だとわかります。

$T_{\text{前}}$ が470秒未満で、$T_{\text{前後}}$ が460秒以上の人数は右の散布図で確認すると、3人だとわかります。なので、(a)は誤です。

A の選手は、右の散布図を見ると、 $T_{\text{前}}$ は 460未満で、$T_{\text{前後}}$ は 460より大きいことがわかるので、「$T_{\text{前}}$ の値は $T_{\text{前後}}$ の値より小さい」といえます。

右の散布図を見ると $T_{\text{前後}}$ は 470未満で、左の散布図を見ると $T_{\text{後}}$ は 470より大きいことがわかるので、「$T_{\text{後}}$ の値は $T_{\text{前後}}$ の値より大きい」といえます。なので、(b)は正です。

解答

ソ：2 （3点）

解答編　つづき

問題

(2) 太郎さんは、$T_{\text{前}}$ と $T_{\text{前後}}$ の相関係数を計算するために、表1のように、平均値、標準偏差および共分散を求めた。

表1　$T_{\text{前}}$ と $T_{\text{前後}}$ の平均値、標準偏差、共分散

	平均値	標準偏差	共分散
$T_{\text{前}}$	450	8.3	72.9
$T_{\text{前後}}$	453	9.3

　表1を用いると、$T_{\text{前}}$ と $T_{\text{前後}}$ の相関係数は $\dBox{タ}$ である。

$\dbox{タ}$ については、最も適当なものを、次の 0 ～ 9 のうちから一つ選べ。
　0: $0.01$
　1: $0.24$
　2: $0.47$
　3: $0.59$
　4: $0.72$
　5: $0.83$
　6: $0.94$
　7: $1.06$
　8: $1.38$
　9: $4.14$

解説

(2)(i)

相関係数は、共分散をそれぞれの標準偏差で割れば求められるので
\begin{eqnarray} \frac{72.9}{8.3\cdot 9.3} &=& 0.944\cdots \end{eqnarray}なので、選択肢の中では $0.94$ が一番近いことがわかります。

解答

タ：6 （3点）

解答編　つづき

問題

(3) 太郎さんは、順位とペース配分の関係を調べるために、前半と後半という二分割だけではなく、より細かく分割されたタイムを用いて分析することにした。1500 $\mathrm{m}$ 自由形のタイムは、スタートから 50 $\mathrm{m}$ までのタイム、50 $\mathrm{m}$ から 100 $\mathrm{m}$ までのタイムのように、ゴールまで 50 $\mathrm{m}$ ごとの 30 個に分けて計測されている。そこで、これら 30 個のタイムを用いて分析する。

(i) 1位の選手の30個のタイムについて考えると、外れ値かどうかを判断する二つの値である $29.315$ と $29.835$ が算出され、$29.315$ 以下の2個のタイムと $29.835$ 以上の1個のタイムが外れ値と判断された。このとき、1位の選手の30個のタイムの四分位範囲は $0.\myBox{チツ}$ 秒である。

解説

(3)(i)
第1四分位数、第3四分位数を、それぞれ $x,y$ とおくと、四分位範囲は $y-x$ なので、冒頭の外れ値の定義から

　・$x-1.5(y-x)$ 以下
　・$y+1.5(y-x)$ 以上

が外れ値となります。外れ値を判断する2つの値が $29.315$ と $29.835$ であることから、まず小さいほうの値について、以下が成り立ちます。
\begin{eqnarray} x-1.5(y-x) &=& 29.315 \\[5pt] 2.5x-1.5y &=& 29.315 \\[5pt] \end{eqnarray}また、大きいほうの値について以下が成り立ちます。 \begin{eqnarray} y+1.5(y-x) &=& 29.835 \\[5pt] -1.5x+2.5y &=& 29.835 \\[5pt] \end{eqnarray}

2つ目から1つ目を辺々引くと
\begin{eqnarray} -4x+4y &=& 0.52 \\[5pt] y-x &=& 0.13 \\[5pt] \end{eqnarray}となることがわかります。左辺は四分位範囲を表しているので、 $0.13$ が答えだとわかります。

解答

チツ：13 （3点）

解答編　つづき

問題

(ii) 太郎さんは28人の選手それぞれについて、30個のタイムを用いて、選手ごとの箱ひげ図を作成し、分散を計算した。図3は上から分散が小さい順になるように、28人の選手それぞれの箱ひげ図を並べたものであり、30個のタイムにおける外れ値は、白丸で示されている。なお、分散が等しい選手はいなかった。

　次の(a)、(b)は、図3に関する記述である。

(a) 28人の選手において、29秒より速いタイムはすべて外れ値である。
(b) 28人の選手から2人を選んだとき、分散の大きい選手の四分位範囲は、分散の小さい選手の四分位範囲より小さいことがある。

　(a)、(b)の正誤の組合せとして正しいものは $\dBox{テ}$ である。

$\dbox{テ}$ の解答群
　0: (a) 正 (b) 正
　1: (a) 正 (b) 誤
　2: (a) 誤 (b) 正
　3: (a) 誤 (b) 誤

解説

(3)(ii)

一番下の21位の選手を見ると、27秒くらいのタイムが最小値となっており、外れ値にはなっていないことがわかります。なので、「29秒より速いタイムはすべて外れ値」とはなっていないので、(a)は誤です。

下側にある22位とその下の11位を比べると、11位のほうが下にあるので11位の分散の方が大きいことがわかりますが、四分位範囲（箱の横幅に対応）は11位の方が小さいことが読み取れます。「分散の大きい選手の四分位範囲は、分散の小さい選手の四分位範囲より小さいことがある」といえるので、(b)は正です。

解答

テ：2 （3点）

解答編　つづき

問題

(iii) 順位が1位から8位までの選手のグループを決勝進出グループ、9位から28位までの選手のグループを予選敗退グループと呼ぶことにする。決勝進出グループであり、かつ30個のタイムの分散が小さい方から14番目までの選手の人数を $n(\text{人})$ とすると、表2のようになる。

表2　順位と分散の表（単位は人）

		分散（小さい順）		計
		1番～14番	15番～28番
順位	決勝進出グループ	$n$	$8-n$	$8$
	予選敗退グループ	$14-n$	$6+n$	$20$
計		$14$	$14$	$28$

　このとき、図3から $n=\myBox{ト}$ であることがわかる。このことから、決勝進出グループにおいて分散が小さい方から14番目までの選手が占める割合を $P$、予選敗退グループにおいて分散が小さい方から14番目までの選手が占める割合を $Q$ とすると、$P \dBox{ナ} Q$ であることがわかる。

$\dbox{ナ}$ の解答群
　0: $\lt$
　1: $=$
　2: $\gt$

解説

(3)(ii)
$n$ とは、8位までの選手で、分散が小さい順から14番目までの選手の人数を表しています。分散の小さい順から14番目は5位の人で、7位の人以外は分散は14番目以内に入っています。なので、 $n=7$ だとわかります。

決勝進出グループは8人、その中で、分散が小さい方から14番目までの選手でもあるのは7人なので、決勝進出グループにおいて分散が小さい方から14番目までの選手が占める割合である $P$ は\[ P=\dfrac{7}{8} \]です。

予選敗退グループは20人、その中で、分散が小さい方から14番目までの選手でもあるのは、 $14-7=7$ 人なので、予選敗退グループにおいて分散が小さい方から14番目までの選手が占める割合である $Q$ は、\[ Q=\dfrac{7}{20} \]です。

なので、 $P\gt Q$ だとわかります。

結局、あまり振れが大きくない人ほど順位が高い、という分析結果となっています。

解答

トナ：72 （3点）