共通テスト 数学I・数学A 2026年度 第2問 [1] 解説
【必答問題】
問題編
問題
2次関数の最大値、最小値について考えよう。
(1) 2次関数 $y=2x^2-8x+5$ は $0 \leqq x \leqq 3$ において、$x=\myBox{ア}$ で最大値 $\myBox{イ}$ をとり、$x=\myBox{ウ}$ で最小値 $\myBox{エオ}$ をとる。
(2) 太郎さんと花子さんは、(1)を振り返って2次関数の最大値、最小値について話している。
- (1)では、2次関数と $x$ のとり得る値の範囲が与えられて、最大値と最小値を求めることができたね。
- じゃあ、$x$ の値の範囲とそのときの最大値と最小値に関する条件が与えられている場合に、条件を満たす2次関数を求めることはできるのかな。具体的な例で考えてみよう。
(i) 2次関数 $y=f(x)$ は次の条件1を満たすとする。
条件1
$y=f(x)$ は $-3 \leqq x \leqq 0$ において
・$x=-1$ で最大値 $3$ をとる。
・$x=-3$ で最小値 $-5$ をとる。このとき、$y=f(x)$ のグラフの頂点の座標は $\dBox{カ}$ であり
\[f(x) = \myBox{キク} x^2 - \myBox{ケ} x + \myBox{コ}\]である。$\dbox{カ}$ の解答群
0: $(0, 3)$
1: $(1, 3)$
2: $(3, 3)$
3: $(-1, 3)$
4: $(-3, 3)$
5: $(0, -5)$
6: $(1, -5)$
7: $(3, -5)$
8: $(-1, -5)$
9: $(-3, -5)$(ii) 2次関数 $y=g(x)$ は次の条件2を満たすとする。
条件2
$a$ を正の定数とし、$y=g(x)$ の $0 \leqq x \leqq a$ における最大値を $M$、最小値を $m$ とすると
・$0 \lt a \lt 3$ ならば、$m > -2$ である。
・$a \geqq 3$ ならば、$m = -2$ である。
・$0 \lt a \leqq 6$ ならば、$M = 7$ である。
・$a \gt 6$ ならば、$M \gt 7$ である。このとき、2次関数 $y=g(x)$ のグラフは $\dBox{サ}$ の放物線であり
\[g(x) = \dBox{シ}\]である。$\dbox{サ}$ の解答群
0: 下に凸
1: 上に凸$\dbox{シ}$ の解答群
0: $2x^2-12x+16$
1: $-2x^2+12x-16$
2: $2x^2-12x-16$
3: $-2x^2+12x-20$
4: $x^2-7$
5: $-x^2+7$
6: $x^2-6x+7$
7: $-x^2+6x-7$
8: $2x^2-9x+7$
9: $-2x^2+3x+7$(3) 2次関数 $y=h(x)$ は次の条件3を満たすとする。
条件3
$b$ を定数とし、$y=h(x)$ の $b-1 \leqq x \leqq b+1$ における最大値を $M$ とすると
・$1 \leqq b \leqq 7$ ならば、$M \geqq 0$ である。
・$b \lt 1$ または $7 \lt b$ ならば、$M \lt 0$ である。太郎さんと花子さんは $h(x)$ について話している。
- (2)の条件1や条件2からは関数が一つに決まったけど、条件3だけでは、$h(x)$ が一つに決まりそうにないね。
- でも、$y=h(x)$ のグラフと $x$ 軸の共有点の座標はわかりそうだね。
2次関数 $y=h(x)$ のグラフと $x$ 軸の共有点の $x$ 座標は $\myBox{ス}$ および $\myBox{セ}$ である。ただし、$\mybox{ス}$、$\mybox{セ}$ の解答の順序は問わない。
考え方
そもそも区間に文字が入っている二次関数の最大値・最小値は多くの人が苦手としていますが、この問題ではさらにひねって、最大値・最小値からもとの関数を考える、という形式になっています。
どういう状況で最大値・最小値をとるか、その状況がどこで切り替わるかに注目して考えればよく、やることは同じといえば同じなのですが、係数や区間に文字が入ったときの最大値・最小値の問題をよく練習していないと難しく感じるかもしれません。
【必答問題】
解答編
問題
2次関数の最大値、最小値について考えよう。
(1) 2次関数 $y=2x^2-8x+5$ は $0 \leqq x \leqq 3$ において、$x=\myBox{ア}$ で最大値 $\myBox{イ}$ をとり、$x=\myBox{ウ}$ で最小値 $\myBox{エオ}$ をとる。
解説
(1)
\begin{eqnarray}
y &=& 2x^2-8x+5 \\[5pt]
&=& 2(x^2-4x)+5 \\[5pt]
&=& 2\{(x-2)^2-4\}+5 \\[5pt]
&=& 2(x-2)^2-8+5 \\[5pt]
&=& 2(x-2)^2-3 \\[5pt]
\end{eqnarray}なので、 $0\leqq x\leqq 3$ でのグラフは次のようになります。
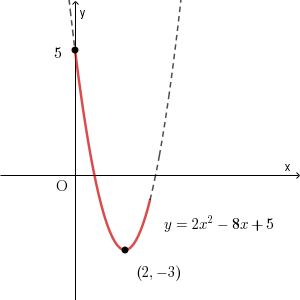
これより、 $x=0$ のときに最大値 $5$ をとり、 $x=2$ のときに最小値 $-3$ をとることがわかります。
解答
アイ:05 (2点)
ウエオ:2-3 (2点)
解答編 つづき
問題
(2) 太郎さんと花子さんは、(1)を振り返って2次関数の最大値、最小値について話している。
- (1)では、2次関数と $x$ のとり得る値の範囲が与えられて、最大値と最小値を求めることができたね。
- じゃあ、$x$ の値の範囲とそのときの最大値と最小値に関する条件が与えられている場合に、条件を満たす2次関数を求めることはできるのかな。具体的な例で考えてみよう。
(i) 2次関数 $y=f(x)$ は次の条件1を満たすとする。
条件1
$y=f(x)$ は $-3 \leqq x \leqq 0$ において
・$x=-1$ で最大値 $3$ をとる。
・$x=-3$ で最小値 $-5$ をとる。このとき、$y=f(x)$ のグラフの頂点の座標は $\dBox{カ}$ であり
\[f(x) = \myBox{キク} x^2 - \myBox{ケ} x + \myBox{コ}\]である。$\dbox{カ}$ の解答群
0: $(0, 3)$
1: $(1, 3)$
2: $(3, 3)$
3: $(-1, 3)$
4: $(-3, 3)$
5: $(0, -5)$
6: $(1, -5)$
7: $(3, -5)$
8: $(-1, -5)$
9: $(-3, -5)$
解説
(2)(i)
$-3\leqq x\leqq 0$ の区間において、 $x=-1$ で最大値をとることに注目して考えます。
二次関数のグラフが下に凸( $x^2$ の係数が正)の場合、最大値は区間の端でとります。条件1では、区間の端で最大値をとっているわけではないので、下に凸ではないことがわかります。なので、上に凸、つまり、 $x^2$ の係数は負であることがわかります。
上に凸で、区間の端ではないところで最大値をとっているので、最大値をとるところが頂点だとわかります。つまり、頂点の座標は\[ (-1,3) \]だとわかります。
頂点がわかったので、 $x^2$ の係数を $a$ とおくと、 $f(x)$ は次のように書けます。\[ f(x)=a(x+1)^2+3 \]ここで、もう1つの条件、最小値の条件を代入すると
\begin{eqnarray}
-5 &=& a(-3+1)^2+3 \\[5pt]
-5 &=& 4a+3 \\[5pt]
4a &=& -8 \\[5pt]
a &=& -2 \\[5pt]
\end{eqnarray}となることがわかります。
こうして、
\begin{eqnarray}
f(x) &=& -2(x+1)^2+3 \\[5pt]
&=& -2(x^2+2x+1)+3 \\[5pt]
&=& -2x^2-4x+1 \\[5pt]
\end{eqnarray}と求められます。
解答
カ:3 (2点)
キクケコ:-241 (2点)
解答編 つづき
問題
(ii) 2次関数 $y=g(x)$ は次の条件2を満たすとする。
条件2
$a$ を正の定数とし、$y=g(x)$ の $0 \leqq x \leqq a$ における最大値を $M$、最小値を $m$ とすると
・$0 \lt a \lt 3$ ならば、$m > -2$ である。
・$a \geqq 3$ ならば、$m = -2$ である。
・$0 \lt a \leqq 6$ ならば、$M = 7$ である。
・$a \gt 6$ ならば、$M \gt 7$ である。このとき、2次関数 $y=g(x)$ のグラフは $\dBox{サ}$ の放物線であり
\[g(x) = \dBox{シ}\]である。$\dbox{サ}$ の解答群
0: 下に凸
1: 上に凸$\dbox{シ}$ の解答群
0: $2x^2-12x+16$
1: $-2x^2+12x-16$
2: $2x^2-12x-16$
3: $-2x^2+12x-20$
4: $x^2-7$
5: $-x^2+7$
6: $x^2-6x+7$
7: $-x^2+6x-7$
8: $2x^2-9x+7$
9: $-2x^2+3x+7$
解説
(2)(ii)
$0\leqq x\leqq a$ における最小値 $m$ について、 $a\geqq 3$ ならば $m=-2$ という条件があります。範囲をどんどん広げていっても最小値が変わらない、ということは、上に凸ではないこと、つまり、下に凸であることがわかります。 $x^2$ の係数は正です。
下に凸の場合、区間の端か頂点で最小値をとります。 $a\geqq 3$ なら最小値がかわらないということは、 $x=3$ のところが頂点だということです。なので、 $g(x)$ の $x^2$ の係数を $a$ とすると\[ g(x)=a(x-3)^2-2 \]となることがわかります。なお、 $a\gt 0$ です。
最大値に関する条件を考えます。 $0\lt a\leqq 6$ での最大値が $M=7$ であるということは、 $a=3$ のときでも最大値が $M=7$ だということです。右端が頂点なので、最大値は $x=0$ のときにとることがわかります。なので、
\begin{eqnarray}
7 &=& a(0-3)^2-2 \\[5pt]
7 &=& 9a-2 \\[5pt]
a &=& 1 \\[5pt]
\end{eqnarray}となることがわかります。こうして
\begin{eqnarray}
g(x) &=& (x-3)^2-2 \\[5pt]
&=& x^2-6x+7 \\[5pt]
\end{eqnarray}と求められます。
解答
サシ:06 (4点)
解答編 つづき
問題
(3) 2次関数 $y=h(x)$ は次の条件3を満たすとする。
条件3
$b$ を定数とし、$y=h(x)$ の $b-1 \leqq x \leqq b+1$ における最大値を $M$ とすると
・$1 \leqq b \leqq 7$ ならば、$M \geqq 0$ である。
・$b \lt 1$ または $7 \lt b$ ならば、$M \lt 0$ である。太郎さんと花子さんは $h(x)$ について話している。
- (2)の条件1や条件2からは関数が一つに決まったけど、条件3だけでは、$h(x)$ が一つに決まりそうにないね。
- でも、$y=h(x)$ のグラフと $x$ 軸の共有点の座標はわかりそうだね。
2次関数 $y=h(x)$ のグラフと $x$ 軸の共有点の $x$ 座標は $\myBox{ス}$ および $\myBox{セ}$ である。ただし、$\mybox{ス}$、$\mybox{セ}$ の解答の順序は問わない。
解説
(3)
まず、 $b\gt 7$ のときは最大値が負であるということは、グラフの右のほうはずっと $x$ 軸の下にあるということだから、グラフは上に凸だとわかります。
次に、状況が変わる境目を考えてみます。 $b=7$ のとき、 $6\leqq x\leqq 8$ における最大値が $0$ 以上なのに、 $b$ が $7$ より少し大きくなったら、もう最大値は負になってしまう、ということなので、グラフは次のようになっていることがわかります。
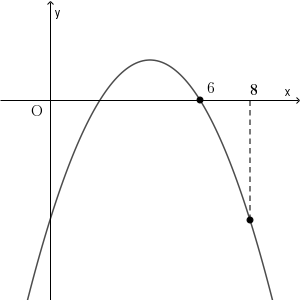
$b-1\leqq x\leqq b+1$ が $b=7$ のときから少し右に行っただけで、最大値が負になってしまうので、上のような状況だとわかります。
一方、 $b=1$ のときも同様です。 $0\leqq x\leqq 2$ のときの最大値が $0$ 以上なのに、この範囲が少し左に行っただけで最大値が負になってしまうということは、 $x=2$ のところで $y=0$ となることがわかります。
なので、 $y=h(x)$ と $x$ 軸との共有点の $x$ 座標は $2$ と $6$ だとわかります。
解答
ス・セ:2・6 (3点)





