共通テスト数学I・数学A 2026年度第1問 [2] 解説

🕒 2026/01/18

【必答問題】

問題編

問題

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) 四角形 $\mathrm{ABCD}$ の面積 $S$ について考えよう。以下では、四角形 $\mathrm{ABCD}$ の内角 $\angle \mathrm{A}$、$\angle \mathrm{B}$、$\angle \mathrm{C}$、$\angle \mathrm{D}$ の大きさを、それぞれ $A$、$B$、$C$、$D$ で表す。ただし、四つの内角はいずれも $180^{\circ}$ より小さいものとする。
　対角線 $\mathrm{BD}$ を共通の1辺とする $\triangle \mathrm{ABD}$ と $\triangle \mathrm{BCD}$ の面積を、それぞれ $S_1$、$S_2$ とすると
\[S_1 = \dfrac{\dBox{ク}}{2} \sin A, \quad S_2 = \dfrac{\dBox{ケ}}{2} \sin C\]となる。
　四角形 $\mathrm{ABCD}$ の四つの内角が $A+C = B+D$ を満たすとき、
$A+C = \dBox{コ}$ となる。このとき、$\sin C$ を $\sin A$ を用いて表せることに注意すると
\[S = S_1 + S_2 = \dfrac{\dBox{サ}}{2} \sin A \quad \cdots\cdots \text{①}\]となる。

$\dbox{ク},$ $\dbox{ケ}$ の解答群（同じものを繰り返し選んでもよい。）
　0: $\mathrm{AB} \cdot \mathrm{BD}$
　1: $\mathrm{AB} \cdot \mathrm{AD}$
　2: $\mathrm{AD} \cdot \mathrm{BD}$
　3: $\mathrm{BC} \cdot \mathrm{BD}$
　4: $\mathrm{BC} \cdot \mathrm{CD}$
　5: $\mathrm{BD} \cdot \mathrm{CD}$
　6: $\mathrm{AB} \cdot \mathrm{CD}$
　7: $\mathrm{AD} \cdot \mathrm{BC}$
　8: $\mathrm{AC} \cdot \mathrm{BD}$

$\dbox{コ}$ の解答群
　0: $90^{\circ}$
　1: $120^{\circ}$
　2: $135^{\circ}$
　3: $150^{\circ}$
　4: $180^{\circ}$
　5: $240^{\circ}$
　6: $270^{\circ}$
　7: $360^{\circ}$

$\dbox{サ}$ の解答群
　0: $\mathrm{AB} \cdot \mathrm{BD} + \mathrm{BC} \cdot \mathrm{BD}$
　1: $\mathrm{AB} \cdot \mathrm{BD} - \mathrm{BC} \cdot \mathrm{BD}$
　2: $\mathrm{AB} \cdot \mathrm{AD} + \mathrm{BC} \cdot \mathrm{CD}$
　3: $\mathrm{AB} \cdot \mathrm{AD} - \mathrm{BC} \cdot \mathrm{CD}$
　4: $\mathrm{AD} \cdot \mathrm{BD} + \mathrm{BD} \cdot \mathrm{CD}$
　5: $\mathrm{AD} \cdot \mathrm{BD} - \mathrm{BD} \cdot \mathrm{CD}$
　6: $\mathrm{AB} \cdot \mathrm{CD} + \mathrm{AD} \cdot \mathrm{BC}$
　7: $\mathrm{AB} \cdot \mathrm{CD} - \mathrm{AD} \cdot \mathrm{BC}$
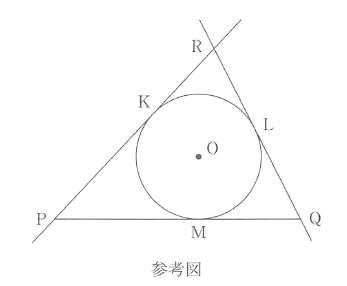
　8: $\mathrm{AC} \cdot \mathrm{BD}$

(2) 点 $\mathrm{O}$ を中心とする半径 $6$ の円 $\mathrm{O}$ が、線分 $\mathrm{PQ}$ 上の $\mathrm{P}$、$\mathrm{Q}$ と異なる点 $\mathrm{M}$ において線分 $\mathrm{PQ}$ に接している。$\mathrm{P}$、$\mathrm{Q}$ それぞれを通る円 $\mathrm{O}$ の接線で、直線 $\mathrm{PQ}$ と異なるものを引き、この円との接点をそれぞれ $\mathrm{K}$、$\mathrm{L}$ とする。以下では直線 $\mathrm{PK}$、$\mathrm{QL}$ が交わる場合を考え、その交点を $\mathrm{R}$ とする。このとき、$\triangle \mathrm{PQR}$ の辺の長さについて考えよう。

(i) $\mathrm{PK} = 12$、$\mathrm{QL} = 9$ であるときを考え、$\angle \mathrm{KPM} = P$、$\angle \mathrm{LQM} = Q$ とする。このとき、2直線 $\mathrm{PK}$、$\mathrm{QL}$ の交点 $\mathrm{R}$ は直線 $\mathrm{PQ}$ に関して点 $\mathrm{O}$ と同じ側にある。

　四角形 $\mathrm{PMOK}$ が $\triangle \mathrm{PMO}$ と $\triangle \mathrm{PKO}$ に分けられることに注意すると、四角形 $\mathrm{PMOK}$ の面積は $\myBox{シス}$ であることがわかる。このことから、① を用いると、$\sin P = \dfrac{\myBox{セ}}{\myBox{ソ}}$ となることがわかる。
　四角形 $\mathrm{QLOM}$ についても同様に考えると、$\sin Q = \dfrac{\myBox{タチ}}{\myBox{ツテ}}$ となることもわかる。よって、$\mathrm{PR} : \mathrm{QR} = \myBox{トナ} : \myBox{ニヌ}$ となり、これにより
\[\mathrm{RL} = \dfrac{\myBox{ネノ}}{\myBox{ハ}}\]と求められるので、$\triangle \mathrm{PQR}$ の辺の長さを求めることができる。

(ii) $\mathrm{PK} = 4\sqrt{2}$、$\mathrm{QL} = 3\sqrt{2}$ であるときを考える。このとき、2直線 $\mathrm{PK}$、$\mathrm{QL}$ の交点 $\mathrm{R}$ は、直線 $\mathrm{PQ}$ に関して点 $\mathrm{O}$ と反対側にある。このことに注意すると $\mathrm{RL} = \myBox{ヒフ} \sqrt{\myBox{ヘ}}$ と求められるので、$\triangle \mathrm{PQR}$ の辺の長さを求めることができる。

考え方

(2)(i)が(1)とどう関係するのか、少しわかりづらいかもしれません。線をかきこんで、四角形を作って考えるとわかりやすいです。

$\sin$ から辺の比をどう出すかが少し難しく、それをクリアしても $\mathrm{RL}$ をどう出すかがまた難しいです。比を表すことを考えましょう。内接円の性質も少し使います。

(2)(ii)は、(i)の応用ですが、まず図がかきづらいです。(i)と状況が違う、というヒントはある者の、(i)でやった計算を再びやらないといけないし、(i)との違いが、どの部分に表れるのかを自分で思いつかないといけないです。難しくて時間もかかる上に、解答が1個だけと、効率の悪い問題です。

【必答問題】

解答編

問題

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) 四角形 $\mathrm{ABCD}$ の面積 $S$ について考えよう。以下では、四角形 $\mathrm{ABCD}$ の内角 $\angle \mathrm{A}$、$\angle \mathrm{B}$、$\angle \mathrm{C}$、$\angle \mathrm{D}$ の大きさを、それぞれ $A$、$B$、$C$、$D$ で表す。ただし、四つの内角はいずれも $180^{\circ}$ より小さいものとする。
　対角線 $\mathrm{BD}$ を共通の1辺とする $\triangle \mathrm{ABD}$ と $\triangle \mathrm{BCD}$ の面積を、それぞれ $S_1$、$S_2$ とすると
\[S_1 = \dfrac{\dBox{ク}}{2} \sin A, \quad S_2 = \dfrac{\dBox{ケ}}{2} \sin C\]となる。
　四角形 $\mathrm{ABCD}$ の四つの内角が $A+C = B+D$ を満たすとき、
$A+C = \dBox{コ}$ となる。このとき、$\sin C$ を $\sin A$ を用いて表せることに注意すると
\[S = S_1 + S_2 = \dfrac{\dBox{サ}}{2} \sin A \quad \cdots\cdots \text{①}\]となる。

$\dbox{ク},$ $\dbox{ケ}$ の解答群（同じものを繰り返し選んでもよい。）
　0: $\mathrm{AB} \cdot \mathrm{BD}$
　1: $\mathrm{AB} \cdot \mathrm{AD}$
　2: $\mathrm{AD} \cdot \mathrm{BD}$
　3: $\mathrm{BC} \cdot \mathrm{BD}$
　4: $\mathrm{BC} \cdot \mathrm{CD}$
　5: $\mathrm{BD} \cdot \mathrm{CD}$
　6: $\mathrm{AB} \cdot \mathrm{CD}$
　7: $\mathrm{AD} \cdot \mathrm{BC}$
　8: $\mathrm{AC} \cdot \mathrm{BD}$

$\dbox{コ}$ の解答群
　0: $90^{\circ}$
　1: $120^{\circ}$
　2: $135^{\circ}$
　3: $150^{\circ}$
　4: $180^{\circ}$
　5: $240^{\circ}$
　6: $270^{\circ}$
　7: $360^{\circ}$

$\dbox{サ}$ の解答群
　0: $\mathrm{AB} \cdot \mathrm{BD} + \mathrm{BC} \cdot \mathrm{BD}$
　1: $\mathrm{AB} \cdot \mathrm{BD} - \mathrm{BC} \cdot \mathrm{BD}$
　2: $\mathrm{AB} \cdot \mathrm{AD} + \mathrm{BC} \cdot \mathrm{CD}$
　3: $\mathrm{AB} \cdot \mathrm{AD} - \mathrm{BC} \cdot \mathrm{CD}$
　4: $\mathrm{AD} \cdot \mathrm{BD} + \mathrm{BD} \cdot \mathrm{CD}$
　5: $\mathrm{AD} \cdot \mathrm{BD} - \mathrm{BD} \cdot \mathrm{CD}$
　6: $\mathrm{AB} \cdot \mathrm{CD} + \mathrm{AD} \cdot \mathrm{BC}$
　7: $\mathrm{AB} \cdot \mathrm{CD} - \mathrm{AD} \cdot \mathrm{BC}$
　8: $\mathrm{AC} \cdot \mathrm{BD}$

解説

(1)
$\mathrm{A}$ をはさむ2辺を使って、面積は\[ S_1=\frac{1}{2}\mathrm{AB\cdot AD}\sin A \]と書くことができます。同様に、\[ S_2=\frac{1}{2}\mathrm{BC\cdot CD}\sin C \]となります。

4つの内角の和は $360^{\circ}$ なので、 $A+B+C+D=360^{\circ}$ です。なので、 $A+C=B+D$ とすると、 $2(A+C)=360^{\circ}$ なので、\[ A+C=180^{\circ} \]となります。

$C=180^{\circ}-A$ なので、 $\sin A=\sin C$ が成り立つから
\begin{eqnarray} S &=& S_1+S_2 \\[5pt] &=& \dfrac{\mathrm{AB\cdot AD}+\mathrm{BC\cdot CD}}{2} \sin A \end{eqnarray}となります。

解答

ク：1 （2点）
ケ：4 （2点）
コサ：42 （3点）

解答編　つづき

問題

(2) 点 $\mathrm{O}$ を中心とする半径 $6$ の円 $\mathrm{O}$ が、線分 $\mathrm{PQ}$ 上の $\mathrm{P}$、$\mathrm{Q}$ と異なる点 $\mathrm{M}$ において線分 $\mathrm{PQ}$ に接している。$\mathrm{P}$、$\mathrm{Q}$ それぞれを通る円 $\mathrm{O}$ の接線で、直線 $\mathrm{PQ}$ と異なるものを引き、この円との接点をそれぞれ $\mathrm{K}$、$\mathrm{L}$ とする。以下では直線 $\mathrm{PK}$、$\mathrm{QL}$ が交わる場合を考え、その交点を $\mathrm{R}$ とする。このとき、$\triangle \mathrm{PQR}$ の辺の長さについて考えよう。

(i) $\mathrm{PK} = 12$、$\mathrm{QL} = 9$ であるときを考え、$\angle \mathrm{KPM} = P$、$\angle \mathrm{LQM} = Q$ とする。このとき、2直線 $\mathrm{PK}$、$\mathrm{QL}$ の交点 $\mathrm{R}$ は直線 $\mathrm{PQ}$ に関して点 $\mathrm{O}$ と同じ側にある。

　四角形 $\mathrm{PMOK}$ が $\triangle \mathrm{PMO}$ と $\triangle \mathrm{PKO}$ に分けられることに注意すると、四角形 $\mathrm{PMOK}$ の面積は $\myBox{シス}$ であることがわかる。このことから、① を用いると、$\sin P = \dfrac{\myBox{セ}}{\myBox{ソ}}$ となることがわかる。
　四角形 $\mathrm{QLOM}$ についても同様に考えると、$\sin Q = \dfrac{\myBox{タチ}}{\myBox{ツテ}}$ となることもわかる。よって、$\mathrm{PR} : \mathrm{QR} = \myBox{トナ} : \myBox{ニヌ}$ となり、これにより
\[\mathrm{RL} = \dfrac{\myBox{ネノ}}{\myBox{ハ}}\]と求められるので、$\triangle \mathrm{PQR}$ の辺の長さを求めることができる。

解説

(2)(i)

$\mathrm{PK}$ は接線なので、 $\mathrm{PK}\perp\mathrm{OK}$ となります。

$\triangle\mathrm{PKO}$ は、底辺が $\mathrm{PK}=12$ で、高さが $\mathrm{KO}=6$ の直角三角形と考えることができます。また、この三角形は $\triangle\mathrm{PMO}$ と合同なので、四角形 $\mathrm{PMOK}$ の面積は\[ 12\cdot6=72 \]と求められます。

四角形 $\mathrm{PMOK}$ は向かい合う角の和が $180^{\circ}$ なので、(1)を使うことができて
\begin{eqnarray} 72 &=& \dfrac{12\cdot 12+6\cdot 6}{2} \sin P \\[5pt] 72 &=& 90 \sin P \\[5pt] \sin P &=& \frac{4}{5} \\[5pt] \end{eqnarray}と求められます。なお、 $\sin P$ を求めるために、数学IIの倍角の公式を使うという手もあります。

同様に、四角形 $\mathrm{QLOM}$ の面積は\[ 9\cdot6=54 \]と求められます。これも、向かい合う角の和が $180^{\circ}$ なので、(1)を使って
\begin{eqnarray} 54 &=& \dfrac{9\cdot 9+6\cdot 6}{2} \sin Q \\[5pt] 54 &=& \dfrac{127}{2} \sin Q \\[5pt] \sin Q &=& \frac{12}{13} \\[5pt] \end{eqnarray}と求められます。

$\mathrm{R}$ から $\mathrm{PQ}$ に垂線を下ろし、その足を $\mathrm{H}$ とすると、
\begin{eqnarray} \sin P:\sin Q &=& \dfrac{\mathrm{RH}}{\mathrm{PR}} : \dfrac{\mathrm{RH}}{\mathrm{RQ}} \\[5pt] &=& \mathrm{RQ} : \mathrm{PR} \\[5pt] \end{eqnarray}なので、 \begin{eqnarray} \mathrm{PR} : \mathrm{RQ} &=& \sin Q:\sin P \\[5pt] &=& \frac{12}{13}:\frac{4}{5} \\[5pt] &=& 15:13 \\[5pt] \end{eqnarray}となります。

$\mathrm{RL}=x $ とすると、内接円の性質から $\mathrm{KR=RL}$ なので
\begin{eqnarray} \mathrm{PR} : \mathrm{RQ} &=& 15:13 \\[5pt] (\mathrm{PK}+\mathrm{KR}) : (\mathrm{RL}+\mathrm{LQ}) &=& 15:13 \\[5pt] (12+x) : (x+9) &=& 15:13 \\[5pt] 15(x+9) &=& 13(12+x) \\[5pt] 15x+135 &=& 156+13x \\[5pt] 2x &=& 21 \\[5pt] x &=& \frac{21}{2} \\[5pt] \end{eqnarray}と求められます。

解答

シスセソ：7245 （3点）
タチツテ：1213 （2点）
トナニヌ：1513 （2点）
ネノハ：212 （2点）

解答編　つづき

問題

(ii) $\mathrm{PK} = 4\sqrt{2}$、$\mathrm{QL} = 3\sqrt{2}$ であるときを考える。このとき、2直線 $\mathrm{PK}$、$\mathrm{QL}$ の交点 $\mathrm{R}$ は、直線 $\mathrm{PQ}$ に関して点 $\mathrm{O}$ と反対側にある。このことに注意すると $\mathrm{RL} = \myBox{ヒフ} \sqrt{\myBox{ヘ}}$ と求められるので、$\triangle \mathrm{PQR}$ の辺の長さを求めることができる。

解説

(2)(ii)

図はこのようになっています。

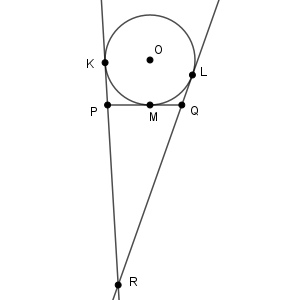
(i)と同じように、四角形 $\mathrm{PMOK}$ の面積と(1)を使うと
\begin{eqnarray} 4\sqrt{2}\cdot 6 &=& \frac{4\sqrt{2}\cdot 4\sqrt{2}+6\cdot 6}{2} \sin P \\[5pt] 24\sqrt{2} &=& 34 \sin P \\[5pt] \sin P &=& \frac{12\sqrt{2}}{17} \\[5pt] \end{eqnarray}となります。

四角形 $\mathrm{QLOM}$ の面積と(1)を使うと
\begin{eqnarray} 3\sqrt{2}\cdot 6 &=& \frac{3\sqrt{2}\cdot 3\sqrt{2}+6\cdot 6}{2} \sin Q \\[5pt] 18\sqrt{2} &=& 27 \sin Q \\[5pt] \sin Q &=& \frac{2\sqrt{2}}{3} \\[5pt] \end{eqnarray}となります。

$\mathrm{R}$ の位置が先ほどと逆になっていますが、三角形 $\mathrm{PQR}$ について先ほどと同じように垂線を引いて考えれば
\begin{eqnarray} \mathrm{PR} : \mathrm{RQ} &=& \sin Q:\sin P \\[5pt] &=& \frac{2\sqrt{2}}{3} : \frac{12\sqrt{2}}{17} \\[5pt] &=& 17 : 18 \\[5pt] \end{eqnarray}となることがわかります。

$\mathrm{RL}=\mathrm{RK}=x$ とすると
\begin{eqnarray} (x-4\sqrt{2}):(x-3\sqrt{2}) &=& 17:18 \\[5pt] 18(x-4\sqrt{2}) &=& 17(x-3\sqrt{2}) \\[5pt] 18x-72\sqrt{2} &=& 17xx-51\sqrt{2} \\[5pt] x &=& 21\sqrt{2} \\[5pt] \end{eqnarray}と求められます。