共通テスト 数学I・数学A 2025年度 第3問 解説

【必答問題】

問題編

問題

　$6$ 点 $\mathrm{A,B,C,D,E,F}$ を頂点とし、三角形 $\mathrm{ABC}$ と $\mathrm{DEF}$、 および四角形 $\mathrm{ABED,ACFD,BCFE}$ を面とする五面体がある。ただし、直線 $\mathrm{AD}$ と $\mathrm{BE}$ は平行でないとする。

　以下では、例えば、面 $\mathrm{ABC}$ を含む平面を平面 $\mathrm{ABC}$、面 $\mathrm{ABED}$ を含む平面を平面 $\mathrm{ABED}$、などということにする。

(1) 3直線 $\mathrm{AD,BE,CF}$ は1点で交わる。これを証明しよう。

　直線 $\mathrm{AD}$ と $\mathrm{BE}$ は平面 $\mathrm{ABED}$ 上にあり、平行でないので1点で交わる。その交点を $\mathrm{P}$ とする。

　点 $\mathrm{P}$ は直線 $\mathrm{AD}$ 上にあり、直線 $\mathrm{AD}$ は平面 $\mathrm{ABED}$ と平面 $\dBox{ア}$ との交線であるから、点 $\mathrm{P}$ は平面 $\dbox{ア}$ 上にあることがわかる。

　また、点 $\mathrm{P}$ は直線 $\mathrm{BE}$ 上にあり、直線 $\mathrm{BE}$ は平面 $\mathrm{ABED}$ と平面 $\dBox{イ}$ との交線であるから、点 $\mathrm{P}$ は平面 $\dbox{イ}$ 上にあることがわかる。

　平面 $\dbox{ア}$ と平面 $\dbox{イ}$ との交線は直線 $\mathrm{CF}$ であるから、点 $\mathrm{P}$ は直線 $\mathrm{CF}$ 上にもあることがわかる。したがって、3直線 $\mathrm{AD,BE,CF}$ は点 $\mathrm{P}$ で交わる。

$\dbox{ア},\ \dbox{イ}$ の解答群（同じものを繰り返し選んでもよい。）
　0: $\mathrm{ABC}$
　1: $\mathrm{DEF}$
　2: $\mathrm{ACFD}$
　3: $\mathrm{BCFE}$

(2) 五面体において、面 $\mathrm{ABC}$ は一辺の長さが $3$ の正三角形であり、\[ \mathrm{AD=7,\ BE=11,\ CF=17,\ DE=9} \]であるとする。また、6点 $\mathrm{A,B,C,D,E,F}$ はある一つの球面上にあるとし、その球面を $\mathrm{S}$ とする。直線 $\mathrm{AD}$ と $\mathrm{BE}$ の交点を $\mathrm{P}$ とする。

(i) 平面 $\mathrm{ABED}$ と球面 $S$ が交わる部分は円であり、4点 $\mathrm{A,B,E,D}$ はその円周上にある。このことから、三角形 $\mathrm{PAB}$ と $\mathrm{PED}$ は相似であることがわかり、その相似比は $1:\myBox{ウ}$ である。したがって
\begin{eqnarray} \mybox{ウ} \mathrm{PA} &=& \mathrm{PB}+\myBox{エオ} \\[5pt] \mybox{ウ} \mathrm{PB} &=& \mathrm{PA}+\myBox{カ} \\[5pt] \end{eqnarray} が成り立つ。よって\[ \mathrm{PA}=\myBox{キ},\ \mathrm{PB}=\myBox{ク} \]となる。

(ii) 平面 $\mathrm{BCFE}$ と球面 $S$ が交わる部分に着目すると、方べきの定理より\[ \mathrm{PC}=\myBox{ケ} \]となる。したがって\[ \mathrm{EF}=\myBox{コサ},\ \mathrm{DF}=\myBox{シス} \]となる。

(iii) $\angle\mathrm{ADE}, \angle\mathrm{ADF}, \angle\mathrm{EDF}$ の大きさに着目すると、次の命題(a), (b), (c) の真偽の組合せとして正しいものは $\dBox{セ}$ であることがわかる。

　(a) 平面 $\mathrm{ABED}$ と平面 $\mathrm{DEF}$ は垂直である。
　(b) 直線 $\mathrm{DE}$ は平面 $\mathrm{ACFD}$ に垂直である。
　(c) 直線 $\mathrm{AC}$ と直線 $\mathrm{DE}$ は垂直である。

$\dbox{セ}$ の解答群

　0: (a)真　(b)真　(c)真
　1: (a)真　(b)真　(c)偽
　2: (a)真　(b)偽　(c)真
　3: (a)真　(b)偽　(c)偽
　4: (a)偽　(b)真　(c)真
　5: (a)偽　(b)真　(c)偽
　6: (a)偽　(b)偽　(c)真
　7: (a)偽　(b)偽　(c)偽

考え方

(2)の(i)や(ii)は、平面で切って考えると、ただの平面図形の問題になります。空間図形だと思って嫌がらずに考えていきましょう。

(2)の(iii)は少し考えづらいですが、長さから角度がどうなっているかを考えましょう。まずは直線と直線のなす角を考えて、それを求めに平面と直線のなす角などを考えていきましょう。

【必答問題】

解答編

問題

　$6$ 点 $\mathrm{A,B,C,D,E,F}$ を頂点とし、三角形 $\mathrm{ABC}$ と $\mathrm{DEF}$、 および四角形 $\mathrm{ABED,ACFD,BCFE}$ を面とする五面体がある。ただし、直線 $\mathrm{AD}$ と $\mathrm{BE}$ は平行でないとする。

　以下では、例えば、面 $\mathrm{ABC}$ を含む平面を平面 $\mathrm{ABC}$、面 $\mathrm{ABED}$ を含む平面を平面 $\mathrm{ABED}$、などということにする。

(1) 3直線 $\mathrm{AD,BE,CF}$ は1点で交わる。これを証明しよう。

　直線 $\mathrm{AD}$ と $\mathrm{BE}$ は平面 $\mathrm{ABED}$ 上にあり、平行でないので1点で交わる。その交点を $\mathrm{P}$ とする。

　点 $\mathrm{P}$ は直線 $\mathrm{AD}$ 上にあり、直線 $\mathrm{AD}$ は平面 $\mathrm{ABED}$ と平面 $\dBox{ア}$ との交線であるから、点 $\mathrm{P}$ は平面 $\dbox{ア}$ 上にあることがわかる。

　また、点 $\mathrm{P}$ は直線 $\mathrm{BE}$ 上にあり、直線 $\mathrm{BE}$ は平面 $\mathrm{ABED}$ と平面 $\dBox{イ}$ との交線であるから、点 $\mathrm{P}$ は平面 $\dbox{イ}$ 上にあることがわかる。

　平面 $\dbox{ア}$ と平面 $\dbox{イ}$ との交線は直線 $\mathrm{CF}$ であるから、点 $\mathrm{P}$ は直線 $\mathrm{CF}$ 上にもあることがわかる。したがって、3直線 $\mathrm{AD,BE,CF}$ は点 $\mathrm{P}$ で交わる。

$\dbox{ア},\ \dbox{イ}$ の解答群（同じものを繰り返し選んでもよい。）
　0: $\mathrm{ABC}$
　1: $\mathrm{DEF}$
　2: $\mathrm{ACFD}$
　3: $\mathrm{BCFE}$

解説

(1)

直線 $\mathrm{AD}$ は平面 $\mathrm{ABED}$ と平面 $\mathrm{ACFD}$ との交線なので、点 $\mathrm{P}$ は平面 $\mathrm{ACFD}$ 上にあります。

また、直線 $\mathrm{BE}$ は平面 $\mathrm{ABED}$ と平面 $\mathrm{BCFE}$ との交線なので、点 $\mathrm{P}$ は平面 $\mathrm{BCFE}$ 上にあります。

直線 $\mathrm{CF}$ は平面 $\mathrm{ACFD}$ と平面 $\mathrm{BCFE}$ との交線だから、点 $\mathrm{P}$ は 直線 $\mathrm{CF}$ 上にあることもわかるので、3直線 $\mathrm{AD},\mathrm{BE},\mathrm{CF}$ が点 $\mathrm{P}$ で交わることがわかります。

解答

ア：2
イ：3

解答編　つづき

問題

(2) 五面体において、面 $\mathrm{ABC}$ は一辺の長さが $3$ の正三角形であり、\[ \mathrm{AD=7,\ BE=11,\ CF=17,\ DE=9} \]であるとする。また、6点 $\mathrm{A,B,C,D,E,F}$ はある一つの球面上にあるとし、その球面を $\mathrm{S}$ とする。直線 $\mathrm{AD}$ と $\mathrm{BE}$ の交点を $\mathrm{P}$ とする。

(i) 平面 $\mathrm{ABED}$ と球面 $S$ が交わる部分は円であり、4点 $\mathrm{A,B,E,D}$ はその円周上にある。このことから、三角形 $\mathrm{PAB}$ と $\mathrm{PED}$ は相似であることがわかり、その相似比は $1:\myBox{ウ}$ である。したがって
\begin{eqnarray} \mybox{ウ} \mathrm{PA} &=& \mathrm{PB}+\myBox{エオ} \\[5pt] \mybox{ウ} \mathrm{PB} &=& \mathrm{PA}+\myBox{カ} \\[5pt] \end{eqnarray} が成り立つ。よって\[ \mathrm{PA}=\myBox{キ},\ \mathrm{PB}=\myBox{ク} \]となる。

解説

(2)
(i)

球を平面で切ると、必ず切り口は円になります。球面 $S$ と平面 $\mathrm{ABED}$ とが交わる部分は円になり、4点 $\mathrm{A,B,E,D}$ はこの円周上にあります。 $\mathrm{P}$ は同じ平面上にあります。

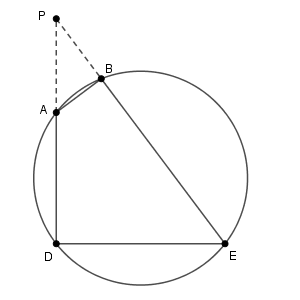
このことから、三角形 $\mathrm{PAB}$ と三角形 $\mathrm{PED}$ は相似であり、相似比は\[ \mathrm{AB}:\mathrm{ED}=3:9=1:3 \]です。よって、
\begin{eqnarray} 3\mathrm{PA} &=& \mathrm{PE} \\[5pt] &=& \mathrm{PB}+\mathrm{BE} \\[5pt] &=& \mathrm{PB}+11 \\[5pt] \end{eqnarray}と \begin{eqnarray} 3\mathrm{PB} &=& \mathrm{PD} \\[5pt] &=& \mathrm{PA}+\mathrm{AD} \\[5pt] &=& \mathrm{PA}+7 \\[5pt] \end{eqnarray}が成り立ちます。2つ目を1つ目に代入して \begin{eqnarray} 3\mathrm{PA} &=& \mathrm{PB}+11 \\[5pt] 3\mathrm{PA} &=& \frac{1}{3}(\mathrm{PA}+7)+11 \\[5pt] \frac{8}{3}\mathrm{PA} &=& \frac{40}{3} \\[5pt] \mathrm{PA} &=& 5 \\[5pt] \end{eqnarray}が得られ、これを2つ目に代入して \begin{eqnarray} 3\mathrm{PB} &=& \mathrm{PA}+7 \\[5pt] 3\mathrm{PB} &=& 5+7 \\[5pt] \mathrm{PB} &=& 4 \\[5pt] \end{eqnarray}と求められます。

解答

ウ：3
エオカ：117
ク：3
キク：54

解答編　つづき

問題

(ii) 平面 $\mathrm{BCFE}$ と球面 $S$ が交わる部分に着目すると、方べきの定理より\[ \mathrm{PC}=\myBox{ケ} \]となる。したがって\[ \mathrm{EF}=\myBox{コサ},\ \mathrm{DF}=\myBox{シス} \]となる。

解説

(2)
(ii)

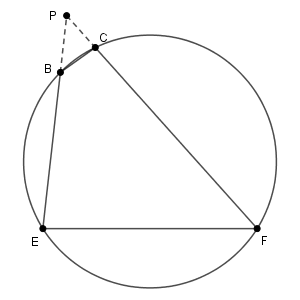
方べきの定理より
\begin{eqnarray} \mathrm{PB}\cdot\mathrm{PE} &=& \mathrm{PC}\cdot\mathrm{PF} \\[5pt] 4\cdot(4+11) &=& \mathrm{PC}\cdot (\mathrm{PC}+17) \\[5pt] 60 &=& \mathrm{PC}^2+17\mathrm{PC} \\[5pt] \mathrm{PC}^2+17\mathrm{PC}-60 &=& 0 \\[5pt] (\mathrm{PC}+20)(\mathrm{PC}-3) &=& 0 \\[5pt] \end{eqnarray}$\mathrm{PC}$ は正なので、 $\mathrm{PC}=3$ と求められます。

これより、
\begin{eqnarray} \mathrm{BC}:\mathrm{FE} &=& \mathrm{PB}:\mathrm{PF} \\[5pt] 3:\mathrm{EF} &=& 4:(3+17) \\[5pt] \mathrm{EF} &=& 15 \end{eqnarray}となります。平面 $\mathrm{ACFD}$ と球面 $S$ についても同様に方べきの定理を使うと \begin{eqnarray} \mathrm{AC}:\mathrm{FD} &=& \mathrm{PC}:\mathrm{PD} \\[5pt] 3:\mathrm{DF} &=& 3:(5+7) \\[5pt] \mathrm{DF} &=& 12 \end{eqnarray}となることがわかります。

解答

ケ：3
コサ：15
シス：12

解答編　つづき

問題

(iii) $\angle\mathrm{ADE}, \angle\mathrm{ADF}, \angle\mathrm{EDF}$ の大きさに着目すると、次の命題(a), (b), (c) の真偽の組合せとして正しいものは $\dBox{セ}$ であることがわかる。

　(a) 平面 $\mathrm{ABED}$ と平面 $\mathrm{DEF}$ は垂直である。
　(b) 直線 $\mathrm{DE}$ は平面 $\mathrm{ACFD}$ に垂直である。
　(c) 直線 $\mathrm{AC}$ と直線 $\mathrm{DE}$ は垂直である。

$\dbox{セ}$ の解答群

　0: (a)真　(b)真　(c)真
　1: (a)真　(b)真　(c)偽
　2: (a)真　(b)偽　(c)真
　3: (a)真　(b)偽　(c)偽
　4: (a)偽　(b)真　(c)真
　5: (a)偽　(b)真　(c)偽
　6: (a)偽　(b)偽　(c)真
　7: (a)偽　(b)偽　(c)偽

解説

(2)
(iii)

いろいろな長さを求めたので、角度について考えます。

$\angle \mathrm{ADE}$ に注目します。三角形 $\mathrm{PDE}$ は、辺の長さが $9,12,15$ 、つまり、 $3:4:5$ なので、直角三角形です。 $\mathrm{PD}\perp\mathrm{DE}$ が成り立ちます。

$\angle \mathrm{ADF}$ に注目します。三角形 $\mathrm{PDF}$ は、辺の長さが $12,12,20$ なので、直角三角形ではないことがわかります。 $\mathrm{PD}$ と $\mathrm{DF}$ は垂直ではありません。

$\angle \mathrm{EDF}$ に注目します。三角形 $\mathrm{DEF}$ は、辺の長さが $9,12,15$ 、つまり、 $3:4:5$ なので、直角三角形です。 $\mathrm{DE}\perp\mathrm{DF}$ が成り立ちます。

イメージとしては、辺の長さが $9,12,15$ の直角三角形を用意し（三角形 $\mathrm{DEF}$ と考えます）、 $\mathrm{DE}$ を中心に回転させ、90度よりも小さいところで止めて $\mathrm{F}$ が $\mathrm{P}$ にうつるようにした、という状況になっています。

これらを踏まえて考えます。

$\mathrm{PD}\perp\mathrm{DE}$ と $\mathrm{DE}\perp\mathrm{DF}$ から、直線 $\mathrm{DE}$ は3点 $\mathrm{P,D,F}$ を含む平面、つまり、平面 $\mathrm{ACFD}$ と垂直であることがわかります。

また、これより、直線 $\mathrm{DE}$ は平面 $\mathrm{ACFD}$ 上の直線と垂直なので、直線 $\mathrm{AC}$ と直線 $\mathrm{DE}$ は垂直です。

$\mathrm{PD}\perp\mathrm{DE}$ と $\mathrm{DE}\perp\mathrm{DF}$ から、平面 $\mathrm{ABED}$ と平面 $\mathrm{DEF}$ のなす角は $\angle\mathrm{ADF}$ と一致します。直角ではないので、平面 $\mathrm{ABED}$ と平面 $\mathrm{DEF}$ は垂直でないことがわかります。

以上から、選択肢の中からは、誤、正、正 の4が正解だとわかります。

解答

セ：4