共通テスト 数学I・数学A 2025年度 第2問 [2] 解説
【必答問題】
問題編
問題
以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。
「(第1四分位数)-1.5×(四分位範囲)」以下の値
「(第3四分位数)+1.5×(四分位範囲)」以上の値太郎さんは、47都道府県における外国人宿泊者数と日本人宿泊者数の動向を調べるため、それらに関するデータを分析することにした。外国人宿泊者数を、日本国内に住所を有しない宿泊者の人数の1年間の合計とし、日本人宿泊者数を、日本国内に住所を有する宿泊者の人数の1年間の合計とする。宿泊者数に関するデータは千の位を四捨五入し、1万人単位で表したものとし、以下においては単位(万人)を省略して用いることとする。例えば「4567890人」は「457」とする。
なお、以下の図や表については、国土交通省のWebページをもとに作成している。
(1)
(i) 図1 は、47都道府県における令和4年の外国人宿泊者数と日本人宿泊者数の散布図である。なお、散歩図には原点を通り、傾きが 10 の直線(破線)を付加している。また、日本人宿泊者数が 1000 を超える都道府県の数は 12 である。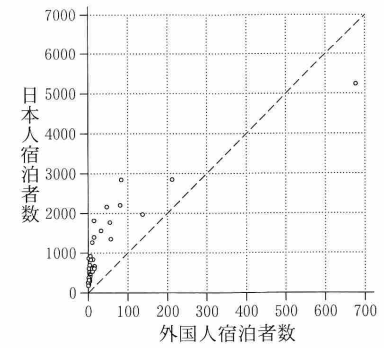
図1 令和4年の外国人宿泊者数と日本人宿泊者数の散布図 次の (a), (b) は、図1に関する記述である。
(a) 令和4年について、外国人宿泊者数が 100 を超え、かつ日本人宿泊者数が 2500 を超える都道府県の数は 2 である。
(b) 令和4年について、日本人宿泊者数が外国人宿泊者数の 10倍未満である都道府県の割合は 50% 未満である。(a), (b) の正誤の組合せとして正しいものは $\dBox{タ}$ である。
$\dbox{タ}$ の解答群
0: (a) 正 (b) 正
1: (a) 正 (b) 誤
2: (a) 誤 (b) 正
3: (a) 誤 (b) 誤(ii) 47都道府県における令和4年の外国人宿泊者数を分析した結果、外れ値となる都道府県の数は 8 であった。
一方、表1 は 47都道府県における令和4年の日本人宿泊者数を、値の小さい順に並べ、その順に都道府県 P1, P2, …, P47 としたものである。この中で、外国人宿泊者数で外れ値となる都道府県(P37, P40, P42, P43, P44, P45, P46, P47) に印 * を付けている。
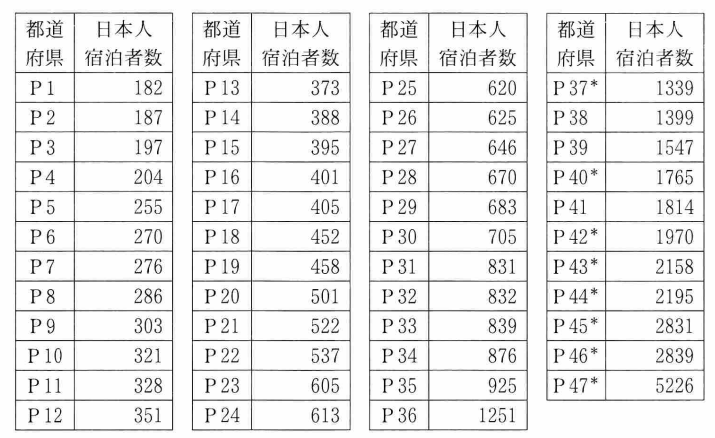
表1 47都道府県における令和4年の日本人宿泊者数 表1のデータにおいて、四分位範囲は $\dBox{チ}$ となることから、令和4年の外国人宿泊者数と日本人宿泊者数の両方で外れ値となる都道府県の数は $\myBox{ツ}$ である。
$\dbox{チ}$ の解答群
0: $320$
1: $450$
2: $597$
3: $638$
4: $900$
5: $966$
6: $1253$
7: $1261$
8: $1602$
9: $1864$(2) 47都道府県におけるある外国人宿泊者数を $x$ 、日本人宿泊者数を $y$ とし、 $x$ と $y$ の値の組を、それぞれ\[ (x_1,y_1),(x_2,y_2),\cdots,(x_{47},y_{47}) \]と表す。 $x,y$ の平均値をそれぞれ $\bar{x},\bar{y}$ とし、 $x,y$ の分散をそれぞれ $s_x^2,s_y^2$ とする。また、 $x$ と $y$ の共分散を $s_{xy}$ とする。
47都道府県それぞれにおける外国人宿泊者数と日本人宿泊者数を足し合わせた合計宿泊者数を $z$ とし、その値を\[ z_i=x_i+y_i \quad(i=1,2,\cdots,47) \]と表す。例えば、 $i=7$ のときは $z_7=x_7+y_7$ である。
$z$ の平均値を $\bar{z}$ とするとき\[ z_i-\bar{z}=(x_i-\bar{x})+(y_i-\bar{y}) \quad(i=1,2,\cdots,47) \]である。このことに着目すると、 $z$ の分散を $s_z^2$ とするとき、 $s_z^2=\dBox{テ}$ となる。
また、令和4年の $x$ と $y$ の間には正の相関があることが図1からわかる。このことから、令和4年について、 $s_z^2$ と $s_x^2+s_y^2$ の関係として、後の 0 ~ 2 のうち、正しいものは $\dBox{ト}$ であることがわかる。

図1(再掲) $\dbox{テ}$ の解答群
0: $s_x^2+s_y^2-2s_{xy}$
1: $s_x^2+s_y^2-s_{xy}$
2: $s_x^2+s_y^2$
3: $s_x^2+s_y^2+s_{xy}$
4: $s_x^2+s_y^2+2s_{xy}$
$\dbox{ト}$ の解答群
0: $s_z^2 \gt s_x^2+s_y^2$
1: $s_z^2 = s_x^2+s_y^2$
2: $s_z^2 \lt s_x^2+s_y^2$
(3) 太郎さんが住む地域では、その地域に宿泊を促すためのキャンペーンとして、キャンペーンA、Bが実施されている。
太郎さんは、キャンペーンAの方がよいと思っている人が多いといううわさを聞いた。このうわさのとおり、キャンペーンAの方がよいと思っている人が多いといえるかどうかを確かめることにした。そこで、かたよりなく選んだ人たちに、キャンペーンA、Bのどちらがよいかについて、二択のアンケートを行ったところ、アンケートに回答した 35人のうち、23人が「キャンペーンAの方がよい」と答えた。この結果から、一般にキャンペーンAの方がよいと思っている人が多いといえるかどうかを、次の方針で考えることにした。
方針
- "「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい" という仮説を立てる。
- この仮説のもとで、かたよりなく選ばれた 35人のうち 23人以上が「キャンペーンAの方がよい」と回答する確率が 5% 未満であれば、その仮説は誤っていると判断し、5% 以上であればその仮説は誤っているとは判断しない。
後の 実験結果 は、35枚の硬貨を投げる実験を 1000回行ったとき、表が出た枚数ごとの回数の割合を示したものである。
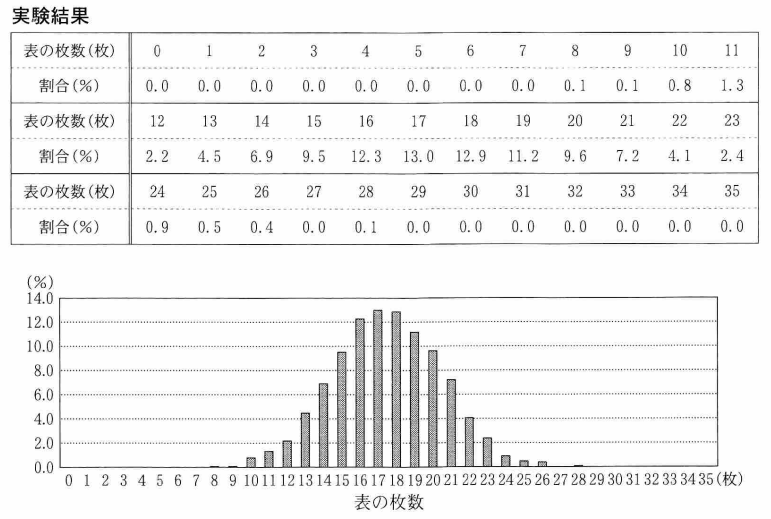
実験結果を用いると、35枚の硬貨のうち 23枚以上が表となった割合は、 $\myBox{ナ}.\ \myBox{ニ}$ %である。これを、35人のうち 23人以上が「キャンペーンAの方がよい」と回答する確率とみなし、方針に従うと、"「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい" という仮説は $\dBox{ヌ}$ 。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が $\dBox{ネ}$ 。
$\dbox{ヌ}$, $\dbox{ネ}$ については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。
$\dbox{ヌ}$ の解答群
0: 誤っていると判断する
1: 誤っているとは判断しない$\dbox{ネ}$ の解答群
0: 多いといえる
1: 多いとはいえない
考え方
新課程で新しく追加された外れ値や仮説検定の部分は、試作問題を見ていれば落ち着いて対応できたでしょう。
散布図内の直線をどう使うか、という問題も過去問ではよく出題されています。事前にどれだけ対策していたかが、結果に反映されるような問題になっています。
【必答問題】
解答編
問題
以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。
「(第1四分位数)-1.5×(四分位範囲)」以下の値
「(第3四分位数)+1.5×(四分位範囲)」以上の値太郎さんは、47都道府県における外国人宿泊者数と日本人宿泊者数の動向を調べるため、それらに関するデータを分析することにした。外国人宿泊者数を、日本国内に住所を有しない宿泊者の人数の1年間の合計とし、日本人宿泊者数を、日本国内に住所を有する宿泊者の人数の1年間の合計とする。宿泊者数に関するデータは千の位を四捨五入し、1万人単位で表したものとし、以下においては単位(万人)を省略して用いることとする。例えば「4567890人」は「457」とする。
なお、以下の図や表については、国土交通省のWebページをもとに作成している。
(1)
(i) 図1 は、47都道府県における令和4年の外国人宿泊者数と日本人宿泊者数の散布図である。なお、散歩図には原点を通り、傾きが 10 の直線(破線)を付加している。また、日本人宿泊者数が 1000 を超える都道府県の数は 12 である。
図1 令和4年の外国人宿泊者数と日本人宿泊者数の散布図 次の (a), (b) は、図1に関する記述である。
(a) 令和4年について、外国人宿泊者数が 100 を超え、かつ日本人宿泊者数が 2500 を超える都道府県の数は 2 である。
(b) 令和4年について、日本人宿泊者数が外国人宿泊者数の 10倍未満である都道府県の割合は 50% 未満である。(a), (b) の正誤の組合せとして正しいものは $\dBox{タ}$ である。
$\dbox{タ}$ の解答群
0: (a) 正 (b) 正
1: (a) 正 (b) 誤
2: (a) 誤 (b) 正
3: (a) 誤 (b) 誤
解説
(1)
(i)
散布図をもとに、一つずつ見ていきます。

(a) について、外国人宿泊者数が100を超えているものは、3点あります。そのうち、日本人宿泊者数が2500を超えているものは2点なので、正しいことがわかります。
ちなみに、問題文に「日本人宿泊者数が1000を超えている都道府県の数は12」とありますが、これは数えてみると確かに12個あるので、「日本人宿泊者数が1000を超えている点は、重なっていませんよ」という意味で書いてあります。
(b) について、破線は
日本人宿泊者数 = 外国人宿泊者数 × 10
の式を表しており、これより上にある点は、日本人宿泊者数のほうがさらに多いことを表しています。なので、「日本人宿泊者数が外国人宿泊者数の10倍未満」とは、破線より下にある点が対応するので、1点しかありません。つまり、50%未満だから、正しいことがわかります。
解答
タ:0(2点)
解答編 つづき
問題
(ii) 47都道府県における令和4年の外国人宿泊者数を分析した結果、外れ値となる都道府県の数は 8 であった。
一方、表1 は 47都道府県における令和4年の日本人宿泊者数を、値の小さい順に並べ、その順に都道府県 P1, P2, …, P47 としたものである。この中で、外国人宿泊者数で外れ値となる都道府県(P37, P40, P42, P43, P44, P45, P46, P47) に印 * を付けている。

表1 47都道府県における令和4年の日本人宿泊者数 表1のデータにおいて、四分位範囲は $\dBox{チ}$ となることから、令和4年の外国人宿泊者数と日本人宿泊者数の両方で外れ値となる都道府県の数は $\myBox{ツ}$ である。
$\dbox{チ}$ の解答群
0: $320$
1: $450$
2: $597$
3: $638$
4: $900$
5: $966$
6: $1253$
7: $1261$
8: $1602$
9: $1864$
解説
(1)
(ii)
四分位範囲は、第三四分位数から第一四分位数を引いて求めます。
第一四分位数は、半分にわけた小さい方の中央値なので、下側23個の中央値、つまり、下から12番目なので、351です。第3四分位数は、大きい方から12番目だから1251です。なので、四分位範囲は\[ 1251-351=900 \]です。選択肢の中では、4です。
問題文の冒頭より、第一四分位数から四分位範囲の1.5倍より以下の値は外れ値とします。この値を計算すると
\begin{eqnarray}
351-1.5\cdot 900 \lt 0
\end{eqnarray}なので、対応する値はないことがわかります。一方、第三四分位数より四分位範囲の1.5倍以上大きい値も外れ値です。この値は
\begin{eqnarray}
1251+1.5\cdot 900 =1251+1350=2501
\end{eqnarray}なので、表の中では、 $\mathrm{P}45$, $\mathrm{P}46$, $\mathrm{P}47$ が該当します。どれも*印がついているので、外国人・日本人どちらも外れ値となるのは、3個あることがわかります。
解答
チ:4(2点)
ト:3(2点)
解答編 つづき
問題
(2) 47都道府県におけるある外国人宿泊者数を $x$ 、日本人宿泊者数を $y$ とし、 $x$ と $y$ の値の組を、それぞれ\[ (x_1,y_1),(x_2,y_2),\cdots,(x_{47},y_{47}) \]と表す。 $x,y$ の平均値をそれぞれ $\bar{x},\bar{y}$ とし、 $x,y$ の分散をそれぞれ $s_x^2,s_y^2$ とする。また、 $x$ と $y$ の共分散を $s_{xy}$ とする。
47都道府県それぞれにおける外国人宿泊者数と日本人宿泊者数を足し合わせた合計宿泊者数を $z$ とし、その値を\[ z_i=x_i+y_i \quad(i=1,2,\cdots,47) \]と表す。例えば、 $i=7$ のときは $z_7=x_7+y_7$ である。
$z$ の平均値を $\bar{z}$ とするとき\[ z_i-\bar{z}=(x_i-\bar{x})+(y_i-\bar{y}) \quad(i=1,2,\cdots,47) \]である。このことに着目すると、 $z$ の分散を $s_z^2$ とするとき、 $s_z^2=\dBox{テ}$ となる。
また、令和4年の $x$ と $y$ の間には正の相関があることが図1からわかる。このことから、令和4年について、 $s_z^2$ と $s_x^2+s_y^2$ の関係として、後の 0 ~ 2 のうち、正しいものは $\dBox{ト}$ であることがわかる。

図1(再掲) $\dbox{テ}$ の解答群
0: $s_x^2+s_y^2-2s_{xy}$
1: $s_x^2+s_y^2-s_{xy}$
2: $s_x^2+s_y^2$
3: $s_x^2+s_y^2+s_{xy}$
4: $s_x^2+s_y^2+2s_{xy}$
$\dbox{ト}$ の解答群
0: $s_z^2 \gt s_x^2+s_y^2$
1: $s_z^2 = s_x^2+s_y^2$
2: $s_z^2 \lt s_x^2+s_y^2$
解説
(2)
$z$ の分散を出すためには\[ z_i-\bar{z} \]を2乗して足し合わせて $47$ で割って求めます。$z_i-\bar{z}$ の2乗は
\begin{eqnarray}
(x_i-\bar{x})^2+2(x_i-\bar{x})(y_i-\bar{y})+(y_i-\bar{y})^2
\end{eqnarray}と展開できます。1項目を $i=1,2,\cdots,47$ として足して $47$ で割ると $s_x^2$ が出てきます。同様に、3項目からは $s_y^2$ が出てきます。2項目を $i=1,2,\cdots,47$ として足して $47$ で割ると $s_{xy}$ が出てくることから\[ s_z^2=s_x^2+2s_{xy}+s_y^2 \]が成り立ちます。
正の相関があることから、共分散 $s_{xy}$ は正なので、\[ s_z^2 \gt s_x^2+s_y^2 \]であることがわかります。
解答
テ:4(3点)
ト:0(2点。ただし、テが正解の場合のみ)
解答編 つづき
問題
(3) 太郎さんが住む地域では、その地域に宿泊を促すためのキャンペーンとして、キャンペーンA、Bが実施されている。
太郎さんは、キャンペーンAの方がよいと思っている人が多いといううわさを聞いた。このうわさのとおり、キャンペーンAの方がよいと思っている人が多いといえるかどうかを確かめることにした。そこで、かたよりなく選んだ人たちに、キャンペーンA、Bのどちらがよいかについて、二択のアンケートを行ったところ、アンケートに回答した 35人のうち、23人が「キャンペーンAの方がよい」と答えた。この結果から、一般にキャンペーンAの方がよいと思っている人が多いといえるかどうかを、次の方針で考えることにした。
方針
- "「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい" という仮説を立てる。
- この仮説のもとで、かたよりなく選ばれた 35人のうち 23人以上が「キャンペーンAの方がよい」と回答する確率が 5% 未満であれば、その仮説は誤っていると判断し、5% 以上であればその仮説は誤っているとは判断しない。
後の 実験結果 は、35枚の硬貨を投げる実験を 1000回行ったとき、表が出た枚数ごとの回数の割合を示したものである。

実験結果を用いると、35枚の硬貨のうち 23枚以上が表となった割合は、 $\myBox{ナ}.\ \myBox{ニ}$ %である。これを、35人のうち 23人以上が「キャンペーンAの方がよい」と回答する確率とみなし、方針に従うと、"「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい" という仮説は $\dBox{ヌ}$ 。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が $\dBox{ネ}$ 。
$\dbox{ヌ}$, $\dbox{ネ}$ については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。
$\dbox{ヌ}$ の解答群
0: 誤っていると判断する
1: 誤っているとは判断しない$\dbox{ネ}$ の解答群
0: 多いといえる
1: 多いとはいえない
解説
(3)
実験結果から、23枚以上が表になった割合は
\begin{eqnarray}
2.4+0.9+0.5+0.4+0.1=4.3
\end{eqnarray}なので、 $4.3$ % だとわかります。
これは $5$ % より小さいので、方針の通りに判断すると、AがいいとBがいいの割合が等しいという仮説は、間違っていると判断するため、キャンペーンAのほうがよいと思っている人が多いといえます。
ちなみに、この問題は、試作問題の仮説検定の部分の問題とほぼ同じです。
解答
ナニ:4300(4点)





