共通テスト 数学I・数学A 2025年度 第1問 [2] 解説

【必答問題】

問題編

問題

　図1のように、直線 $\ell$ 上の点 $\mathrm{A}$ において $\ell$ に接する半径 $2$ の円を円 $\mathrm{O}$ とし、 $\ell$ 上の点 $\mathrm{B}$ において $\ell$ に接する半径 $4$ の円を円 $\mathrm{O'}$ とする。円 $\mathrm{O}$ と $\mathrm{O'}$ は2点で交わるとし、その交点を $\mathrm{P,Q}$ とする。ただし、 $\angle\mathrm{APB}\lt\angle\mathrm{AQB}$ とする。さらに、 $\angle\mathrm{PAB}$ は鋭角であるとする。このとき、 $\triangle\mathrm{PAB}$ と $\triangle\mathrm{QAB}$ について考えよう。

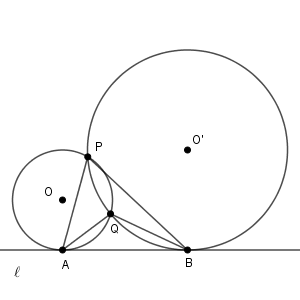
(1) $\angle\mathrm{PAB}=\alpha$, $\angle\mathrm{PBA}=\beta$ とおく。

　円 $\mathrm{O}$ の中心 $\mathrm{O}$ から直線 $\mathrm{PA}$ に引いた垂線と直線 $\mathrm{PA}$ との交点を $\mathrm{H}$ とする。 $\angle\mathrm{OAB}=90^{\circ}$ であるから、 $\angle\mathrm{AOH}=\alpha$ である。よって、 $\triangle\mathrm{OAH}$ に着目すると、 $\mathrm{AH}=\myBox{コ}\sin\alpha$ であるから\[ \mathrm{PA}=2\mathrm{AH}=\myBox{サ}\sin\alpha \quad\cdots ① \]である。

　同様にして、円 $\mathrm{O'}$ の中心 $\mathrm{O'}$ から直線 $\mathrm{PB}$ に引いた垂線と直線 $\mathrm{PB}$ との交点を $\mathrm{H'}$ とすると\[ \mathrm{PB}=2\mathrm{BH'}=\myBox{シ}\sin\beta \quad\cdots ② \]であることもわかる。

　また、 $\triangle\mathrm{PAB}$ の外接円の半径を $R_1$ とおくと、正弦定理により\[ \frac{\mathrm{PA}}{\sin\dBox{ス}} = \frac{\mathrm{PB}}{\sin\dBox{セ}} =2R_1 \]が成り立つので\[ \mathrm{PA}\sin\dbox{セ} = \mathrm{PB}\sin\dbox{ス} \]である。この式に、① と ② を代入することにより
\begin{eqnarray} & & \sin\dbox{セ}=\sqrt{\myBox{ソ}}\sin\dbox{ス} \\[5pt] & & \mathrm{PB}=\sqrt{\mybox{ソ}} \mathrm{PA} \end{eqnarray}となることがわかる。さらに\[ R_1=\myBox{タ}\sqrt{\myBox{チ}} \]が得られる。

$\dbox{ス},\ \dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\alpha$
　1: $\beta$

(2) 太郎さんと花子さんは、(1)の考察を振り返っている。

• $\triangle\mathrm{QAB}$ の外接円の半径も求められるかな。
• (1)の $R_1$ の求め方を参考にすればよさそうだね。

　$\triangle\mathrm{PAB}$, $\triangle\mathrm{QAB}$ の外接円の半径をそれぞれ $R_1,R_2$ とおく。このとき、 $R_1\ \dBox{ツ}\ R_2$ である。さらに、 $\sin\angle\mathrm{APB}\ \dBox{テ}\ \sin\angle\mathrm{AQB}$ であることもわかる。

$\dbox{ツ},\ \dbox{テ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\lt$
　1: $=$
　2: $\gt$

(3) 太郎さんと花子さんは、これまでの考察をもとに、 $\triangle\mathrm{PAB}$ と $\triangle\mathrm{QAB}$ の辺の長さについて考えている。

• $\mathrm{AB}$ の長さが与えられれば、 $\mathrm{PA}$ と $\mathrm{QA}$ の長さが求められそうだね。
• $\angle\mathrm{APB}\lt\angle\mathrm{AQB}$ に注意して求めてみようよ。

　$\mathrm{AB}=2\sqrt{7}$ とする。このとき\[ \sin\angle\mathrm{APB}=\frac{\sqrt{\myBox{トナ}}}{\myBox{ニ}} \]である。(1)より、 $\mathrm{PB}=\sqrt{\mybox{ソ}}\mathrm{PA}$ であるから\[ \mathrm{PA}=\sqrt{\myBox{ヌネ}} \]である。

　同様に、 $\mathrm{QA}=\sqrt{7}$ であることがわかる。

考え方

似たような関係式がたくさん出てくるので、どれを使うのか迷ってしまうかもしれません。まず、タチのところでは、どう組み合わせればいいか、試行錯誤しましょう。

(2)は(1)の流れを踏まえて考えます。最後のヌネは何を使うのか少し思いつきにくいですが、三角比の分野でよく使う公式を思い出しましょう。

【必答問題】

解答編

問題

　図1のように、直線 $\ell$ 上の点 $\mathrm{A}$ において $\ell$ に接する半径 $2$ の円を円 $\mathrm{O}$ とし、 $\ell$ 上の点 $\mathrm{B}$ において $\ell$ に接する半径 $4$ の円を円 $\mathrm{O'}$ とする。円 $\mathrm{O}$ と $\mathrm{O'}$ は2点で交わるとし、その交点を $\mathrm{P,Q}$ とする。ただし、 $\angle\mathrm{APB}\lt\angle\mathrm{AQB}$ とする。さらに、 $\angle\mathrm{PAB}$ は鋭角であるとする。このとき、 $\triangle\mathrm{PAB}$ と $\triangle\mathrm{QAB}$ について考えよう。

(1) $\angle\mathrm{PAB}=\alpha$, $\angle\mathrm{PBA}=\beta$ とおく。

　円 $\mathrm{O}$ の中心 $\mathrm{O}$ から直線 $\mathrm{PA}$ に引いた垂線と直線 $\mathrm{PA}$ との交点を $\mathrm{H}$ とする。 $\angle\mathrm{OAB}=90^{\circ}$ であるから、 $\angle\mathrm{AOH}=\alpha$ である。よって、 $\triangle\mathrm{OAH}$ に着目すると、 $\mathrm{AH}=\myBox{コ}\sin\alpha$ であるから\[ \mathrm{PA}=2\mathrm{AH}=\myBox{サ}\sin\alpha \quad\cdots ① \]である。

　同様にして、円 $\mathrm{O'}$ の中心 $\mathrm{O'}$ から直線 $\mathrm{PB}$ に引いた垂線と直線 $\mathrm{PB}$ との交点を $\mathrm{H'}$ とすると\[ \mathrm{PB}=2\mathrm{BH'}=\myBox{シ}\sin\beta \quad\cdots ② \]であることもわかる。

解説

(1)
$\angle\mathrm{PAB}$ も $\angle\mathrm{AOH}$ も、 $90^{\circ}-\angle\mathrm{OAH}$ と表せます。

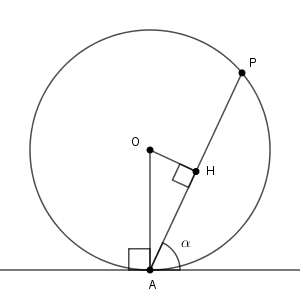
なので、 $\angle\mathrm{AOH}=\angle\mathrm{PAB}=\alpha$ となります。 $\triangle \mathrm{OAH}$ に注目すると、 \[ \mathrm{AH}=\mathrm{OA}\sin\angle\mathrm{AOH} =2\sin\alpha \]となります。なので、
\begin{eqnarray} \mathrm{PA}=2\mathrm{AH}=4\sin\alpha \end{eqnarray}となります。

同じように考えれば、 $\angle\mathrm{BO'H'}=\angle\mathrm{PBA}=\beta$ となり、 $\mathrm{BH'}=4\sin\beta$ だとわかるので、
\begin{eqnarray} \mathrm{PB}=2\mathrm{BH'}=8\sin\beta \end{eqnarray}となります。

解答

コサ：24
シ：8

解答編　つづき

問題

　また、 $\triangle\mathrm{PAB}$ の外接円の半径を $R_1$ とおくと、正弦定理により\[ \frac{\mathrm{PA}}{\sin\dBox{ス}} = \frac{\mathrm{PB}}{\sin\dBox{セ}} =2R_1 \]が成り立つので\[ \mathrm{PA}\sin\dbox{セ} = \mathrm{PB}\sin\dbox{ス} \]である。この式に、① と ② を代入することにより
\begin{eqnarray} & & \sin\dbox{セ}=\sqrt{\myBox{ソ}}\sin\dbox{ス} \\[5pt] & & \mathrm{PB}=\sqrt{\mybox{ソ}} \mathrm{PA} \end{eqnarray}となることがわかる。さらに\[ R_1=\myBox{タ}\sqrt{\myBox{チ}} \]が得られる。

$\dbox{ス},\ \dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\alpha$
　1: $\beta$

解説

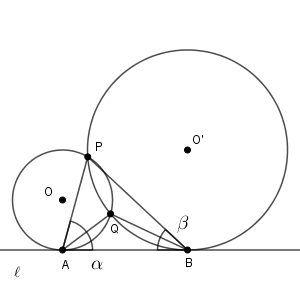
正弦定理をそのまま使えば
\begin{eqnarray} \frac{\mathrm{PA}}{\sin\beta}=\frac{\mathrm{PB}}{\sin\alpha}=2R_1 \end{eqnarray}が成り立つことがわかります。これより、\[ \mathrm{PA}\sin\alpha=\mathrm{PB}\sin\beta\]が成り立ちます。サ・シの内容を代入すると \begin{eqnarray} 4\sin\alpha \sin\alpha &=& 8\sin\beta\sin\beta \\[5pt] \sin^2\alpha &=& 2\sin^2\beta \\[5pt] \sin\alpha &=& \sqrt{2}\sin\beta \\[5pt] \end{eqnarray}となることがわかります。（$\sin\alpha,\sin\beta$ が $0$ 以上であることも使っています。）

また、次のようにも表せます。
\begin{eqnarray} \mathrm{PA}\sin\alpha &=& \mathrm{PB}\sin\beta \\[5pt] \mathrm{PA}\cdot \sqrt{2}\sin\beta &=& \mathrm{PB}\sin\beta \\[5pt] \mathrm{PB} &=& \sqrt{2}\mathrm{PA} \\[5pt] \end{eqnarray}

サより、 $\mathrm{PA}=4\sin\alpha$ で、先ほど求めたように $\sin\alpha=\sqrt{2}\sin\beta$ なので、正弦定理の式に代入すると
\begin{eqnarray} \frac{\mathrm{PA}}{\sin\beta}&=& 2R_1 \\[5pt] \frac{4\sin\alpha}{\sin\beta}&=& 2R_1 \\[5pt] \frac{4\sqrt{2}\sin\beta}{\sin\beta}&=& 2R_1 \\[5pt] 4\sqrt{2} &=& 2R_1 \\[5pt] R_1 &=& 2\sqrt{2} \\[5pt] \end{eqnarray}と求められます。

解答

スセ：10
ソ：2
タチ：22

解答編　つづき

問題

(2) 太郎さんと花子さんは、(1)の考察を振り返っている。

• $\triangle\mathrm{QAB}$ の外接円の半径も求められるかな。
• (1)の $R_1$ の求め方を参考にすればよさそうだね。

　$\triangle\mathrm{PAB}$, $\triangle\mathrm{QAB}$ の外接円の半径をそれぞれ $R_1,R_2$ とおく。このとき、 $R_1\ \dBox{ツ}\ R_2$ である。さらに、 $\sin\angle\mathrm{APB}\ \dBox{テ}\ \sin\angle\mathrm{AQB}$ であることもわかる。

$\dbox{ツ},\ \dbox{テ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\lt$
　1: $=$
　2: $\gt$

解説

(2)

(1)と同じようにすると、
\begin{eqnarray} \mathrm{QA} &=& 4\sin\angle\mathrm{QAB} \\[5pt] \mathrm{QB} &=& 8\sin\angle\mathrm{QBA} \\[5pt] \end{eqnarray}がわかります。また、 \begin{eqnarray} \sin\angle\mathrm{QAB} &=& \sqrt{2}\sin\angle\mathrm{QBA} \\[5pt] \mathrm{QB} &=& \sqrt{2}\mathrm{QA} \\[5pt] \end{eqnarray}も得られて、同じように計算して\[ R_2=2\sqrt{2} \]となることがわかります。つまり、\[ R_1=R_2 \]が成り立ちます。

また、正弦定理より、 $\mathrm{AB}$ は、 $R_1\sin\angle\mathrm{APB}$ とも $R_2\sin\angle\mathrm{AQB}$ とも書けます。 $R_1=R_2$ より、 $\sin\angle\mathrm{APB}=\sin\angle\mathrm{AQB}$ であることがわかります。

解答

ツテ：11

解答編　つづき

問題

(3) 太郎さんと花子さんは、これまでの考察をもとに、 $\triangle\mathrm{PAB}$ と $\triangle\mathrm{QAB}$ の辺の長さについて考えている。

• $\mathrm{AB}$ の長さが与えられれば、 $\mathrm{PA}$ と $\mathrm{QA}$ の長さが求められそうだね。
• $\angle\mathrm{APB}\lt\angle\mathrm{AQB}$ に注意して求めてみようよ。

　$\mathrm{AB}=2\sqrt{7}$ とする。このとき\[ \sin\angle\mathrm{APB}=\frac{\sqrt{\myBox{トナ}}}{\myBox{ニ}} \]である。(1)より、 $\mathrm{PB}=\sqrt{\mybox{ソ}}\mathrm{PA}$ であるから\[ \mathrm{PA}=\sqrt{\myBox{ヌネ}} \]である。

　同様に、 $\mathrm{QA}=\sqrt{7}$ であることがわかる。

解説

(3)
$\mathrm{AB}=2\sqrt{7}$ とすると、正弦定理から
\begin{eqnarray} \frac{\mathrm{AB}}{\sin\angle\mathrm{APB}} &=& 2\cdot 2\sqrt{2} \\[5pt] \frac{2\sqrt{7}}{\sin\angle\mathrm{APB}} &=& 4\sqrt{2} \\[5pt] \frac{2\sqrt{7}}{4\sqrt{2}} &=& \sin\angle\mathrm{APB} \\[5pt] \sin\angle\mathrm{APB} &=& \frac{\sqrt{14}}{4} \\[5pt] \end{eqnarray}となることがわかります。

相互関係より、
\begin{eqnarray} \cos^2\angle\mathrm{APB}=1-\frac{14}{16}=\frac{2}{16} \end{eqnarray}となります。 $\angle\mathrm{APB}$ は鋭角なので、\[ \cos\angle\mathrm{APB}=\frac{\sqrt{2}}{4} \]となります。

ここで、 $\mathrm{PA}=x$ とすると、 $\mathrm{PB}=\sqrt{2}x$ です。余弦定理より
\begin{eqnarray} \cos\angle\mathrm{APB} &=& \frac{\mathrm{PA}^2+\mathrm{PB}^2-\mathrm{AB}^2}{2\mathrm{PA}\cdot\mathrm{PB}} \\[5pt] \frac{\sqrt{2}}{4} &=& \frac{x^2+2x^2-28}{2x\cdot\sqrt{2}x} \\[5pt] \frac{\sqrt{2}}{4} &=& \frac{3x^2-28}{2\sqrt{2}x^2} \\[5pt] \sqrt{2}\cdot 2\sqrt{2}x^2 &=& 4(3x^2-28) \\[5pt] 4x^2 &=& 12x^2-112 \\[5pt] 8x^2 &=& 112 \\[5pt] x^2 &=& 14 \\[5pt] \end{eqnarray}となるので、 $x=\sqrt{14}$ となります。

ちなみに、 $\mathrm{QA}$ の方は、 $\cos$ が負なので、上の計算の途中からは次のようになります。
\begin{eqnarray} -\frac{\sqrt{2}}{4} &=& \frac{3x^2-28}{2\sqrt{2}x^2} \\[5pt] -\sqrt{2}\cdot 2\sqrt{2}x^2 &=& 4(3x^2-28) \\[5pt] -4x^2 &=& 12x^2-112 \\[5pt] 16x^2 &=& 112 \\[5pt] x^2 &=& 7 \\[5pt] \end{eqnarray}こうして、 $\mathrm{QA}=\sqrt{7}$ となり、問題文の通りとなります。

解答

トナニ：144
ヌネ：14