共通テスト 数学I・数学A 2023年度追試 第5問 解説

【第3問～第5問から2問選択】

問題編

問題

　$\triangle \mathrm{ABC}$ において辺 $\mathrm{AB}$ を $2:3$ に内分する点を $\mathrm{P}$ とする。辺 $\mathrm{AC}$ 上に2点 $\mathrm{A,C}$ のいずれとも異なる点 $\mathrm{Q}$ をとる。線分 $\mathrm{BQ}$ と線分 $\mathrm{CP}$ との交点を $\mathrm{R}$ とし、直線 $\mathrm{AR}$ と辺 $\mathrm{BC}$ との交点を $\mathrm{S}$ とする。

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) 点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $1:2$ に内分する点とする。このとき、点 $\mathrm{S}$ は辺 $\mathrm{BC}$ を $\myBox{ア}\ : \ \myBox{イ}$ に内分する点である。

　$\mathrm{AB}=5$ とし、 $\triangle \mathrm{ABC}$ の内接円が辺 $\mathrm{AB}$, 辺 $\mathrm{AC}$ とそれぞれ点 $\mathrm{P}$, 点 $\mathrm{Q}$ で接しているとする。 $\mathrm{AQ}=\myBox{ウ}$ であることに注意すると、 $\mathrm{BC}=\myBox{エ}$ であり、 $\dBox{オ}$ であることがわかる。

$\dbox{オ}$ の解答群

　0: 点 $\mathrm{R}$ は $\triangle \mathrm{ABC}$ の内心
　1: 点 $\mathrm{R}$ は $\triangle \mathrm{ABC}$ の重心
　2: 点 $\mathrm{S}$ は $\triangle \mathrm{ABC}$ の内接円と辺 $\mathrm{BC}$ との接点
　3: 点 $\mathrm{S}$ は点 $\mathrm{A}$ から辺 $\mathrm{BC}$ に下した垂線と辺 $\mathrm{BC}$ との交点

(2) $\triangle \mathrm{BPR}$ と $\triangle \mathrm{CQR}$ の面積比について考察する。

(i) 点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $1:4$ に内分する点とする。このとき、点 $\mathrm{R}$ は、線分 $\mathrm{BQ}$ を $\myBox{カキ}\ : \ \myBox{ク}$ に内分し、線分 $\mathrm{CP}$ を $\myBox{ケコ}\ : \ \myBox{サ}$ に内分する。

　したがって\[ \frac{\triangle \mathrm{CQR}\ \textsf{の面積}}{\triangle \mathrm{BPR}\ \textsf{の面積}} = \frac{\myBox{シス}}{\myBox{セ}} \]である。

(ii) $\dfrac{\triangle \mathrm{CQR}\ \textsf{の面積}}{\triangle \mathrm{BPR}\ \textsf{の面積}} = \dfrac{1}{4}$ のとき、点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $\myBox{ソ}\ : \ \myBox{タ}$ に内分する点である。

考え方

どの条件が生きたままになっているかに注意しながら考えていきましょう。(2)の(ii)は、(i)の応用ですが、自分で応用しないといけない部分が多いので、少し大変です。

解答編

問題

　$\triangle \mathrm{ABC}$ において辺 $\mathrm{AB}$ を $2:3$ に内分する点を $\mathrm{P}$ とする。辺 $\mathrm{AC}$ 上に2点 $\mathrm{A,C}$ のいずれとも異なる点 $\mathrm{Q}$ をとる。線分 $\mathrm{BQ}$ と線分 $\mathrm{CP}$ との交点を $\mathrm{R}$ とし、直線 $\mathrm{AR}$ と辺 $\mathrm{BC}$ との交点を $\mathrm{S}$ とする。

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) 点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $1:2$ に内分する点とする。このとき、点 $\mathrm{S}$ は辺 $\mathrm{BC}$ を $\myBox{ア}\ : \ \myBox{イ}$ に内分する点である。

解説

図は次のようになっています。

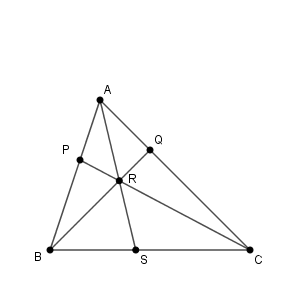
チェバの定理から
\begin{eqnarray} \frac{\mathrm{AP}}{\mathrm{PB}}\cdot\frac{\mathrm{BS}}{\mathrm{SC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}} &=& 1 \\[5pt] \frac{2}{3}\cdot\frac{\mathrm{BS}}{\mathrm{SC}}\cdot\frac{2}{1} &=& 1 \\[5pt] \frac{\mathrm{BS}}{\mathrm{SC}} &=& \frac{3}{4} \\[5pt] \end{eqnarray}となるので、点 $\mathrm{S}$ は辺 $\mathrm{BC}$ を $3:4$ に内分する点だとわかります。

解答

アイ：34 (2点)

解答編　つづき

問題

　$\mathrm{AB}=5$ とし、 $\triangle \mathrm{ABC}$ の内接円が辺 $\mathrm{AB}$, 辺 $\mathrm{AC}$ とそれぞれ点 $\mathrm{P}$, 点 $\mathrm{Q}$ で接しているとする。 $\mathrm{AQ}=\myBox{ウ}$ であることに注意すると、 $\mathrm{BC}=\myBox{エ}$ であり、 $\dBox{オ}$ であることがわかる。

$\dbox{オ}$ の解答群

　0: 点 $\mathrm{R}$ は $\triangle \mathrm{ABC}$ の内心
　1: 点 $\mathrm{R}$ は $\triangle \mathrm{ABC}$ の重心
　2: 点 $\mathrm{S}$ は $\triangle \mathrm{ABC}$ の内接円と辺 $\mathrm{BC}$ との接点
　3: 点 $\mathrm{S}$ は点 $\mathrm{A}$ から辺 $\mathrm{BC}$ に下した垂線と辺 $\mathrm{BC}$ との交点

解説

同じように図をかくと次のようになります。

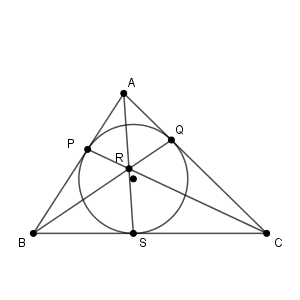
点 $\mathrm{P,Q}$ は内接円と辺との接点なので、 $\mathrm{AP=AQ}$ なので、 $\mathrm{AQ}=2$ とわかります。

これより、 $\mathrm{CQ}=4$ とわかり、
\begin{eqnarray} \mathrm{BC} &=& \mathrm{BP}+\mathrm{CQ} \\[5pt] &=& 3+4=7 \\[5pt] \end{eqnarray}と求められます。 $\mathrm{BS:SC}=3:4$ なので、 $\mathrm{BS=BP}$ がわかるので、点 $\mathrm{S}$ は $\triangle \mathrm{ABC}$ の内接円と辺 $\mathrm{BC}$ との接点であることがわかります。

解答

ウ：2 (2点)
エ：7 (3点)
オ：2 (3点)

解答編　つづき

問題

(2) $\triangle \mathrm{BPR}$ と $\triangle \mathrm{CQR}$ の面積比について考察する。

(i) 点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $1:4$ に内分する点とする。このとき、点 $\mathrm{R}$ は、線分 $\mathrm{BQ}$ を $\myBox{カキ}\ : \ \myBox{ク}$ に内分し、線分 $\mathrm{CP}$ を $\myBox{ケコ}\ : \ \myBox{サ}$ に内分する。

解説

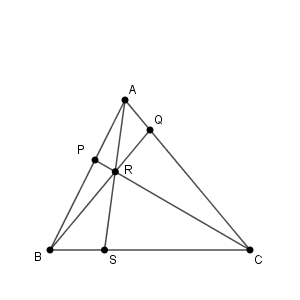
三角形 $\mathrm{ABQ}$ と直線 $\mathrm{CP}$ についてメネラウスの定理を使うと、
\begin{eqnarray} \frac{\mathrm{AP}}{\mathrm{PB}}\cdot\frac{\mathrm{BR}}{\mathrm{RQ}}\cdot\frac{\mathrm{QC}}{\mathrm{CA}} &=& 1 \\[5pt] \frac{2}{3}\cdot\frac{\mathrm{BR}}{\mathrm{RQ}}\cdot\frac{4}{5} &=& 1 \\[5pt] \frac{\mathrm{BR}}{\mathrm{RQ}} &=& \frac{15}{8} \\[5pt] \end{eqnarray}となるので、点 $\mathrm{R}$ は辺 $\mathrm{BQ}$ を $15:8$ に内分する点だとわかります。

三角形 $\mathrm{ACP}$ と直線 $\mathrm{BQ}$ についてメネラウスの定理を使うと、
\begin{eqnarray} \frac{\mathrm{AQ}}{\mathrm{QC}}\cdot\frac{\mathrm{CR}}{\mathrm{RP}}\cdot\frac{\mathrm{PB}}{\mathrm{BA}} &=& 1 \\[5pt] \frac{1}{4}\cdot\frac{\mathrm{CR}}{\mathrm{RP}}\cdot\frac{3}{5} &=& 1 \\[5pt] \frac{\mathrm{CR}}{\mathrm{RP}} &=& \frac{20}{3} \\[5pt] \end{eqnarray}となるので、点 $\mathrm{R}$ は辺 $\mathrm{CP}$ を $20:3$ に内分する点だとわかります。

解答

カキク：158 (2点)
ケコサ：203 (2点)

解答編　つづき

問題

　したがって\[ \frac{\triangle \mathrm{CQR}\ \textsf{の面積}}{\triangle \mathrm{BPR}\ \textsf{の面積}} = \frac{\myBox{シス}}{\myBox{セ}} \]である。

解説

$\triangle \mathrm{BCR}$ を中心に考えてみます。この面積を $S$ とおいて考えます。

$\triangle \mathrm{BCR}$ と $\triangle \mathrm{BPR}$ の面積比は、直線 $\mathrm{CP}$ を底辺と考えれば高さが同じなので、底辺の比と一致することがわかります。先ほど求めたように、 $\mathrm{CR:RP}=20:3$ なので、 $\triangle \mathrm{BPR}$ の面積は\[ \frac{3}{20}S \]だとわかります。

$\triangle \mathrm{BCR}$ と $\triangle \mathrm{CQR}$ の面積比は、直線 $\mathrm{BQ}$ を底辺と考えれば高さが同じなので、底辺の比と一致することがわかります。先ほど求めたように、 $\mathrm{BR:RQ}=15:8$ なので、 $\triangle \mathrm{CQR}$ の面積は\[ \frac{8}{15}S \]だとわかります。

以上から、 $\triangle \mathrm{CQR}$ の面積と $\triangle \mathrm{BPR}$ の面積比は
\begin{eqnarray} \frac{8}{15}S:\frac{3}{20}S &=& \frac{8}{3}:\frac{3}{4} \\[5pt] &=& 32:9 \\[5pt] \end{eqnarray}となるので、 $\dfrac{\triangle \mathrm{CQR}\ \textsf{の面積}}{\triangle \mathrm{BPR}\ \textsf{の面積}} = \dfrac{32}{9}$ となることがわかります。

解答

シスセ：329 (3点)

解答編　つづき

問題

(ii) $\dfrac{\triangle \mathrm{CQR}\ \textsf{の面積}}{\triangle \mathrm{BPR}\ \textsf{の面積}} = \dfrac{1}{4}$ のとき、点 $\mathrm{Q}$ は辺 $\mathrm{AC}$ を $\myBox{ソ}\ : \ \myBox{タ}$ に内分する点である。

解説

今度は、面積比がわかっている状態から線分の比を求める問題です。逆に考えていくのは難しそうなので、先ほどの話で、線分の比を文字で置いて考えていくことにしましょう。図は先ほどの内容を使い回しましょう。

$\mathrm{AQ:QC}=1:t$ と置くことにします。すると、メネラウスの定理から、
\begin{eqnarray} \frac{\mathrm{AP}}{\mathrm{PB}}\cdot\frac{\mathrm{BR}}{\mathrm{RQ}}\cdot\frac{\mathrm{QC}}{\mathrm{CA}} &=& 1 \\[5pt] \frac{2}{3}\cdot\frac{\mathrm{BR}}{\mathrm{RQ}}\cdot\frac{t}{t+1} &=& 1 \\[5pt] \frac{\mathrm{BR}}{\mathrm{RQ}} &=& \frac{3(t+1)}{2t} \\[5pt] \end{eqnarray}となります。また、もう一度メネラウスの定理を使って、 \begin{eqnarray} \frac{\mathrm{AQ}}{\mathrm{QC}}\cdot\frac{\mathrm{CR}}{\mathrm{RP}}\cdot\frac{\mathrm{PB}}{\mathrm{BA}} &=& 1 \\[5pt] \frac{1}{t}\cdot\frac{\mathrm{CR}}{\mathrm{RP}}\cdot\frac{3}{5} &=& 1 \\[5pt] \frac{\mathrm{CR}}{\mathrm{RP}} &=& \frac{5t}{3} \\[5pt] \end{eqnarray}となります。

再び、 $\triangle \mathrm{BCR}$ の面積を $S$ とおいて考えます。

$\triangle \mathrm{BCR}$ と $\triangle \mathrm{BPR}$ の面積比は、 $\mathrm{CR:RP}=5t:3$ なので、 $\triangle \mathrm{BPR}$ の面積は\[ \frac{3}{5t}S \]だとわかります。

$\triangle \mathrm{BCR}$ と $\triangle \mathrm{CQR}$ の面積比は、 $\mathrm{BR:RQ}=3(t+1):2t$ なので、 $\triangle \mathrm{CQR}$ の面積は\[ \frac{2t}{3(t+1)}S \]だとわかります。

ここで、 $\triangle \mathrm{CQR}$ と $\triangle \mathrm{BPR}$ の面積比が $1:4$ になる場合、つまり、\[ \frac{2t}{3(t+1)}S : \frac{3}{5t}S=1:4 \]となる場合を考えればいいです。これを解くと
\begin{eqnarray} \frac{3}{5t}S &=& 4\cdot \frac{2t}{3(t+1)}S \\[5pt] 3\cdot 3(t+1) &=& 5t\cdot 8t \\[5pt] 9t+9 &=& 40t^2 \\[5pt] 40t^2-9t-9 &=& 0 \\[5pt] (5t-3)(8t+3) &=& 0 \\[5pt] t &=& \frac{3}{5},-\dfrac{3}{8} \end{eqnarray}となります。 $\mathrm{Q}$ は辺 $\mathrm{AC}$ 上の点なので、 $t=\dfrac{3}{5}$ だとわかります。つまり、\[ \mathrm{AQ:QC}=1:\dfrac{3}{5}=5:3 \]と求められます。

解答

ソタ：53 (3点)