共通テスト数学I・数学A 2023年度追試第1問 [2] 解説

🕒 2023/02/01 🔄 2023/05/01

【必答問題】

問題編

問題

　$\triangle \mathrm{ABC}$ において $\mathrm{BC}=1$ であるとする。 $\sin\angle \mathrm{ABC}$ と $\sin\angle \mathrm{ACB}$ に関する条件が与えられたときの $\triangle \mathrm{ABC}$ の辺、角、面積について考察する。

(1) $\sin\angle \mathrm{ABC}=\dfrac{\sqrt{15}}{4}$ であるとき、 $\cos\angle\mathrm{ABC}=\pm\dfrac{\myBox{サ}}{\myBox{シ}}$ である。

(2) $\sin\angle \mathrm{ABC}=\dfrac{\sqrt{15}}{4}$, $\sin\angle \mathrm{ACB}=\dfrac{\sqrt{15}}{8}$ であるとする。

(i) このとき、 $\mathrm{AC}=\myBox{ス} \mathrm{AB}$ である。

(ii) この条件を満たす三角形は二つあり、その中で面積が大きい方の $\triangle \mathrm{ABC}$ においては、 $\mathrm{AB}=\dfrac{\myBox{セ}}{\myBox{ソ}}$ である。

(3) $\sin\angle \mathrm{ABC}=2\sin\angle \mathrm{ACB}$ を満たす $\triangle \mathrm{ABC}$ のうち、面積 $S$ が最大となるものを求めよう。

　$\sin\angle \mathrm{ABC}=2\sin\angle \mathrm{ACB}$ と $\mathrm{BC}=1$ により\[ \cos\angle \mathrm{ABC}=\dfrac{\myBox{タ}-\myBox{チ}\mathrm{AB}^2}{2 \mathrm{AB}} \]である。 $\triangle \mathrm{ABC}$ の面積 $S$ について調べるために、 $S^2$ を考える。 $\mathrm{AB}^2=x$ とおくと\[ S^2=-\dfrac{\myBox{ツ}}{\myBox{テト}}x^2+\dfrac{\myBox{ナ}}{\myBox{ニ}}x-\dfrac{1}{16} \]と表すことができる。したがって、 $S^2$ が最大となるのは $x=\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ のとき、すなわち $\mathrm{AB}=\dfrac{\sqrt{\myBox{ノ}}}{\myBox{ハ}}$ のときである。 $S\gt 0$ より、このときに面積 $S$ も最大となる。

　また、面積 $S$ が最大となる $\triangle \mathrm{ABC}$ において、 $\angle \mathrm{ABC}$ は $\dBox{ヒ}$ で、 $\angle \mathrm{ACB}$ は $\dBox{フ}$ である。

$\dbox{ヒ}$, $\dbox{フ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 鋭角
　1: 直角
　2: 鈍角

考え方

(2)の面積が大きい方をどう考えるかは少し難しいです。図をかいて考えましょう。

(3)は(2)の計算を踏まえて考えていくといいでしょう。ただ、計算が大変です。三角比の計算にかなり慣れていないと、最後までたどり着けません。

【必答問題】

解答編

問題

　$\triangle \mathrm{ABC}$ において $\mathrm{BC}=1$ であるとする。 $\sin\angle \mathrm{ABC}$ と $\sin\angle \mathrm{ACB}$ に関する条件が与えられたときの $\triangle \mathrm{ABC}$ の辺、角、面積について考察する。

(1) $\sin\angle \mathrm{ABC}=\dfrac{\sqrt{15}}{4}$ であるとき、 $\cos\angle\mathrm{ABC}=\pm\dfrac{\myBox{サ}}{\myBox{シ}}$ である。

解説

相互関係より
\begin{eqnarray} \cos^2\angle \mathrm{ABC} &=& 1-\left(\frac{\sqrt{15}}{4}\right)^2 \\[5pt] &=& \frac{1}{16} \\[5pt] \end{eqnarray}なので、 $\cos\angle \mathrm{ABC}=\pm\dfrac{1}{4}$ です。

解答

サシ：14 (2点)

解答編　つづき

問題

(2) $\sin\angle \mathrm{ABC}=\dfrac{\sqrt{15}}{4}$, $\sin\angle \mathrm{ACB}=\dfrac{\sqrt{15}}{8}$ であるとする。

(i) このとき、 $\mathrm{AC}=\myBox{ス} \mathrm{AB}$ である。

(ii) この条件を満たす三角形は二つあり、その中で面積が大きい方の $\triangle \mathrm{ABC}$ においては、 $\mathrm{AB}=\dfrac{\myBox{セ}}{\myBox{ソ}}$ である。

解説

正弦定理より
\begin{eqnarray} \frac{\mathrm{AC}}{\sin\angle \mathrm{ABC} } &=& \frac{\mathrm{AB}}{\sin\angle \mathrm{ACB} } \\[5pt] \mathrm{AC} \sin\angle \mathrm{ACB} &=& \mathrm{AB} \sin\angle \mathrm{ABC} \\[5pt] \frac{\sqrt{15}}{8}\mathrm{AC} &=& \frac{\sqrt{15}}{4} \mathrm{AB} \\[5pt] \mathrm{AC} &=& 2\mathrm{AB} \\[5pt] \end{eqnarray}となります。

ここで、 $\sin\theta$ の値が $\dfrac{\sqrt{15}}{4}$ になる角と $\dfrac{\sqrt{15}}{8}$ になる角を考えると、次のようになります。

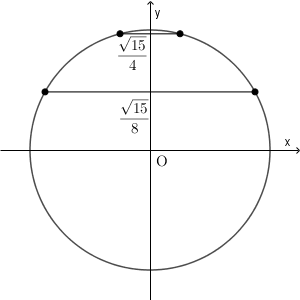
これより、 $\angle \mathrm{ACB}$ が鈍角なら、 $\angle \mathrm{ABC}+\angle \mathrm{ACB}$ が $180^{\circ}$ を超えてしまうことがわかります。なので、 $\angle \mathrm{ACB}$ は鋭角だとわかります。一方、$\angle \mathrm{ABC}$ は鋭角も鈍角もありえます。

$\angle \mathrm{ACB}$ の大きさは決まっているので、 $\angle \mathrm{ABC}$ の大きさによって、三角形は次の二通りがありえることがわかります。

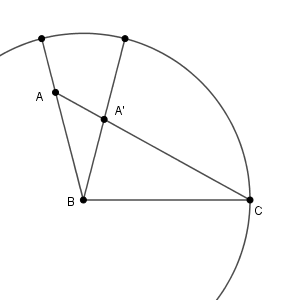
$\mathrm{BC}$ を底辺と考えれば、面積が大きくなるのは高さが大きいときなので、 $\angle \mathrm{ABC}$ が鈍角のときです。このとき、(1)より $\cos\angle \mathrm{ABC}=-\dfrac{1}{4}$ なので、 $\mathrm{AB}=c$ とすると、余弦定理から
\begin{eqnarray} \frac{c^2+1^2-(2c)^2}{2\cdot c\cdot 1} &=& \cos\angle \mathrm{ABC} \\[5pt] \frac{-3c^2+1}{2c} &=& -\frac{1}{4} \\[5pt] -2(-3c^2+1) &=& c \\[5pt] 6c^2-c-2 &=& 0 \\[5pt] (3c-2)(2c+1) &=& 0 \\[5pt] c &=& \frac{2}{3},-\frac{1}{2} \end{eqnarray}となることがわかります。こうして、 $\mathrm{AB}=\dfrac{2}{3}$ と求められます。

解答

ス：2 (3点)
セソ：23 (3点)

解答編　つづき

問題

(3) $\sin\angle \mathrm{ABC}=2\sin\angle \mathrm{ACB}$ を満たす $\triangle \mathrm{ABC}$ のうち、面積 $S$ が最大となるものを求めよう。

　$\sin\angle \mathrm{ABC}=2\sin\angle \mathrm{ACB}$ と $\mathrm{BC}=1$ により\[ \cos\angle \mathrm{ABC}=\dfrac{\myBox{タ}-\myBox{チ}\mathrm{AB}^2}{2 \mathrm{AB}} \]である。 $\triangle \mathrm{ABC}$ の面積 $S$ について調べるために、 $S^2$ を考える。 $\mathrm{AB}^2=x$ とおくと\[ S^2=-\dfrac{\myBox{ツ}}{\myBox{テト}}x^2+\dfrac{\myBox{ナ}}{\myBox{ニ}}x-\dfrac{1}{16} \]と表すことができる。したがって、 $S^2$ が最大となるのは $x=\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ のとき、すなわち $\mathrm{AB}=\dfrac{\sqrt{\myBox{ノ}}}{\myBox{ハ}}$ のときである。 $S\gt 0$ より、このときに面積 $S$ も最大となる。

　また、面積 $S$ が最大となる $\triangle \mathrm{ABC}$ において、 $\angle \mathrm{ABC}$ は $\dBox{ヒ}$ で、 $\angle \mathrm{ACB}$ は $\dBox{フ}$ である。

$\dbox{ヒ}$, $\dbox{フ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 鋭角
　1: 直角
　2: 鈍角

解説

(2)を踏まえて考えます。

正弦定理より、
\begin{eqnarray} \frac{\mathrm{AC}}{\sin\angle \mathrm{ABC} } &=& \frac{\mathrm{AB}}{\sin\angle \mathrm{ACB} } \\[5pt] \mathrm{AC} &=& \mathrm{AB}\cdot \frac{ \sin\angle \mathrm{ABC} }{ \sin\angle \mathrm{ACB} } =2 \mathrm{AB} \\[5pt] \end{eqnarray}となります。

これより、余弦定理から
\begin{eqnarray} \cos\angle \mathrm{ABC} &=& \frac{\mathrm{AB}^2+\mathrm{BC}^2-\mathrm{AC}^2}{2\mathrm{AB}\cdot \mathrm{BC}} \\[5pt] &=& \frac{\mathrm{AB}^2+1-4\mathrm{AB}^2}{2\mathrm{AB}} \\[5pt] &=& \frac{1-3\mathrm{AB}^2}{2\mathrm{AB}} \\[5pt] \end{eqnarray}となります。

$\triangle \mathrm{ABC}$ の面積は\[ \frac{\mathrm{AB}\cdot \mathrm{BC}}{2}\sin\angle \mathrm{ABC}=\frac{\mathrm{AB}}{2}\sin\angle \mathrm{ABC} \]と書けるので、
\begin{eqnarray} S^2 &=& \left( \frac{\mathrm{AB}}{2}\sin\angle \mathrm{ABC} \right)^2 \\[5pt] &=& \frac{\mathrm{AB}^2}{4}\sin^2\angle \mathrm{ABC} \\[5pt] &=& \frac{\mathrm{AB}^2}{4} (1-\cos^2\angle \mathrm{ABC}) \\[5pt] &=& \frac{\mathrm{AB}^2}{4} \left\{1-\left(\frac{1-3\mathrm{AB}^2}{2\mathrm{AB}}\right)^2 \right\} \\[5pt] &=& \frac{\mathrm{AB}^2}{4} \left(1-\frac{1-6\mathrm{AB}^2+9\mathrm{AB}^4}{4\mathrm{AB}^2}\right) \\[5pt] &=& \frac{\mathrm{AB}^2}{4} \cdot \frac{4\mathrm{AB}^2-1+6\mathrm{AB}^2-9\mathrm{AB}^4}{4\mathrm{AB}^2} \\[5pt] &=& \frac{-1+10\mathrm{AB}^2-9\mathrm{AB}^4}{16} \\[5pt] &=& -\frac{9}{16}\mathrm{AB}^4 +\frac{5}{8}\mathrm{AB}^2 -\frac{1}{16} \end{eqnarray}となることがわかります。 $\mathrm{AB}^2=x$ とすると、これは\[ S^2 = -\frac{9}{16}x^2+\frac{5}{8}x-\frac{1}{16} \]とかけて、 $x$ の二次関数で表すことができます。なので、これが最大となる場合は、平方完成をして \begin{eqnarray} & & -\frac{9}{16}x^2+\frac{5}{8}x-\frac{1}{16} \\[5pt] &=& -\frac{9}{16}\left(x^2-\frac{10}{9}x\right)-\frac{1}{16} \\[5pt] &=& -\frac{9}{16}\left(x-\frac{5}{9}\right)^2+\frac{9}{16}\cdot\frac{5^2}{9^2}-\frac{1}{16} \\[5pt] \end{eqnarray}となるので、 $x=\dfrac{5}{9}$ のときに $S^2$ が最大になることがわかります。 $\mathrm{AB}^2=x$ なので、 $\mathrm{AB}=\dfrac{\sqrt{5}}{3}$ のときです。

面積 $S$ が最大となるとき、三辺の長さは
\begin{eqnarray} \mathrm{BC}&=&1 \\[5pt] \mathrm{AB}&=&\frac{\sqrt{5}}{3} \\[5pt] \mathrm{AC}&=&2\mathrm{AB}=\frac{2\sqrt{5}}{3} \\[5pt] \end{eqnarray}となります。2乗して比較すると $\mathrm{AC}$ が一番長いことがわかります。ここで、\[ \mathrm{AB}^2+\mathrm{BC}^2=\frac{14}{9} \lt \mathrm{AC}^2 \]なので、 $\angle \mathrm{ABC}$ は鈍角だとわかります。残りの角は鋭角だから、 $\angle \mathrm{ACB}$ は鋭角です。