共通テスト数学I・数学A 2023年度追試第3問解説

🕒 2023/02/05 🔄 2023/05/01

【第3問～第5問から2問選択】

問題編

問題

(1) 1枚の硬貨を繰り返し投げるとき、この硬貨の表裏の出方に応じて、座標平面上の点 $\mathrm{P}$ が次の規則１に従って移動するものとする。

規則１

点 $\mathrm{P}$ は原点 $\mathrm{O}(0,0)$ を出発点とする。

点 $\mathrm{P}$ の $x$ 座標は、硬貨を投げるごとに $1$ だけ増加する。

点 $\mathrm{P}$ の $y$ 座標は、硬貨を投げるごとに、表が出たら $1$ だけ増加し、裏が出たら $1$ だけ減少する。

　また、点 $\mathrm{P}$ の座標を次の記号で表す。

記号
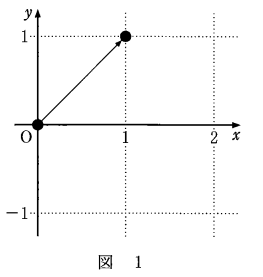
　硬貨を $k$ 回投げ終えた時点での点 $\mathrm{P}$ の座標 $(x,y)$ を $(k,y_k)$ で表す。

　座標平面上の点 $\mathrm{P}$ の移動の仕方について、例えば、硬貨を1回投げて表が出た場合について考える。このとき、点 $\mathrm{P}$ の座標は $(1,1)$ となる。これを図1のように、原点 $\mathrm{O}(0,0)$ と点 $(1,1)$ をまっすぐな矢印で結ぶ。このようにして点 $\mathrm{P}$ の移動の仕方を表す。

　以下において、図を使用する際には同じように考えることにする。

(i) 硬貨を3回投げ終えたとき、点 $\mathrm{P}$ の移動の仕方が条件

　$y_1\geqq -1$ かつ $y_2\geqq -1$ かつ $y_3\geqq -1$ $\cdots(*)$

を満たす確率を求めよう。

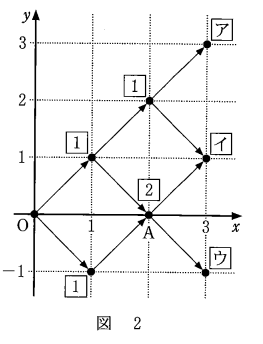
　条件 $(*)$ を満たす点 $\mathrm{P}$ の移動の仕方は図2のようになる。例えば点 $\mathrm{O}(0,0)$ から点 $\mathrm{A}(2,0)$ までの点 $\mathrm{P}$ の移動の仕方は、点 $\mathrm{O}(0,0)$ から点 $(1,1)$ まで移動したのち点 $\mathrm{A}(2,0)$ に移動する場合と、点 $\mathrm{O}(0,0)$ から点 $(1,-1)$ まで移動したのち点 $\mathrm{A}(2,0)$ に移動する場合のいずれかであるため、2通りある。このとき、この移動の仕方の総数である2を、四角囲みの中の数字で点 $\mathrm{A}(2,0)$ の近くに書く。図2における他の四角囲みの中の数字についても同様に考える。

　このように考えると、条件 $(*)$ を満たす点 $\mathrm{P}$ の移動の仕方のうち、点 $(3,3)$ に至る移動の仕方は $\myBox{ア}$ 通りあり、点 $(3,1)$ に至る移動の仕方は $\myBox{イ}$ 通りあり、点 $(3,-1)$ に至る移動の仕方は $\myBox{ウ}$ 通りある。

　よって、点 $\mathrm{P}$ の移動の仕方が条件 $(*)$ を満たすような硬貨の表裏の出方の総数は\[ \mybox{ア}+\mybox{イ}+\mybox{ウ} \]である。

　したがって、点 $\mathrm{P}$ の移動の仕方が条件 $(*)$ を満たす確率は\[ \frac{\mybox{ア}+\mybox{イ}+\mybox{ウ}}{2^3} \]として求めることができる。

(ii) 硬貨を4回投げるとする。このとき、(i)と同様に図を用いて考えよう。 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3\geqq 0$ かつ $y_4\geqq 0$ である確率は $\dfrac{\myBox{エ}}{\myBox{オ}}$ となる。また、 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3=1$ かつ $y_4\geqq 0$ である確率は $\dfrac{\myBox{カ}}{\myBox{キ}}$ となる。さらに、 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3\geqq 0$ かつ $y_4\geqq 0$ であったとき、 $y_3=1$ である条件付き確率は $\dfrac{\myBox{ク}}{\myBox{ケ}}$ となる。

(iii) 硬貨を4回投げ終えた時点で点 $\mathrm{P}$ の座標が $(4,2)$ であるとき、点 $(4,2)$ に至る移動の仕方によらず表の出る回数は $\myBox{コ}$ 回となり、裏の出る回数は $\left(4-\mybox{コ}\right)$ 回となる。

(2) 1個のさいころを繰り返し投げるとき、このさいころの目の出方に応じて、数直線上の点 $\mathrm{Q}$ が次の規則２に従って移動するものとする。

規則２

点 $\mathrm{Q}$ は原点 $\mathrm{O}$ を出発点とする。

点 $\mathrm{Q}$ の座標は、さいころを投げるごとに、3の倍数の目が出たら1だけ増加し、それ以外の目が出たら1だけ減少する。

(i) さいころを7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3である確率は $\dfrac{\myBox{サシ}}{\myBox{スセソ}}$ となる。

(ii) さいころを7回投げる間、点 $\mathrm{Q}$ の座標がつねに0以上3以下であり、かつ7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3である確率は $\dfrac{\myBox{タチ}}{\myBox{ツテトナ}}$ となる。

(iii) さいころを7回投げる間、点 $\mathrm{Q}$ の座標がつねに0以上3以下であり、かつ7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3であったとき、3回投げ終えた時点で点 $\mathrm{Q}$ の座標が1である条件付き確率は $\dfrac{\myBox{ニ}}{\myBox{ヌ}}$ となる。

考え方

経路の問題では、 $\mathrm{C}$ を使って解くことが多いですが、この問題では、 $\mathrm{C}$ を使わずに解くことが求められています。ただ、この方法も教科書などでは紹介されていることも多いです。(1)はそれほど難しくなく解いていくことができるでしょう。

(2)は(1)の応用ですが、コインではなくさいころです。このような場合にどうすればいいかは類題を解いたことがないと少し難しいかもしれません。計算も少し大変で、計算間違いしやすいです。さいころは7回ではなく5回にしてほしかったですね。

解答編

問題

(1) 1枚の硬貨を繰り返し投げるとき、この硬貨の表裏の出方に応じて、座標平面上の点 $\mathrm{P}$ が次の規則１に従って移動するものとする。

規則１

点 $\mathrm{P}$ は原点 $\mathrm{O}(0,0)$ を出発点とする。

点 $\mathrm{P}$ の $x$ 座標は、硬貨を投げるごとに $1$ だけ増加する。

点 $\mathrm{P}$ の $y$ 座標は、硬貨を投げるごとに、表が出たら $1$ だけ増加し、裏が出たら $1$ だけ減少する。

　また、点 $\mathrm{P}$ の座標を次の記号で表す。

記号
　硬貨を $k$ 回投げ終えた時点での点 $\mathrm{P}$ の座標 $(x,y)$ を $(k,y_k)$ で表す。

　座標平面上の点 $\mathrm{P}$ の移動の仕方について、例えば、硬貨を1回投げて表が出た場合について考える。このとき、点 $\mathrm{P}$ の座標は $(1,1)$ となる。これを図1のように、原点 $\mathrm{O}(0,0)$ と点 $(1,1)$ をまっすぐな矢印で結ぶ。このようにして点 $\mathrm{P}$ の移動の仕方を表す。

　以下において、図を使用する際には同じように考えることにする。

(i) 硬貨を3回投げ終えたとき、点 $\mathrm{P}$ の移動の仕方が条件

　$y_1\geqq -1$ かつ $y_2\geqq -1$ かつ $y_3\geqq -1$ $\cdots(*)$

を満たす確率を求めよう。

　条件 $(*)$ を満たす点 $\mathrm{P}$ の移動の仕方は図2のようになる。例えば点 $\mathrm{O}(0,0)$ から点 $\mathrm{A}(2,0)$ までの点 $\mathrm{P}$ の移動の仕方は、点 $\mathrm{O}(0,0)$ から点 $(1,1)$ まで移動したのち点 $\mathrm{A}(2,0)$ に移動する場合と、点 $\mathrm{O}(0,0)$ から点 $(1,-1)$ まで移動したのち点 $\mathrm{A}(2,0)$ に移動する場合のいずれかであるため、2通りある。このとき、この移動の仕方の総数である2を、四角囲みの中の数字で点 $\mathrm{A}(2,0)$ の近くに書く。図2における他の四角囲みの中の数字についても同様に考える。

　このように考えると、条件 $(*)$ を満たす点 $\mathrm{P}$ の移動の仕方のうち、点 $(3,3)$ に至る移動の仕方は $\myBox{ア}$ 通りあり、点 $(3,1)$ に至る移動の仕方は $\myBox{イ}$ 通りあり、点 $(3,-1)$ に至る移動の仕方は $\myBox{ウ}$ 通りある。

　よって、点 $\mathrm{P}$ の移動の仕方が条件 $(*)$ を満たすような硬貨の表裏の出方の総数は\[ \mybox{ア}+\mybox{イ}+\mybox{ウ} \]である。

　したがって、点 $\mathrm{P}$ の移動の仕方が条件 $(*)$ を満たす確率は\[ \frac{\mybox{ア}+\mybox{イ}+\mybox{ウ}}{2^3} \]として求めることができる。

解説

点 $(3,3)$ に移動できるのは、 $(2,2)$ に移動してから表が出る場合のみです。 $(2,2)$ に移動する方法が1通りなので、 $(3,3)$ に移動する方法も1通りです。

点 $(3,1)$ に移動する方法は、 $(2,2)$ への移動と $(2,0)$ への移動の仕方の総数を足して、 $1+2=3$ と求められます。

点 $(3,-1)$ に移動できるのは、 $(2,0)$ に移動してから次に裏が出る場合のみなので、2通りです。 $(2,-2)$ から移動するケースは条件を満たしていないので含めてはいけないので、 ${}_{3}\mathrm{C}_1$ などと計算してはいけないことに注意しましょう。

以上から、条件を満たす硬貨の出方の総数は6通りであり、確率は $\dfrac{6}{2^3}=\dfrac{3}{4}$ と求められます。

解答

ア：1 (1点)
イ：3 (1点)
ウ：2 (1点)

解答編　つづき

問題

(ii) 硬貨を4回投げるとする。このとき、(i)と同様に図を用いて考えよう。 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3\geqq 0$ かつ $y_4\geqq 0$ である確率は $\dfrac{\myBox{エ}}{\myBox{オ}}$ となる。また、 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3=1$ かつ $y_4\geqq 0$ である確率は $\dfrac{\myBox{カ}}{\myBox{キ}}$ となる。さらに、 $y_1\geqq 0$ かつ $y_2\geqq 0$ かつ $y_3\geqq 0$ かつ $y_4\geqq 0$ であったとき、 $y_3=1$ である条件付き確率は $\dfrac{\myBox{ク}}{\myBox{ケ}}$ となる。

解説

同じように図をかくと次のようになります。

どの点も $y$ 座標が $0$ 以上の場合、最終的には、 $(4,4)$, $(4,2)$, $(4,0)$ のどれかに移動します。それぞれ、$1,3,2$ 通りあるので、全部で $6$ 通りです。よって、 $y_1\geqq 0$, $y_2\geqq 0$, $y_3\geqq 0$, $y_4\geqq 0$ となる確率は\[ \frac{6}{2^4}=\frac{3}{8} \]となります。

$y_1\geqq 0$, $y_2\geqq 0$, $y_3=1$, $y_4\geqq 0$ となる移動は、 $(3,1)$ から $(4,2)$ と $(4,0)$ へ移動するときのみであり、その点までの移動の仕方はそれぞれ $2$ 通りずつあります。なので、このようになる確率は\[ \frac{4}{2^4}=\frac{1}{4} \]です。

これらから、$y_1\geqq 0$, $y_2\geqq 0$, $y_3\geqq 0$, $y_4\geqq 0$ であったときに $y_3=1$ である条件付き確率は\[ \frac{\frac{1}{4}}{\frac{3}{8}}=\frac{2}{3} \]となります。

解答

エオ：38 (3点)
カキ：14 (3点)
クケ：23 (2点)

解答編　つづき

問題

(iii) 硬貨を4回投げ終えた時点で点 $\mathrm{P}$ の座標が $(4,2)$ であるとき、点 $(4,2)$ に至る移動の仕方によらず表の出る回数は $\myBox{コ}$ 回となり、裏の出る回数は $\left(4-\mybox{コ}\right)$ 回となる。

解説

表が $p$ 回出るとすると、裏は $4-p$ 回出ることになります。表が出ると1増えて、裏が出ると1減って、結果が2になるので\[ p-(4-p)=2 \]が成り立ちます。これを解いて\[ p=3 \]と求められます。

解答

コ：3 (1点)

解答編　つづき

問題

(2) 1個のさいころを繰り返し投げるとき、このさいころの目の出方に応じて、数直線上の点 $\mathrm{Q}$ が次の規則２に従って移動するものとする。

規則２

点 $\mathrm{Q}$ は原点 $\mathrm{O}$ を出発点とする。

点 $\mathrm{Q}$ の座標は、さいころを投げるごとに、3の倍数の目が出たら1だけ増加し、それ以外の目が出たら1だけ減少する。

(i) さいころを7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3である確率は $\dfrac{\myBox{サシ}}{\myBox{スセソ}}$ となる。

解説

3の倍数の目が出た回数を $q$ 回だとすると、それ以外の目は $7-q$ 回出たことになります。なので、\[ q-(7-q)=3 \]が成り立つことから、 $q=5$ 、つまり、3の倍数は5回出たことがわかります。

7回中、3の倍数が出る5回はいつ起こるか、と考えれば、求める確率は
\begin{eqnarray} & & {}_{7}\mathrm{C}_5 \left(\frac{1}{3}\right)^5 \left(\frac{2}{3}\right)^2 \\[5pt] &=& \frac{7\cdot 6}{2} \cdot \frac{2^2}{3^7} \\[5pt] &=& \frac{7\cdot 2^2}{3^6} \\[5pt] &=& \frac{28}{729} \\[5pt] \end{eqnarray}となります。この問題は、途中の経路に制限がなく、3の倍数が出るタイミングは7回中いつでもいいので、 $\mathrm{C}$ を使って計算することができます。

解答

サシスセソ：28729 (2点)

解答編　つづき

問題

(ii) さいころを7回投げる間、点 $\mathrm{Q}$ の座標がつねに0以上3以下であり、かつ7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3である確率は $\dfrac{\myBox{タチ}}{\myBox{ツテトナ}}$ となる。

解説

経路に制約があるので、今回は $\mathrm{C}$ を使って解くのは難しいです。そのため、(1)と同じようにして考えます。

今回は数直線上の移動ですが、(1)と同じように、さいころを投げるたびに横に進んで平面上を移動すると考え、先ほどの図を使った方法で計算してみます。矢印や数字を囲む四角形は省略しています。

例えば、 $(3,1)$ への移動の仕方の総数は、

$(2,2)$ への移動の仕方の総数 $4$ に、 $4$ （3の倍数以外の総数）を掛けたもの
$(2,0)$ への移動の仕方の総数 $8$ に、 $2$ （3の倍数の総数）を掛けたもの

を足して $32$ と計算しています。上下への移動は $0$ 以上 $3$ 以下の場合のみを考えることから、条件を満たさないものは上の図からは省きます。また、最後には $(7,3)$ に移動しないといけないので、 $(7,1)$ や $(6,0)$ への移動も考える必要はありません。

右上への移動は $2$ 倍、右下への移動は $4$ 倍して足していくだけですが、計算は少し煩雑です。図のように必要なすべての点について計算すると、条件を満たす移動の総数は $4096$ 通りだとわかります。なので、確率は\[ \frac{4096}{6^7}=\frac{32}{2187} \]となります。

解答

タチツテトナ：322187 (3点)

解答編　つづき

問題

(iii) さいころを7回投げる間、点 $\mathrm{Q}$ の座標がつねに0以上3以下であり、かつ7回投げ終えた時点で点 $\mathrm{Q}$ の座標が3であったとき、3回投げ終えた時点で点 $\mathrm{Q}$ の座標が1である条件付き確率は $\dfrac{\myBox{ニ}}{\myBox{ヌ}}$ となる。