共通テスト 数学I・数学A 2023年度追試 第2問 [1] 解説

【必答問題】

問題編

問題

　高校１年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は１皿当たりの価格をいくらにするかを検討するためにアンケート調査を行い、１皿あたりの価格と売り上げ数の関係について次の表のように予測した。

1皿あたりの価格（円）	100	150	200	250	300
売り上げ数（皿）	1250	750	450	250	50

　この結果から太郎さんと花子さんは、１皿あたりの価格が $100$ 円以上 $300$ 円以下の範囲で、予測される利益（以下、利益）の最大値について考えることにした。

• 価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
• 散布図の点の並びは、１次関数のグラフのようには見えないね。２次関数のグラフみたいに見えるよ。
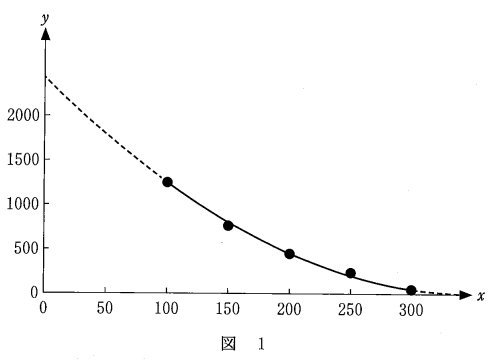
• 価格が $100$, $200$, $300$ のときの点を通る２次関数のグラフをかくと、図１のように価格が $150$, $250$ のときの点もそのグラフの近くにあるよ。
• 現実には、もっと複雑な関係なのだろうけど、１次関数と２次関数で比べると、２次関数で考えたほうがよいような気がするね。

　２次関数\[ y=ax^2+bx+c \quad \cdots ① \]のグラフは、3点 $(100,1250)$, $(200,450)$, $(300,50)$ を通るとする。このとき、 $b=\myBox{アイウ}$ である。

　二人は、１皿あたりの価格 $x$ と売り上げ数 $y$ の関係が①を満たしたときの、 $100\leqq x \leqq 300$ での利益の最大値 $M$ について考えることにした。

　１皿あたりの材料費は $80$ 円であり、材料費以外にかかる費用は $5000$ 円である。よって $x-80$ と売り上げ数の積から、 $5000$ を引いたものが利益となる。

　このとき、売り上げ数を①の右辺の２次式とすると、利益は $x$ の $\myBox{エ}$ 次式となる。一方で、売り上げ数として①の右辺の代わりに $x$ の $\myBox{オ}$ 次式を使えば、利益は $x$ の２次式となる。

• 利益が $\mybox{エ}$ 次式だと、今の私たちの知識では最大値 $M$ を正確に求めることができないね。
• ①の右辺の代わりに $\mybox{オ}$ 次式を使えば利益は２次式になるから、最大値を求められるよ。
• 現実の問題を考えるときには正確な答えが出せないことも多いから、自分の知識の範囲内で工夫しておおよその値を出すことには価値があると思うよ。
• 考えているのが利益だから、①の右辺の代わりの式は売り上げ数を少なく見積もった式を考えると手堅いね。
• 少なく見積もるということは、その関数のグラフは①のグラフより、下のほうにあるということだね。

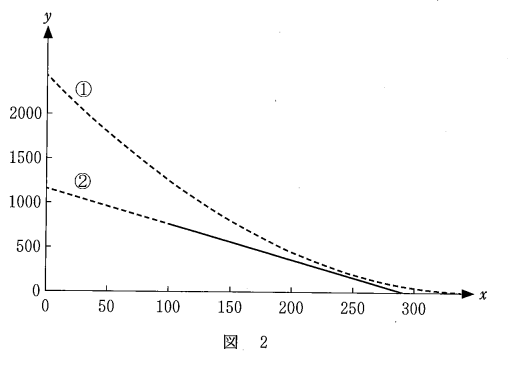
　１次関数\[ y=-4x+1160 \quad\cdots② \]を考える。このとき、①と②のグラフの位置関係は次の図の２のようになっている。

　①の右辺の代わりに②の右辺を使うと、売り上げ数を少なく見積もることになる。売り上げ数を②の右辺とした時の利益 $z$ は\[ z=-\myBox{カ}x^2+\myBox{キクケコ}x-97800 \]で与えられる。 $z$ が最大となる $x$ を $p$ とおくと、 $p=\myBox{サシス}$ であり、 $z$ の最大値は $39100$ である。

• 売り上げ数を少なく見積もった式は、各 $x$ について値が①より小さければよいので、色々な式が考えられるね。
• それらの式を①の右辺の代わりに使ったときの利益の最大値と、①の右辺から計算される利益の最大値 $M$ との関係はどうなるのかな。

　１次関数\[ y=-8x+1968 \quad\cdots③ \]を考える。売り上げ数を③の右辺としたときの利益は $x=163$ のときに最大となり、最大値は $50112$ となる。

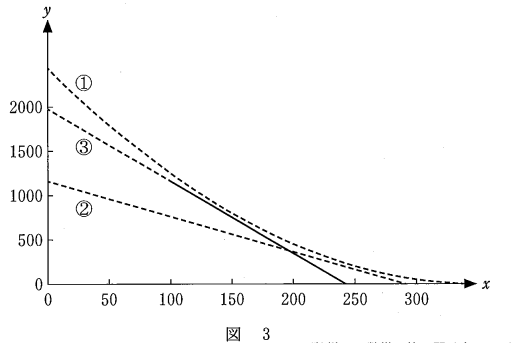
　また、①～③のグラフの位置関係は次の図３のようになっている。

　売り上げ数を①の右辺としたときの利益の記述として、次の 0 ～ 6 のうち、正しいものは $\dBox{セ}$ と $\dBox{ソ}$ である。

$\dbox{セ}$, $\dbox{ソ}$ の解答群（解答の順序は問わない。）

　0: 利益の最大値 $M$ は $39100$ である。
　1: 利益の最大値 $M$ は $50112$ である。
　2: 利益の最大値 $M$ は $\dfrac{39100+50112}{2}$ である。
　3: $x=163$ とすれば、利益は少なくとも $50112$ 以上となる。
　4: $x=p$ とすれば、利益は少なくとも $39100$ 以上となる。
　5: $x=163$ のときに利益は最大値 $M$ をとる。
　6: $x=p$ のときに利益は最大値 $M$ をとる。

　１次関数\[ y=-6x+1860 \quad\cdots ④ \]を考える。 $100\leqq x\leqq 300$ において、売り上げ数を④の右辺としたときの利益は $x=195$ のときに最大となり、最大値は $74350$ となる。

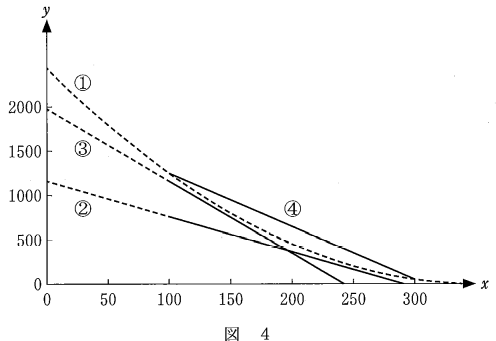
　また、①～④のグラフの位置関係は次の図４のようになっている。

　売り上げ数を①の右辺としたときの利益の最大値 $M$ についての記述として、次の 0 ～ 4 のうち、正しいものは $\dBox{タ}$ である。

$\dbox{タ}$ の解答群

　0: 利益の最大値 $M$ は $50112$ より小さい。
　1: 利益の最大値 $M$ は $50112$ である。
　2: 利益の最大値 $M$ は $50112$ より大きく $74350$ より小さい。
　3: 利益の最大値 $M$ は $74350$ である。
　4: 利益の最大値 $M$ は $74350$ より大きい。

考え方

問題文は長いですが、やっていることを理解しながら読み進めていくと、実は大したことはやっていないことがわかります。前半に少し計算がありますが、後半は問題文に書かれている数字が何を表しているかをよく考えながら解いていけば、計算するところはありません。

【必答問題】

解答編

問題

　高校１年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は１皿当たりの価格をいくらにするかを検討するためにアンケート調査を行い、１皿あたりの価格と売り上げ数の関係について次の表のように予測した。

1皿あたりの価格（円）	100	150	200	250	300
売り上げ数（皿）	1250	750	450	250	50

　この結果から太郎さんと花子さんは、１皿あたりの価格が $100$ 円以上 $300$ 円以下の範囲で、予測される利益（以下、利益）の最大値について考えることにした。

• 価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
• 散布図の点の並びは、１次関数のグラフのようには見えないね。２次関数のグラフみたいに見えるよ。
• 価格が $100$, $200$, $300$ のときの点を通る２次関数のグラフをかくと、図１のように価格が $150$, $250$ のときの点もそのグラフの近くにあるよ。
• 現実には、もっと複雑な関係なのだろうけど、１次関数と２次関数で比べると、２次関数で考えたほうがよいような気がするね。

　２次関数\[ y=ax^2+bx+c \quad \cdots ① \]のグラフは、3点 $(100,1250)$, $(200,450)$, $(300,50)$ を通るとする。このとき、 $b=\myBox{アイウ}$ である。

解説

$y=ax^2+bx+c$ のグラフが $(100,1250)$, $(200,450)$, $(300,50)$ を通ることから
\begin{eqnarray} 1250 &=& 10000a+100b+c \\[5pt] 450 &=& 40000a+200b+c \\[5pt] 50 &=& 90000a+300b+c \\[5pt] \end{eqnarray}の３つの等式が成り立ちます。３つ目から２つ目を引いた結果、２つ目から１つ目を引いた結果は、それぞれ、 \begin{eqnarray} -400 &=& 50000a+100b \\[5pt] -800 &=& 30000a+100b \\[5pt] \end{eqnarray}となります。この１つ目から２つ目を引くと \begin{eqnarray} 400 &=& 20000a \\[5pt] a = \frac{1}{50} \end{eqnarray}となります。これを使えば \begin{eqnarray} -400 &=& 50000 \cdot \frac{1}{50}+100b\\[5pt] -4 &=& 500 \cdot \frac{1}{50}+b\\[5pt] b &=& -4-10=-14 \end{eqnarray}と求められます。

解答

アイウ：-14 (3点)

解答編　つづき

問題

　二人は、１皿あたりの価格 $x$ と売り上げ数 $y$ の関係が①を満たしたときの、 $100\leqq x \leqq 300$ での利益の最大値 $M$ について考えることにした。

　１皿あたりの材料費は $80$ 円であり、材料費以外にかかる費用は $5000$ 円である。よって $x-80$ と売り上げ数の積から、 $5000$ を引いたものが利益となる。

　このとき、売り上げ数を①の右辺の２次式とすると、利益は $x$ の $\myBox{エ}$ 次式となる。一方で、売り上げ数として①の右辺の代わりに $x$ の $\myBox{オ}$ 次式を使えば、利益は $x$ の２次式となる。

解説

売り上げ数が $y=ax^2+bx+c$ と表せていたとすると、利益は\[ (ax^2+bx+c)(x-80)-5000 \]となります。 $a\ne 0$ だから、 $ax^3$ が一番大きな次数なので、この式は3次式です。一方、この計算結果が2次式となるには、売り上げ数の式は $x$ の1次式でないといけないことがわかります。

解答

エオ：31 (1点)

解答編　つづき

問題

• 利益が $\mybox{エ}$ 次式だと、今の私たちの知識では最大値 $M$ を正確に求めることができないね。
• ①の右辺の代わりに $\mybox{オ}$ 次式を使えば利益は２次式になるから、最大値を求められるよ。
• 現実の問題を考えるときには正確な答えが出せないことも多いから、自分の知識の範囲内で工夫しておおよその値を出すことには価値があると思うよ。
• 考えているのが利益だから、①の右辺の代わりの式は売り上げ数を少なく見積もった式を考えると手堅いね。
• 少なく見積もるということは、その関数のグラフは①のグラフより、下のほうにあるということだね。

　１次関数\[ y=-4x+1160 \quad\cdots② \]を考える。このとき、①と②のグラフの位置関係は次の図の２のようになっている。

　①の右辺の代わりに②の右辺を使うと、売り上げ数を少なく見積もることになる。売り上げ数を②の右辺とした時の利益 $z$ は\[ z=-\myBox{カ}x^2+\myBox{キクケコ}x-97800 \]で与えられる。 $z$ が最大となる $x$ を $p$ とおくと、 $p=\myBox{サシス}$ であり、 $z$ の最大値は $39100$ である。

解説

三次関数の最大値は数学Iの範囲では求められないので、なんとか二次関数の話にして近い値を考えてみよう、という流れです。

売り上げ数が $y=-4x+1160$ のとき、利益 $z$ は
\begin{eqnarray} z &=& (-4x+1160)(x-80)-5000 \\[5pt] &=& -4x^2+320x+1160x-92800-5000 \\[5pt] &=& -4x^2+1480x-97800 \\[5pt] \end{eqnarray}と表せます。これを変形すれば \begin{eqnarray} z &=& -4x^2+1480x-97800 \\[5pt] &=& -4(x^2-370x)-97800 \\[5pt] &=& -4(x-185)^2+4\cdot185^2-97800 \\[5pt] &=& -4(x-185)^2+136900-97800 \\[5pt] &=& -4(x-185)^2+39100 \\[5pt] \end{eqnarray} となるので、 $x=185$ のときに $z$ は最大値 $39100$ をとることがわかります。なので、 $p=185$ です。

解答

カキクケコ：41480 (2点)
サシス：185 (3点)

解答編　つづき

問題

• 売り上げ数を少なく見積もった式は、各 $x$ について値が①より小さければよいので、色々な式が考えられるね。
• それらの式を①の右辺の代わりに使ったときの利益の最大値と、①の右辺から計算される利益の最大値 $M$ との関係はどうなるのかな。

　１次関数\[ y=-8x+1968 \quad\cdots③ \]を考える。売り上げ数を③の右辺としたときの利益は $x=163$ のときに最大となり、最大値は $50112$ となる。

　また、①～③のグラフの位置関係は次の図３のようになっている。

　売り上げ数を①の右辺としたときの利益の記述として、次の 0 ～ 6 のうち、正しいものは $\dBox{セ}$ と $\dBox{ソ}$ である。

$\dbox{セ}$, $\dbox{ソ}$ の解答群（解答の順序は問わない。）

　0: 利益の最大値 $M$ は $39100$ である。
　1: 利益の最大値 $M$ は $50112$ である。
　2: 利益の最大値 $M$ は $\dfrac{39100+50112}{2}$ である。
　3: $x=163$ とすれば、利益は少なくとも $50112$ 以上となる。
　4: $x=p$ とすれば、利益は少なくとも $39100$ 以上となる。
　5: $x=163$ のときに利益は最大値 $M$ をとる。
　6: $x=p$ のときに利益は最大値 $M$ をとる。

解説

選択肢の 0, 1, 2 に出てくる、 $39100$ や $50112$ という数値は、売り上げ数を②や③で表したときの最大値なので、①とは直接は関係のない値です。また、選択肢 5, 6 の $163$ や $p$ という数値は、売り上げ数を②や③で表したときのものなので、①とは関係のない値です。たまたま同じになるかもしれませんが、ひとまず、保留にしておいたほうがいいでしょう。

選択肢3 について、①と③のグラフを見ると、①のほうが上にあるので、 $x=163$ のときの売り上げ数は①のほうが多くなります。価格が同じで売り上げ数が多いのだから、利益は③のときの利益である $50112$ 以上です。なので、これは正しいです。

選択肢4 について、①と②のグラフを見ると、①のほうが上にあるので、 $x=p$ のときの売り上げ数は①のほうが多くなります。先ほどと同様に、利益は③のときの利益である $39100$ 以上です。なので、これは正しいです。

ということで、3と4が答えです。

解答

セソ：34 (順不同。各2点)

解答編　つづき

問題

　１次関数\[ y=-6x+1860 \quad\cdots ④ \]を考える。 $100\leqq x\leqq 300$ において、売り上げ数を④の右辺としたときの利益は $x=195$ のときに最大となり、最大値は $74350$ となる。

　また、①～④のグラフの位置関係は次の図４のようになっている。

　売り上げ数を①の右辺としたときの利益の最大値 $M$ についての記述として、次の 0 ～ 4 のうち、正しいものは $\dBox{タ}$ である。

$\dbox{タ}$ の解答群

　0: 利益の最大値 $M$ は $50112$ より小さい。
　1: 利益の最大値 $M$ は $50112$ である。
　2: 利益の最大値 $M$ は $50112$ より大きく $74350$ より小さい。
　3: 利益の最大値 $M$ は $74350$ である。
　4: 利益の最大値 $M$ は $74350$ より大きい。

解説

$x=q$ のときに最大値 $M$ をとるとします。このとき、①と④のグラフを見ると、①のほうが下にあるので、 $x=q$ のときの売り上げ数は①のほうが少なくなります。よって、$x=q$ を①に代入して $x-80$ を掛けて $5000$ を引いたものは、④に同じように代入して計算して得られる値 $74350$ より小さくなります。

よって、先ほどの「セ・ソ」の内容と合わせると、 $M$ は $50112$ より大きく、 $74350$ より小さいことがわかります。

解答

タ：2 (2点)