京都大学 理学部特色入試 2024年度 第3問 解説
(2023年11月に行われた特色入試の問題です。)
問題編
問題
座標平面上の円 $D_1:x^2+y^2=64$ と円 $D_2:x^2+(y-4)^2=9$ に関して、以下の設問に答えよ。
(1) 座標平面上の3点 $(0,8)$, $(3\sqrt{7},1)$, $(-3\sqrt{7},1)$ を頂点とする三角形の外接円は $D_1$ であり、内接円は $D_2$ であることを示せ。
(2) $D_1$ が外接円であり、さらに $D_2$ が内接円である任意の三角形 $\triangle \mathrm{ABC}$ に対して、実数 $\alpha,\beta,\gamma$ を
\begin{eqnarray} \alpha &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{BC}, \\[5pt] \beta &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{CA}, \\[5pt] \gamma &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{AB}, \\[5pt] \end{eqnarray}と定める。このとき $\alpha\beta+\beta\gamma+\gamma\alpha=105$ が成り立つことを示せ。
考え方
(1)はいいとして、問題は(2)です。式の形から何かの気配を読み取りましょう。証明には計算力も必要で、難しいです。
解答編
問題
座標平面上の円 $D_1:x^2+y^2=64$ と円 $D_2:x^2+(y-4)^2=9$ に関して、以下の設問に答えよ。
(1) 座標平面上の3点 $(0,8)$, $(3\sqrt{7},1)$, $(-3\sqrt{7},1)$ を頂点とする三角形の外接円は $D_1$ であり、内接円は $D_2$ であることを示せ。
(2) $D_1$ が外接円であり、さらに $D_2$ が内接円である任意の三角形 $\triangle \mathrm{ABC}$ に対して、実数 $\alpha,\beta,\gamma$ を
\begin{eqnarray} \alpha &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{BC}, \\[5pt] \beta &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{CA}, \\[5pt] \gamma &=& \dfrac{\mathrm{AB+BC+CA}}{2} - \mathrm{AB}, \\[5pt] \end{eqnarray}と定める。このとき $\alpha\beta+\beta\gamma+\gamma\alpha=105$ が成り立つことを示せ。
解答
(1)
$\mathrm{A}(0,8)$, $\mathrm{B}(3\sqrt{7},1)$, $\mathrm{C}(-3\sqrt{7},1)$ とする。
$0^2+8^2=64$, $(3\sqrt{7})^2+1^2=(-3\sqrt{7})^2+1^2=64$ なので、3点 $\mathrm{A,B,C}$ は $D_1$ 上にあるから、 $\triangle \mathrm{ABC}$ の外接円は $D_1$ であることがわかる。
$\triangle \mathrm{ABC}$ の内心を $\mathrm{I}$ とすると、 $\mathrm{I}$ は $y$ 軸上にある。また、 $\mathrm{M}(0,1)$ とすると、これは辺 $\mathrm{BC}$ と内接円との接点となる。
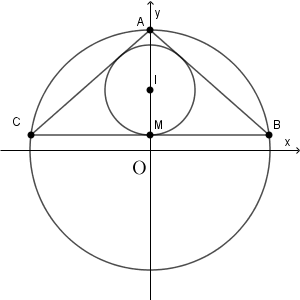
$\mathrm{AB}=\sqrt{(3\sqrt{7})^2+7^2}=4\sqrt{7}$ で $\mathrm{MB}=3\sqrt{7}$ なので、 $\mathrm{AI:IM}=\mathrm{BA:BM}=4:3$ だから $\mathrm{I}(0,4)$ だとわかる。
また、 $\mathrm{IM}=3$ なので、 $\triangle \mathrm{ABC}$ の内接円は $D_2$ であることがわかる。
(終)
(2)
\begin{eqnarray}
& &
\alpha+\beta+\gamma \\[5pt]
&=&
\frac{3(\mathrm{AB+BC+CA})}{2}-(\mathrm{AB+BC+CA}) \\[5pt]
&=&
\frac{\mathrm{AB+BC+CA}}{2}
\end{eqnarray}なので、 $\triangle \mathrm{ABC}$ の面積を $S$ とすると、ヘロンの公式から
\begin{eqnarray}
S=\sqrt{\alpha\beta\gamma(\alpha+\beta+\gamma)}
\end{eqnarray}がわかる。
また、内接円の半径を $r$ とおくと
\begin{eqnarray}
S &=& \dfrac{r}{2} (\mathrm{AB+BC+CA}) \\[5pt]
&=& \dfrac{r}{2} \cdot 2(\alpha+\beta+\gamma) \\[5pt]
&=& 3(\alpha+\beta+\gamma) \\[5pt]
\end{eqnarray}が得られる。この2つの式から
\begin{eqnarray}
\sqrt{\alpha\beta\gamma(\alpha+\beta+\gamma)} &=& 3(\alpha+\beta+\gamma) \\[5pt]
\alpha\beta\gamma(\alpha+\beta+\gamma) &=& 9(\alpha+\beta+\gamma)^2 \\[5pt]
\alpha\beta\gamma &=& 9(\alpha+\beta+\gamma) \\[5pt]
\end{eqnarray}が得られる。
さらに、外接円の半径を $R$ とおくと、 $\alpha+\beta=\mathrm{AB}$, $\beta+\gamma=\mathrm{BC}$, $\gamma+\alpha=\mathrm{CA}$ となることを使えば、
\begin{eqnarray}
S &=& \dfrac{\mathrm{AB\cdot BC}}{2} \sin \angle \mathrm{ABC} \\[5pt]
&=& \dfrac{\mathrm{AB\cdot BC}}{2} \cdot\frac{\mathrm{CA}}{2R} \\[5pt]
&=& \dfrac{(\alpha+\beta)(\beta+\gamma)(\gamma+\alpha)}{32}
\end{eqnarray}となる。
よって、
\begin{eqnarray}
& & (\alpha+\beta)(\beta+\gamma)(\gamma+\alpha) = 32S \\[5pt]
& & (\alpha+\beta)(\beta+\gamma)(\gamma+\alpha)+\alpha\beta\gamma = 32\cdot 3(\alpha+\beta+\gamma) +9(\alpha+\beta+\gamma) \\[5pt]
& & (\alpha+\beta+\gamma)(\alpha\beta+\beta\gamma+\gamma\alpha) = 105(\alpha+\beta+\gamma) \\[5pt]
& & \alpha\beta+\beta\gamma+\gamma\alpha= 105 \\[5pt]
\end{eqnarray}が成り立つ。
(終)





