京都大学 理学部特色入試 2024年度 第2問 解説
(2023年11月に行われた特色入試の問題です。)
問題編
問題
$x^{100}-3x^{10}-2x-1=0$ を満たす実数 $x$ の個数を求めよ。
考え方
$100$ 次方程式はなかなかインパクトがありますが、解いていくと、しっかりと考えられている次数・係数だとわかります。なかなかきわどい値になっています。
$-1\lt x\lt 0$ のところを詳しく見る必要がありますが、工夫せずにそのまま計算すると破綻してしまいます。関数の特徴をよく見て、うまく計算するようにしましょう。
解答編
問題
$x^{100}-3x^{10}-2x-1=0$ を満たす実数 $x$ の個数を求めよ。
解答
$f(x)=x^{100}-3x^{10}-2x-1$ とおく。 $f'(x)=100x^{99}-30x^9-2$ である。
(i) $x\geqq 1$ のとき
$f(1)=1-3-2-1=-5$ であり、 $\displaystyle \lim_{x\to\infty} f(x)=\infty$ である。また、
\begin{eqnarray}
f'(x)
&=&
10x^9 (10x^{90}-3) -2 \\[5pt]
&\geqq&
10 (10-3) -2 \gt 0 \\[5pt]
\end{eqnarray}なので、狭義単調増加であるから、この範囲で $f(x)=0$ は実数解を1つもつ。
(ii) $x\leqq -1$ のとき
$f(-1)=1-3+2-1=-1$ であり、 $\displaystyle \lim_{x\to-\infty} f(x)=\infty$ である。また、
\begin{eqnarray}
f'(x)
&=&
10x^9 (10x^{90}-3) -2 \\[5pt]
&\leqq&
-10 (10-3) -2 \lt 0 \\[5pt]
\end{eqnarray}なので、狭義単調減少であるから、この範囲で $f(x)=0$ は実数解を1つもつ。
(iii) $0\leqq x\lt 1$ のとき
\begin{eqnarray} f(x) &=& x^{100}-3x^{10}-2x-1 \\[5pt] &\lt& 1-0-0-1 = 0 \\[5pt] \end{eqnarray}なので、この範囲で $f(x)=0$ は実数解をもたない。(iv) $-1\lt x\lt 0$ のとき
$f'(x)=100x^{99}-30x^9-2$ なので
\begin{eqnarray}
f^{\prime\prime}(x)
&=&
9900x^{98}-270x^{8} \\[5pt]
&=&
90x^8(110x^{90}-3) \\[5pt]
\end{eqnarray}なので、 $-1\lt x\lt 0$ で $f^{\prime\prime}(x)=0$ となるのは $x=-\sqrt[90]{\dfrac{3}{110}}$ のときのみ。よって、 $f'(x)$ の増減表は次のようになる。
\begin{array}{c|ccccc}
x & -1 & \cdots & -\sqrt[90]{\dfrac{3}{110}} & \cdots & 0 \\
\hline
f^{\prime\prime}(x) & & + & 0 & - & \\
\hline
f'(x) & & \nearrow & & \searrow &
\end{array}
ここで、 $f'(0)=-2\lt 0$, $f'(-1)=-100+30-2\lt 0$ であり、 $f'(x)=100x^{99}-30x^9-2=10x^9 (10x^{90}-3) -2$ に $x=-\sqrt[90]{\dfrac{3}{110}}$ を代入すると
\begin{eqnarray}
& &
-10 \sqrt[10]{\frac{3}{110}} \left(10\cdot \frac{3}{110}-3\right)-2 \\[5pt]
&=&
-10 \sqrt[10]{\frac{3}{110}} \cdot \frac{-30}{11}-2 \\[5pt]
&=&
\frac{300}{11} \sqrt[10]{\frac{3}{110}} -2 \\[5pt]
&\gt&
\frac{300}{11} \cdot\frac{1}{10} -2 \\[5pt]
&\gt&
0
\end{eqnarray}がわかる。なお、途中で $\dfrac{3}{110}\gt\dfrac{1}{10^{10}}$ を用いている。
これらの値と増減表から、 $-1\lt x\lt 0$ の範囲で $f'(x)=0$ は2つの実数解をもつ。これらを $\alpha,\beta$ とおく(ただし、 $\alpha\lt \beta$ )。このとき、 $f(x)$ の増減表は次のようになる。
\begin{array}{c|ccccc} x & -1 & \cdots & \alpha & \cdots & \beta & \cdots & 0 \\ \hline f'(x) & & - & 0 & + & 0 & - & \\ \hline f(x) & & \searrow & & \nearrow & & \searrow & \end{array}$f(-1)=-1$, $f(0)=-1$ なので、 $-1\lt x\lt 0$ の範囲で $f(x)=0$ の実数解は高々2個である。
ここで、 $g(x)=3x^{10}+2x$ とおくと、 $g'(x)=30x^9+2$ なので、 $-1\lt x\lt 0$ の範囲で $g'(x)=0$ の実数解は $x=-\sqrt[9]{\dfrac{1}{15}}$ である。この値を $f(x)=x^{100}-3x^{10}-2x-1$ に代入すると
\begin{eqnarray}
& &
f\left( -\sqrt[9]{\dfrac{1}{15}} \right) \\[5pt]
&=&
\left(\frac{1}{15}\right)^{11} \sqrt[9]{\dfrac{1}{15}} -3\cdot\frac{1}{15} \sqrt[9]{\dfrac{1}{15}} +2\sqrt[9]{\dfrac{1}{15}}-1 \\[5pt]
&\gt&
\left(-\frac{1}{5}+2\right) \sqrt[9]{\dfrac{1}{15}} -1 \\[5pt]
&=&
\frac{9}{5} \sqrt[9]{\dfrac{1}{15}} -1 \\[5pt]
&=&
\sqrt[9]{\dfrac{1.8^9}{15}} -1 \\[5pt]
&\gt&
\sqrt[9]{\dfrac{3\cdot 3\cdot 3}{15}} -1 \\[5pt]
&\gt&
0
\end{eqnarray}となることがわかる。
\begin{array}{c|ccccc}
x & -1 & \cdots & \alpha & \cdots & \beta & \cdots & 0 \\
\hline
f'(x) & & - & 0 & + & 0 & - & \\
\hline
f(x) & -1 & \searrow & & \nearrow & & \searrow & -1
\end{array}
$-1\lt x\lt 0$ で $f(x)\gt 0$ となる $x$ が存在するため、上の増減表から $f(\beta)\gt 0$ であり、この範囲で $f(x)=0$ は実数解を2つもつことがわかる。
(i)~(iv) より、$f(x)=0$ を満たす実数 $x$ の個数は $4$ …(答)
解説
$f(x)=x^{100}-3x^{10}-2x-1$ を $y=x^{100}-1$ と $y=3x^{10}+2x$ に分解してグラフにすると、次のようになります。交点の $x$ 座標と $f(x)=0$ の実数解が対応します。
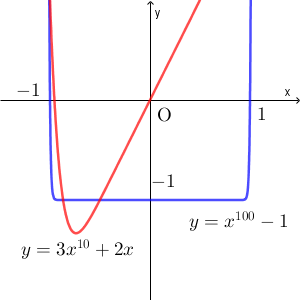
上の解答では、 $-1\lt x\lt 0$ の範囲で、 $f'(x)=0$ には2つの実数解が存在することを見ました。これを $\alpha,\beta$ とおいたのですが、普通は $f(\beta)$ (極大値)の符号がどうなるかを考える流れになります。
しかし、 $\beta$ の具体的な値はわからないですし、 $99$ 次方程式を解くのも非現実的です。ただ、よく考えれば、 $\beta$ のまわりでは $y=x^{100}-1$ の値はほとんど変化しないことがわかります。なので、 $y=f(x)$ の変化は、 $y=3x^{10}+2x$ の変化を調べるとだいたいわかるので、 $x=-\sqrt[9]{\dfrac{1}{15}}$ を代入して値を調べる、という手法をとっています。
もちろん、$\beta$ に近い別の値を入れる方法もあります。 $f(x)\gt 0$ となる値であればなんでもいいのですが、手計算で適切な値を見つけるのは少し難しいかもしれません。





