京都大学 理学部特色入試 2016年度 第4問 解説
(2015年11月に行われた特色入試の問題です。2016年に行われた特色入試の問題はこちら)
問題編
問題
以下の条件をすべて満たす数列 $\{x_n\}$, $\{y_n\}$ は存在するか。
(条件1)すべての自然数 n に対して、 $x_n$ および $y_n$ は自然数である。
(条件2)すべての自然数 n, m に対して、不等式\[ |n-m| \leqq 100|x_n-x_m| +100|y_n-y_m| +100 \]が成立する。
(条件3)どのような自然数 a, b に対しても、自然数 n を適切に選べば不等式\[ |a-x_n|+|b-y_n|\leqq 100 \]が成立する。
考え方
イメージでいうと、条件2は「だいぶ先の方で、すごく散らばっている」という条件であり、条件3は「ぎっしり詰まっている」条件です。なので、この2つを同時に満たすのは難しいんじゃないか、と予想できます。
実際、n をすごく大きくしていくと、条件2と条件3を同時に満たすのが不可能になってきます。このことを解答にしていきます。書きにくいですが。
解答編
問題
以下の条件をすべて満たす数列 $\{x_n\}$, $\{y_n\}$ は存在するか。
(条件1)すべての自然数 n に対して、 $x_n$ および $y_n$ は自然数である。
(条件2)すべての自然数 n, m に対して、不等式\[ |n-m| \leqq 100|x_n-x_m| +100|y_n-y_m| +100 \]が成立する。
(条件3)どのような自然数 a, b に対しても、自然数 n を適切に選べば不等式\[ |a-x_n|+|b-y_n|\leqq 100 \]が成立する。
解答
数列 $\{x_n\}$, $\{y_n\}$ が条件1と条件2を満たすとする。
k を自然数とする。 $m=1$, $n \gt 100k+10101$ のときも条件2は成り立つ。条件2の左辺は\[|n-m|\gt 100k+10100\]である。よって、次が成り立つ。
\begin{eqnarray}
100k+10100 & \lt & 100|x_n-x_1| +100|y_n-y_1| +100 \\
k+100 & \lt & |x_n-x_1| +|y_n-y_1| \quad \cdots (1)
\end{eqnarray}
ここで、4点 $(x_1+k+100,y_1)$, $(x_1,y_1+k+100)$, $(x_1-k-100,y_1)$, $(x_1,y_1-k-100)$ を頂点とする四角形 $S_k$ と、4点 $(x_1+k,y_1)$, $(x_1,y_1+k)$, $(x_1-k,y_1)$, $(x_1,y_1-k)$ を頂点とする四角形 $T_k$ を考える(ともに、境界線上の点を含む)。
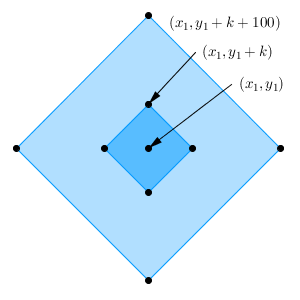
四角形 $S_k$ 内の点 $(x,y)$ は、 $|x-x_1| +|y-y_1| \leqq k+100$ を満たす。つまり、(1)から $n \gt 100k+10101$ のときは、点 $(x_n,y_n)$ はこの四角形 $S_k$ の中に入らないことがわかる。よって、 $n \gt 100k+10101$ のときは、四角形 $T_k$ 内の格子点 $(a,b)$ に対して、 $|a-x_n|+|b-y_n|\gt 100$ となる。
このことから、 $T_k$ 内の格子点 $(a,b)$ に対して、 $|a-x_n|+|b-y_n|\leqq 100$ が成り立つとすれば、 $n \leqq 100k+10101$ である。また、格子点 $(x,y)$ に対して、 $|a-x|+|b-y|\leqq 100$ を満たす自然数 a, b の組は、高々 $201\times 201$ 個である。つまり、各 $(x_n,y_n)$ に対し、 $|a-x_n|+|b-y_n|\leqq 100$ を満たす格子点 $(a,b)$ を求め、四角形 $T_k$ に含まれる点だけを数えると、その個数は最大でも\[ (100k+10101)\times 201^2 \]である。
ここで、 $(x_1+k,y_1)$, $(x_1,y_1+k)$, $(x_1,y_1)$ を結んでできる三角形に含まれる格子点は、 x 座標と y 座標がともに正であり、その点の数は、 $\displaystyle \frac{1}{2}(k+1)(k+2)$ なので、条件3が成り立つには、少なくともすべての k に対して\[ \frac{1}{2}(k+1)(k+2) \leqq (100k+10101)\times 201^2 \]が成り立たないといけない。しかし、 k が十分大きいとき(例えば、 $k=10^8$ など)とすれば、成り立たない。
よって、条件を満たす数列は存在しない。
解説
条件2があるので、n が大きいときは、点 $(x_n,y_n)$ は上の図の外側の四角形 $S_k$ より外にいることになります。また、条件3は、内側の四角形 $T_k$ の中に $(x_n,y_n)$ がぎっしり詰まってないといけないということです。しかし、四角形の大きさは2乗のスピードで大きくなるのに対し、覆える点の数は1乗のスピードでしか増えないので、覆いきれない、ということで矛盾が出てきます。
条件3は、「どのような a, b に対しても適切な n が存在する」という内容ですが、上の解答では、これを「各 n に対して条件を満たす a, b を集めていけば全体になる」というように視点を変えています。条件3が成り立つなら、 $T_k$ 内の点をすべて覆えるはず、と考えているわけですね。





