京都大学 理系 2015年度 第4問 解説
問題編
問題
一辺の長さが1の正四面体ABCD において、P を辺AB の中点とし、点Q が辺AC 上を動くとする。このとき、$\cos \angle\mathrm{PDQ}$ の最大値を求めよ。
考え方
AQ の長さを t などとおいて、$\cos \angle\mathrm{PDQ}$ を求めます。いろいろやり方はあると思いますが、ここでは余弦定理を繰り返し使う方法で出してみます。60° がたくさん出てくるので、そんなに苦労せずに $\cos$の値は求められます。
最大値を求めるときに、分母にルートが出てくるので大変です。しかし、そのまま微分する必要はなく、2乗した時の最大値を求めればOKです。
解答編
問題
一辺の長さが1の正四面体ABCD において、P を辺AB の中点とし、点Q が辺AC 上を動くとする。このとき、$\cos \angle\mathrm{PDQ}$ の最大値を求めよ。
解答
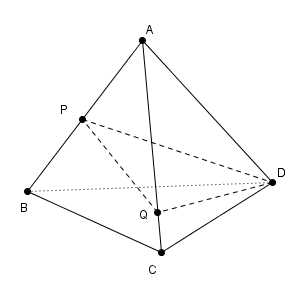
AQ の長さを t とする($0 \leqq t \leqq 1$)。
P は AB の中点なので、$\mathrm{ DP }=\dfrac{\sqrt{3} }{2}$ である。三角形DQA に対して余弦定理を用いると、
\begin{eqnarray}
\cos \angle \mathrm{QAD} &=& \frac{\mathrm{QA}^2+\mathrm{AD}^2-\mathrm{QD}^2}{2\mathrm{QA}\cdot \mathrm{AD}} \\[5pt]
\frac{1}{2} &=& \frac{t^2+1-\mathrm{QD}^2}{2t} \\[5pt]
\mathrm{QD}^2 &=& t^2 - t + 1 \\[5pt]
\end{eqnarray}
となる。
ここで、$t^2 - t + 1=\left(t-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\geqq 0$ なので、\[ \mathrm{QD} = \sqrt{t^2 - t + 1} \]となる。
また、三角形$\mathrm{ APQ }$ に対して余弦定理を用いると
\begin{eqnarray}
\cos \angle \mathrm{QAP} &=& \frac{\mathrm{QA}^2+\mathrm{AP}^2-\mathrm{QP}^2}{2\mathrm{QA}\cdot \mathrm{AP}} \\[5pt]
\frac{1}{2} &=& \frac{t^2+\frac{1}{4}-\mathrm{QP}^2}{t} \\[5pt]
\mathrm{QP}^2 &=& t^2 - \frac{1}{2}t + \frac{1}{4} \\[5pt]
\end{eqnarray}となる。
よって、三角形 $\mathrm{PDQ}$ に対して余弦定理を用いると、
\begin{eqnarray}
\cos \angle \mathrm{PDQ}
&=& \frac{\mathrm{PD}^2+\mathrm{DQ}^2-\mathrm{PQ}^2}{2 \mathrm{PD}\cdot \mathrm{DQ}} \\[5pt]
&=&
\frac{ \left( \frac{\sqrt{3} }{2} \right)^2 + (t^2 - t + 1) - (t^2 - \frac{1}{2}t + \frac{1}{4}) }{2 \frac{\sqrt{3} }{2} \sqrt{t^2 - t + 1} } \\[5pt]
&=&
\frac{ -\frac{1}{2}t + \frac{3}{2} }{\sqrt{3} \sqrt{t^2 - t + 1} } \\[5pt]
&=&
\frac{ -t + 3 }{2 \sqrt{3} \sqrt{t^2 - t + 1} } \ \ \cdots (1)
\end{eqnarray}が得られる。
ここで、$0 \leqq t \leqq 1$ のとき、(1)は正なので、$\cos \angle \mathrm{PDQ}$ を最大にする $t$ と $\cos^2 \angle \mathrm{PDQ}$ を最大にする $t$ は同じである。$f(t)=\cos^2 \angle \mathrm{PDQ}$ とすると
\begin{eqnarray}
f(t)
&=&
\frac{ t^2-6t+9 }{12 (t^2 - t + 1) } \\[5pt]
&=&
\frac{1}{12} + \frac{ -5t+8 }{12 (t^2 - t + 1) } \\[5pt]
\end{eqnarray}なので、
\begin{eqnarray}
f'(t)
&=&
\frac{ 1 }{12}\frac{ -5(t^2 - t + 1) - (-5t+8)(2t-1) }{ (t^2 - t + 1)^2 } \\[5pt]
&=&
\frac{ 1 }{12}\frac{ -5t^2 + 5t -5 + 10t^2 - 21t +8 }{ (t^2 - t + 1)^2 } \\[5pt]
&=&
\frac{ 1 }{12}\frac{ 5t^2 -16t +3 }{ (t^2 - t + 1)^2 } \\[5pt]
&=&
\frac{ 1 }{12}\frac{ (5t-1)(t-3) }{ (t^2 - t + 1)^2 }
\end{eqnarray}
となる。
この式から、$f'(t)=0$ のとき、$t=\dfrac{1}{5}, 3$ となることがわかるので、増減表は次の通りとなる。
\begin{array}{c|ccccc}
t & 0 & \cdots & \frac{1}{5} & \cdots & 1 \\
\hline
f'(t) & & + & 0 & - & \\
\hline
f(t) & & \nearrow & & \searrow &
\end{array}
よって、$f(t)$ は $t=\dfrac{1}{5}$ のときに最大となる。このことから、$\cos\angle \mathrm{PDQ}$ の最大値は、(1)に $t=\dfrac{1}{5}$ を代入して
\begin{eqnarray}
\frac{ -\frac{1}{5} + 3 }{2 \sqrt{3} \sqrt{\left(\frac{1}{5}\right)^2 - \frac{1}{5} + 1} }
&=&
\frac{ -1 + 15 }{2 \sqrt{3} \sqrt{1 - 5 + 25} } \\[5pt]
&=&
\frac{ 14 }{2 \sqrt{3} \sqrt{21} } \\[5pt]
&=&
\frac{ \sqrt{7} }{ 3 }
\end{eqnarray}
となる。
(答) $\dfrac{ \sqrt{7} }{ 3 }$
解説
上の解答では $\cos$ を求めるときに余弦定理を使いましたが、ベクトルの内積を用いる方法でもいいですね。つまり、\[
\overrightarrow{\mathrm{DP}} \cdot \overrightarrow{\mathrm{DQ}} = |\overrightarrow{\mathrm{DP}}||\overrightarrow{\mathrm{DQ}}| \cos \angle PDQ
\]
を使う方法です。$|\overrightarrow{\mathrm{DP}}|=\dfrac{\sqrt{3} }{2}$ はいいとして、他の項目は次のようにすれば求められます。
<別解($\cos \angle \mathrm{PDQ}$ を $t$ で表現する部分のみ)>
$\overrightarrow{\mathrm{DA}},\overrightarrow{\mathrm{DB}},\overrightarrow{\mathrm{DC}}$ をそれぞれ $\vec{a}, \vec{b}, \vec{c}$ と書く。
\begin{eqnarray}
& &
\overrightarrow{\mathrm{DP}} \cdot \overrightarrow{\mathrm{DQ}} \\[5pt]
&=&
\left( \frac{1}{2}\vec{a} + \frac{1}{2}\vec{b} \right) \cdot \{ (1-t)\vec{a} + t\vec{c} \} \\[5pt]
&=&
\frac{1}{2}\{ (1-t) |\vec{a}|^2+ t \vec{a}\cdot \vec{c} + (1-t)\vec{a}\cdot \vec{b} + t \vec{b}\cdot \vec{c} \} \\[5pt]
&=&
\frac{1}{2} \left( 1-t + \frac{t}{2} + \frac{1-t}{2} + \frac{t}{2} \right) \\[5pt]
&=&
\frac{-t+3}{4}
\end{eqnarray}
であり、
\begin{eqnarray}
|\overrightarrow{\mathrm{DQ}}|^2
&=&
|(1-t)\vec{a} + t\vec{c}|^2 \\[5pt]
&=&
(1-t)^2|\vec{a}|^2 + 2t(1-t)\vec{a}\cdot \vec{c} + t^2|\vec{c}|^2 \\[5pt]
&=&
(1-2t+t^2) + (-t^2+t) + t^2 \\[5pt]
&=&
t^2-t+1
\end{eqnarray}
なので、
\begin{eqnarray}
\cos \angle \mathrm{PDQ} &=& \frac{\overrightarrow{\mathrm{DP}} \cdot \overrightarrow{\mathrm{DQ}} }{|\overrightarrow{\mathrm{DP}}||\overrightarrow{\mathrm{DQ}}|} \\[5pt]
&=&
\frac{\frac{-t+3}{4} }{\frac{\sqrt{3} }{2} \sqrt{t^2-t+1} } \\[5pt]
&=&
\frac{-t+3}{2\sqrt{3} \sqrt{t^2-t+1} }
\end{eqnarray}
となる。
(別解終)
ここから先は同じですね。どちらでも解けるようになっておくのがいいでしょう。





